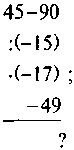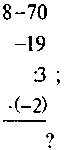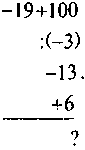Рівняння. Основні властивості рівнянь
Урок № 97
Тема. Рівняння. Основні властивості рівнянь
Мета: закріпити знання учнів про властивості (рівносильність) рівнянь; вдосконалити вміння розв’язувати рівняння із застосуванням властивостей рівносильності та інших властивостей (перетворення) виразів.
Тип уроку: застосування знань, умінь та навичок.
Хід уроку
I. Організаційний момент
II. Перевірка домашнього завдання
Гра “Знайди помилку”. Учитель заздалегідь записує розв’язання кількох типових рівнянь з домашнього завдання, “припустившись”
Усні вправи.
1. Обчисліть:
А) |
| Б) |
| В) |
|
2. Спростіть вираз:
А) 2(х – 3); б) -2(х – 3); в) -0,2(х + 0,3); г) 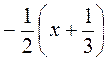 ; д)2х + 3х; е) -2х – 3х; ж) 2х – 3х; з) -2х + 3х, к) -2х + 3 – х.
; д)2х + 3х; е) -2х – 3х; ж) 2х – 3х; з) -2х + 3х, к) -2х + 3 – х.
3. Чи с серед наведених рівнянь пари, що мають рівні (однакові) корені?
А) 3х – 2 = х + 4;
Б) 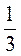 Х – 1 = x;
Х – 1 = x;
В) 3х – х = -2 + 4;
Г) х – 3 = 3х;
Д) 3х – х = 4 + 2;
Е) х – 1 = х;
Ж) 2(х + 3) = -2;
З) х + 3 = -2;
К) х + 3 = -1.
III. Відтворення знань
Запитання до класу
1. Обидві частини рівняння помножили на число, що не дорівнює 0. Чи змінились корені цього рівняння? Наведіть приклад.
2. Обидві частини рівняння поділили на одне й те саме число, що не дорівнює 0. Чи змінились корені рівняння? Наведіть приклад.
3. Сформулюйте правило переносу доданків з однієї частини рівняння в іншу. Наведіть приклад.
IV. Мотивація навчальної діяльності
@ Головна мета уроку – завершити формування уявлення про алгоритм розв’язування лінійних рівнянь з однією змінною (хоча поняття лінійного рівняння ми розглядатимемо трохи пізніше). Формування цього уявлення ми робимо, спираючись на приклади (розв’язування рівнянь), але, перш ніж наводити приклади, бажано, щоб учитель наголосив на тому, що під час розв’язування різноманітних на перший погляд (учнів) рівнянь ми використовуємо певні схеми (алгоритми), тобто вивчені нами властивості застосовуємо в певному порядку. На уроці ми встановлюємо цей порядок.
V. Систематизація знань
Розв’яжіть рівняння:
А) 6х – 12 = 5х + 4;
Б) 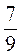 Х + 3 =
Х + 3 = 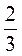 X + 5;
X + 5;
В) 21 – (4 – 6y) = y – 42;
Г) -5 – (3а + 1) – 11 = -16.
@ Звісно, що розв’язання рівнянь а) – в) учні виконують легко (на попередніх двох уроках подібні рівняння були розв’язані і спосіб розв’язання учням знайомий: а) переносимо доданки; б) спочатку помножимо обидві частини на 3, а потім переносимо доданки: в) спочатку ділимо обидві частини на 21, а потім переносимо доданки). Рівняння г) не вкладається в жодну з цих схем, тому або самі діти, або вчитель спрямовує думку учнів на те, що у випадку, коли в рівнянні застосовуємо розкриття дужок, рівняння коренів не змінить і тому:
-5 – (3a + 1) -11 = -16; 1)
-15a – 5 – 11 = -16; 2)
-15a – 16 = -16; 3)
-15a = 0; 4)
A = 0. 5)
Звернемо увагу на перехід від кроку 3) до кроку 4). Звісно, що учні запропонують перенести -16 з лівої частини у праву із протилежним знаком, тоді в правій частині будемо мати -16 + 16 = 0. Те ж саме будемо мати, якщо просто в рівнянні -15a – 16 = -16 прибираємо два рівних доданки в правій та лівій частинах: -15a – 16 = -16.
Після розв’язування всіх 4-х рівнянь підбиваємо підсумки, формулюємо своєрідний алгоритм розв’язування лінійних рівнянь з однією змінною:
1) Перевір, чи не треба помножити (поділити) обидві частини рівняння на одне й те саме число, що не дорівнює 0. Якщо так, виконай цю дію.
2) Перевір, чи не можна спростити вирази в лівій та правій частинах рівняння окремо (розкрити дужки, звести подібні доданки). Якщо так, спрости ці вирази.
3) Перевір, чи не знаходяться відомі та невідомі доданки в різних частинах рівняння. Якщо так, то перенеси доданки, щоб відомі числа знаходились в одній частині рівняння, а невідомі – в іншій.
4) Приведи рівняння до вигляду ах = b, де а і b – числа, а х – невідомий множник, і знайди цей невідомий множник.
(Бажано мати цей алгоритм у вигляді таблиці, яку кілька уроків поспіль будемо вивішувати біля дошки.) Хотілося, щоб учні усвідомили, що пропонований алгоритм є лише приблизною схемою дій і не завжди треба виконувати всі етапи під час розв’язування будь-якого рівняння. (Можливо, в деяких випадках п. 1) будемо виконувати, а в інших розпочнемо одразу з п. 3)).
VI. Вдосконалення вмінь
@ За допомогою алгоритму розв’язування рівнянь вдосконалюємо вміння учнів, вимагаючи свідомого вибору дій, що приведуть до розв’язування рівняння.
1. Розв’яжіть рівняння:
А) 4(х – 5) = 3х;
Б) 6(х + 2) = 18;
В) 2(2х + 4) = -3х;
Г) 2(х + 3) = 3(х – 4);
Д) -(3х + 1) = 2х;
Е) 3(2х – 5) = 5х + 3;
Ж) 2(у – 6) – 3y = 4y – y;
З) 2(x + 1,5) – 2 = x – 3;
К) 5,6х – 6 + 1,4x = 2,5(х – 1);
Л) -0,3(3 – х) = 0,3х + 0,3(5х + 2);
М) 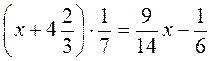 ;
;
Н) 3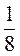 X – (3,5 – 2х) = 3
X – (3,5 – 2х) = 3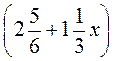 .
.
2. Додаткова логічна вправа. Знайдіть пропущене слово:
2х – 3 = 1 лютий
7х – 4 = 9х – 12 квітень
48 – 5х = 3 ?
VII. Підсумки уроку
Ігровий момент
Учитель. Учора, готуючись до уроку, я записав на окремих картках розв’язання одного рівняння, але потім картки переплутались. Чи не допоможете ви мені поновити правильний порядок карток?
Рівняння: -4 – (-z + 7) = z + 17.
Картки з розв’язанням:
1) 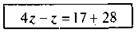 2)
2) 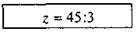 3)
3)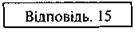
4) 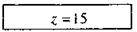 5)
5) 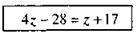 6)
6)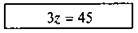
(Правильний порядок: 5), 1), 6), 2), 4) 3))
VIII. Домашнє завдання
1. Розв’яжіть рівняння, використовуючи алгоритм:
а) 5х – 4 = 3(х – 6);
Б) -(х – 4) = 2(х – 3);
В) 7(3х – 1) = -4х + 23;
Г) 3(3х – 1) + 5 = 8(х + 2) + 3;
Д) -5(у – 7) = 30 – (2у + 1);
Є) -4,5(х + 3) – 1 = 7,2 – 5(х – 2);
Ж) 3(2,4t – 3,5) + 6 = 9,7t – 3;
З) 5 – 4
– 4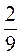 Х =
Х = 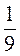 (х – 3).
(х – 3).
2. Виконайте дії 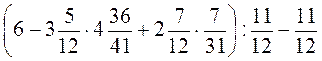 .
.