Головна ⇒ 📌Довідник з математики ⇒ Розв’язування найпростіших тригонометричних рівнянь
Розв’язування найпростіших тригонометричних рівнянь
Математика – Алгебра
Тригонометричні функції
Розв’язування найпростіших тригонометричних рівнянь
1. cos x = a
Розв’язки рівняння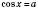 
шукатимемо, спираючись на рисунок 1 або на рисунок 2.
Якщо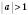 
, розв’язків немає.
, 
, 
.
, 
, 
.
, 
, 
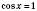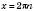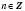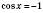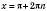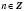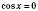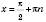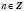
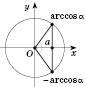
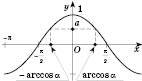
Рис. 2
Загальний випадок
: 
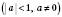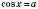, x = ±arccosa + 2πn,
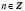.У випадках, коли
, 
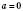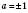, теж можна користуватися загальною формулою, але це не так раціонально.Розв’язки, які описуються загальною формулою, можна поділити на дві серії:
x1 = arccosa + 2πn, n Є Z;
x2 = – arccosa + 2πn, n Є Z.
2. sin x = a
Розв’язки шукатимемо, спираючись на рисунок 1 або на рисунок 2.
Якщо
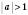, розв’язків
, 
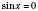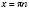, n Є Z.
, 
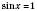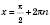, n Є Z.
, 
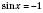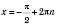, n Є Z.Загальний випадок
:
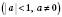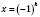
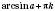, k Є Z.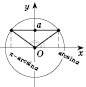
Рис. 1
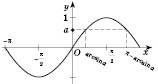
Рис. 2
Множина розв’язків розбивається на дві серії:
k = 2n, x1 = arcsina + 2πn, n Є Z;
k = 2n + 1, x2 = π – arcsina + 2πn, n Є Z.
3. tg x = a
Розв’язки запишемо, спираючись на рисунок зліва або на рисунок справа нижче.
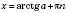, n Є Z.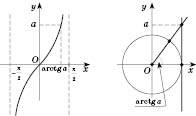
4. ctg x = a
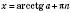, n Є Z.Якщо a = 0,
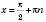, n Є Z.Якщо
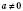, можна звести дане рівняння до рівняння 
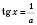.Приклади
1)
;
;
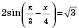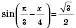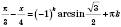, k Є Z;
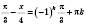, k Є Z;
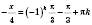, k Є Z;
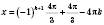, k Є Z.Множину розв’язків можна розбити на дві серії:
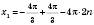, n Є Z;
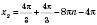, n Є Z;
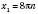, n Є Z;
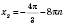, n Є Z.2)
;
;
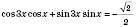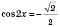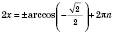, n Є Z;
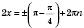, n Є Z;
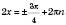, n Є Z;
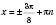, n Є Z.Related posts:
- Розв’язування найпростіших тригонометричних рівнянь. Рівняння sin t = a УРОК 21 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння sin t = а Мета уроку: засвоєння учнями виведення і застосування формули для коренів рівняння sin t = а. Обладнання: Таблиця “Рівняння sin t = а”. І. Перевірка домашнього завдання 1. Відповіді на питання, що виникли при виконанні домашніх завдань. 2. Самостійна робота. Варіант 1 Розв’яжіть рівняння: […]...
- Розв’язування найпростіших тригонометричних рівнянь. Рівняння cos t = a УРОК 20 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння cos T = a Мета уроку: засвоєння учнями виведення і застосування формули для знаходження коренів рівняння cos t = a. Обладнання: Таблиця “Рівняння cos t = a”. І. Перевірка домашнього завдання Математичний диктант Обчисліть: 1) arcsin ; 2) arcos ; 3) arctg ; 4) arcsin; 5) arccos; […]...
- Розв’язування найпростіших тригонометричних рівнянь. Рівняння tg t = a УРОК 22 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння tg T = a. Мета уроку: зсвоєння учнями виведення і застосування формули для знаходження коренів рівняння tg t = a (ctg t = а). Обладнання: Таблиця “Рівняння tg t = а і ctg t = a”. І. Перевірка домашнього завдання 1. Перевірити наявність домашніх завдань в зошитах […]...
- Деякі способи розв’язування тригонометричних рівнянь Математика – Алгебра Тригонометричні функції Деякі способи розв’язування тригонометричних рівнянь 1. Рівняння, що зводяться до квадратних . легко виразити через за допомогою основної тригонометричної тотожності : . Отже, ; . Нехай , . ; ; . 1) ; , k Є Z. 2) ; , k Є Z. Відповідь: , k Є Z; , k […]...
- Розв’язування найпростіших тригонометричних нерівностей Математика – Алгебра Тригонометричні функції Розв’язування найпростіших тригонометричних нерівностей Найзручнішим є спосіб розв’язування тригонометричних нерівностей за допомогою тригонометричного кола. Приклади 1) . Побудуємо одиничне коло (див. рисунок нижче). Проведемо пряму . Вона перетинає коло у двох точках. Одна з них відповідає куту або , друга – куту або . Ці дві точки розбивають коло на […]...
- Розв’язування однорідних тригонометричних рівнянь УРОК 25 Тема. Розв’язування однорідних тригонометричних рівнянь Мета уроку: формування умінь учнів розв’язувати однорідні тригонометричні рівняння. І. Перевірка домашнього завдання 1. Обговорення розв’язування вправи № 2 (6; 9; 11) за готовими розв’язаннями. 2. Розв’язування аналогічних вправ. А) 1 + cos x + cos 2x = 0; Б) cos4 x – sin4 x = ; В) […]...
- Розв’язування тригонометричних рівнянь способом зведення до однієї тригонометричної функції УРОК 23 Тема. Розв’язування тригонометричних рівнянь способом зведення до однієї тригонометричної функції Мета уроку: формування умінь учнів розв’язувати тригонометричні рівняння способом зведення до однієї тригонометричної функції (алгебраїчний спосіб). І. Перевірка домашнього завдання 1. Відповіді на питання, що виникли у учнів при виконанні домашніх завдань. 2. Самостійна робота. Розв’яжіть рівняння: A) cosx = . (3 бали) […]...
- Розв’язування тригонометричних рівнянь способом розкладання на множники УРОК 24 Тема. Розв’язування тригонометричних рівнянь способом розкладання на множники Мета уроку: фрмування умінь учнів розв’язувати тригонометричні рівняння способом розкладання на множники. І. Перевірка домашнього завдання Перший учень пояснює розв’язування вправи № 2 (23), другий учень – вправи № 2 (30), третій – вправи № 2 (37). II. Сприймання і усвідомлення нового матеріалу Багато тригонометричних […]...
- Розв’язування найпростіших тригонометричних нерівностей УРОК 29 Тема. Розв’язування найпростіших тригонометричних нерівностей Мета уроку: формування умінь учнів розв’язувати найпростіші тригонометричні нерівності: tg t > a, tgt < a, ctg t < a, ctg t > a (tgt a, tgt a, ctg t a, ctg t a). І. Перевірка домашнього завдання 1. Відповіді на запитання, які виникли в учнів у процесі […]...
- Розв’язування тригонометричних рівнянь, систем та нерівностей УРОК 31 Тема. Розв’язування тригонометричних рівнянь, систем та нерівностей Мета уроку. Систематизувати навички і уміння розв’язувати тригонометричні рівняння, нерівності, системи. І. Перевірка домашнього завдання 1. Три учні відтворюють розв’язування нерівностей із домашнього завдання. 2. Колективне розв’язування нерівностей: A) sin 2x sin x – cos 2x cos х . Sin 2x sin x – cos 2x […]...
- Розв’язування систем тригонометричних рівнянь УРОК 27 Тема. Розв’язування систем тригонометричних рівнянь Мета уроку: познайомити учнів з окремими прийомами розв’язування систем тригонометричних рівнянь. І. Перевірка домашнього завдання 1. Чотири учні відтворюють розв’язування домашніх завдань: вправа № 2 (10; 18; 26; 38). 2. Усне розв’язування тригонометричних рівнянь, використовуючи таблицю “Тригонометричні рівняння”. 1 2 3 4 1 Sin x = 0 Cos […]...
- Основні властивості рівнянь Математика – Алгебра Рівняння Два рівняння називають Рівносильними, якщо вони мають одні й ті ж корені; рівняння, які не мають коренів, також вважають рівносильними. Основні властивості рівнянь 1. Якщо виконати тотожні перетворення деякої частини рівняння, то одержимо рівняння, рівносильне даному. 2. Якщо деякий доданок перенести з однієї частини рівняння в іншу, змінивши при цьому його […]...
- Приклади розв’язування системи тригонометричних рівнянь Математика – Алгебра Тригонометричні функції Приклади розв’язування системи тригонометричних рівнянь 1) Відповідь: , n Є Z; , n Є Z. 2) а) б) Відповідь: , n, k Є Z; , n, k Є Z....
- Розв’язування рівнянь графічним способом Математика – Алгебра Функції Розв’язування рівнянь графічним способом За допомогою графіків функцій можна розв’язувати рівняння графічним способом. Для цього треба побудувати в одній системі координат графіки обох частин рівняння й знайти абсциси точок їх перетину. Приклад. Розв’яжіть рівняння . Побудуємо графіки функції і в одній координатної системі (див. рисунок) і знайдемо абсиси точок їх перетину. […]...
- Графік лінійного рівняння з двома невідомими – Системи лінійних рівнянь Математика – Алгебра Системи лінійних рівнянь Графік лінійного рівняння з двома невідомими Графіком рівняння з двома невідомими називається множина всіх точок координатної площини, координати котрих є розв’язками цього рівняння. Графіком рівняння , у якому хоча б один із коефіцієнтів (a або b) відмінний від нуля, є пряма. Для побудови будь-якої прямої досить знати координати двох […]...
- Системи рівнянь – РІВНЯННЯ Формули й таблиці МАТЕМАТИКА РІВНЯННЯ Лінійне рівняння з однією змінною – рівняння, що зводиться до канонічного вигляду ах + b = 0, де х – змінна, а й b – константи. Корінь рівняння ах + b = 0 визначається формулою: х = – b/а – якщо а ≠ 0, множина розв’язків L = {-b/a}. – […]...
- Системи лінійних рівнянь з двома невідомими – Системи лінійних рівнянь Математика – Алгебра Системи лінійних рівнянь Системи лінійних рівнянь з двома невідомими Якщо треба знайти спільні розв’язки кількох рівнянь, то кажуть, що ці рівняння утворюють Систему рівнянь. Розв’язок системи рівнянь з двома невідомими – пара значень невідомих, яка є розв’язком кожного з рівнянь системи. Розв’язати систему рівнянь означає знайти всі її розв’язки або довести, що […]...
- Види неповних квадратних рівнянь і їх розв’язання Математика – Алгебра Квадратні корені Види неповних квадратних рівнянь і їх розв’язання 1. Якщо , , квадратне рівняння набуває вигляду і має один корінь . 2. Якщо , , квадратне рівняння набуває вигляду . Розв’язуючи його, маємо: ; або . Рівняння має два корені: і . 3. Якщо , , квадратне рівняння набуває вигляду . […]...
- Розв’язування систем рівнянь Математика – Алгебра Розв’язування систем рівнянь Розглянемо системи рівнянь, в яких одне або обидва рівняння другого степеня. 1. Щоб розв’язати систему рівнянь графічним способом, треба побудувати в одній системі координат графіки обох рівнянь системи й знайти координати точок перетину графіків. Ці точки і будуть розв’язками системи рівнянь. Наприклад: Графіком першого рівняння є коло з центром […]...
- Розв’язування рівнянь та задач за допомогою рівнянь Урок № 105 Тема. Розв’язування рівнянь та задач За допомогою рівнянь Мета: підгодовувати учнів до виконання тематичної контрольної роботи. Тип уроку: узагальнення та систематизації знань. Хід уроку I. Організаційний момент II. Перевірка домашнього завдання На окремих аркушах учні в завданнях 1 та 2 записують рівняння та його розв’язок; у завданні № 3 відповідь; після того […]...
- Графіки тригонометричних функцій Математика – Алгебра Тригонометричні функції Графіки тригонометричних функцій Для побудування графіків тригонометричних функцій візьмемо . Побудуємо графік функції (див. рисунок). Ця крива називається синусоїдою. Графік функції можна дістати з графіка функції паралельним перенесенням його вліво вздовж осі Ox на одиниць. Це випливає з формули . Побудуємо графік функції : Зверніть увагу: значення , , не […]...
- Рівняння з двома змінними – Системи лінійних рівнянь Математика – Алгебра Системи лінійних рівнянь Рівняння з двома змінними Лінійним рівнянням з двома невідомими Називається рівняння виду , де x і y – невідомі, a, b, і с – числа (Коефіцієнти рівняння). Розв’язком рівняння з двома невідомими називається пара значень невідомих, при яких рівняння перетворюється у правильну числову рівність. Наприклад: ; – розв’язок рівняння, […]...
- Розв’язування показникових рівнянь і систем показникових рівнянь УРОК 48 Тема. Розв’язування показникових рівнянь і систем показникових рівнянь Мета уроку. Формування уміння розв’язувати показникові рівняння і системи показникових рівнянь. І. Перевірка домашнього завдання 1. Чотири учні відтворюють розв’язування вправи № 1 (25, 28, 30, 46). 2. Усне розв’язування показникових рівнянь за допомогою таблиці 20 для усних обчислень “Показникові рівняння” 1 2 3 4 […]...
- Системи рівнянь з двома змінними. Графічний спосіб розв’язування систем рівнянь з двома змінними УРОК № 30 Тема. Системи рівнянь з двома змінними. Графічний спосіб розв’язування систем рівнянь з двома змінними Мета уроку: закріпити знання учнів про зміст означень: графік рівняння з двома змінними, система рівнянь з двома змінними, розв’язок системи рівнянь з двома змінними, а також алгоритмів побудови графіка рівняння з двома змінними та графічного способу розв’язування системи […]...
- Поняття рівняння. Розв’язування рівнянь 770. а) 5х = 3х + 4. Х = 2 – корінь рівняння, бo 5 • 2 = 3 • 2 + 4 – правильна рівність. Б) 2х + 8 = 7х. Х = 2 – не є коренем рівняння, 2 • 2 + 8 = 7 • 2 – неправильна рівність. В) 10 – […]...
- Лінійне рівняння з однією змінною. Розв’язування лінійних рівнянь з однією змінною і рівнянь, що зводяться до них Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 23. Лінійне рівняння з однією змінною. Розв’язування лінійних рівнянь з однією змінною і рівнянь, що зводяться до них Ми знаємо, як розв’язувати рівняння 2х = -8; х – 5; 0,01х -17. Кожне із цих рівнянь має вигляд ах = b, де х – змінна, а і b […]...
- Підсумковий урок з теми “Квадратний тричлен. Розв’язування рівнянь, що зводяться до квадратних рівнянь та їх використання для розв’язування текстових задач” Урок № 63 Тема. Підсумковий урок з теми “Квадратний тричлен. Розв’язування рівнянь, що зводяться до квадратних рівнянь та їх використання для розв’язування текстових задач” Мета: повторити, систематизувати та узагальнити знання і вміння учнів щодо можливості та способів застосування розв’язання квадратного рівняння для розкладання квадратного тричлена на лінійні множники, розв’язування біквадратних та дробово-раціональних рівнянь, а також […]...
- Розв’язування рівнянь Математика – Алгебра Раціональні числа Розв’язування рівнянь Властивості рівнянь Корені рівнянь не змінюються, якщо до обох частин додати будь-який доданок. Отже, при розв’язуванні рівнянь доданки можна переносити з однієї частини в другу, змінюючи при цьому їхні знаки на протилежні. Корені рівнянь не змінюються, якщо обидві його частини помножити або поділити на одне й те ж […]...
- Складання найпростіших окисно-відновних реакцій, підбір коефіцієнтів Тема 2 ХІМІЧНІ РЕАКЦІЇ Урок 28 Тема уроку. Складання найпростіших окисно-відновних реакцій, підбір коефіцієнтів Цілі уроку: розвивати навички складання окисно-відновних реакцій; закріпити навички складання хімічних рівнянь на прикладі найпростіших окисно-відновних реакцій, застосування методу електронного балансу для розміщення коефіцієнтів у рівняннях хімічних реакцій, що протікають зі зміною ступеня окиснення. Тип уроку: узагальнення й систематизації знань, умінь […]...
- Розв’язування систем двох лінійних рівнянь з двома змінними способом підстановки Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 28. Розв’язування систем двох лінійних рівнянь з двома змінними способом підстановки Графічний спосіб розв’язування систем рівнянь є досить громіздким і до того ж не завжди допомагає знайти точні розв’язки. Розглянемо інші (не графічні) способи розв’язування систем лінійних рівнянь з двома змінними, які називають аналітичними. Почнемо зі способу […]...