Розв’язування вправ. Самостійна робота
УРОК 4
Тема. Розв’язування вправ. Самостійна робота
Мета уроку: формування умінь будувати графіки функцій за допомогою геометричних перетворень.
І. Перевірка домашнього завдання
1. Один учень відтворює розв’язування вправи № 3 (4; 5; 6), другий – № 3 (7; 8; 9), третій – № 3 (18).
2. Математичний диктант.
Запишіть формулою функцію, графік якої одержано в результаті:
1) паралельного перенесення графіка функції у = 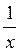 на 3 одиниці вздовж осі ОХ.
на 3 одиниці вздовж осі ОХ.
2) паралельного перенесення графіка функції у =
3) паралельного перенесення графіка функції у = х3 на 3 одиниці вздовж осі??.
4) паралельного перенесення графіка функції у = х2 на -3 одиниці вздовж осі ОУ.
5) розтягу графіка функції у = |х| від точки (0; 0) вздовж осі ординат у 3 рази.
6) стиску графіка функції 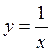 до точки (0; 0) вздовж осі абсцис у 3 рази.
до точки (0; 0) вздовж осі абсцис у 3 рази.
Відповідь: 1) 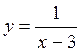 ; 2)
; 2) 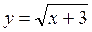 ; 3) у = х3 + 3 ; 4) у = х3 – 3; 5) у = 3 |х|; 6)
; 3) у = х3 + 3 ; 4) у = х3 – 3; 5) у = 3 |х|; 6) 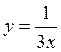 .
.
II. Формування умінь учнів будувати графіки функцій за допомогою геометричних перетворень
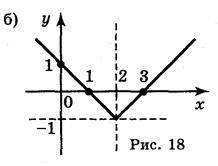
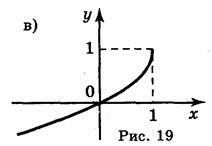
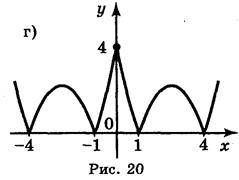
1. Побудуйте графіки функцій:
А)
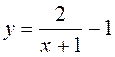 ; б) у = |х – 2| – 1; в)
; б) у = |х – 2| – 1; в) 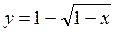 ; г) у= x2 – 5|x| + 4.
; г) у= x2 – 5|x| + 4.Відповідь:
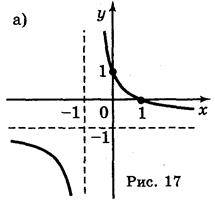
III. Самостійна робота
1. Знайдіть область визначення функції: 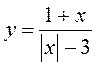 (3 бали)
(3 бали)
2. Дослідіть на парність і непарність функцію у = х3 – х (3 бали)
3. Побудуйте графік функції:
А) 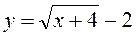 (3 бали)
(3 бали)
Б) у = |х|3 – 1 (3 бали)
Відповідь: 1) D(y) = (- ;-3)
;-3)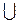 (-3;3)
(-3;3)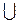 (3;+
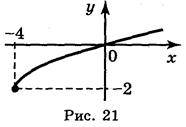
(3;+ ); 2) непарна; 3) а) рис. 21; б) рис. 22.
); 2) непарна; 3) а) рис. 21; б) рис. 22.
1. Знайдіть область визначення функції: 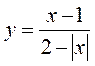 (3 бали)
(3 бали)
2. Дослідіть на парність і непарність функцію у = х4 – х2. (З бали)
3. Побудуйте графік функції:
А) 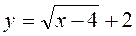 (3 бали) б) у = |х3 – 1| (3 бали)
(3 бали) б) у = |х3 – 1| (3 бали)
Відповідь:1) D(y)=(- ;-2)
;-2)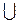 (-2;2)
(-2;2)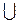 (2;+
(2;+ ) 2) парна.
) 2) парна.
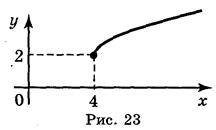
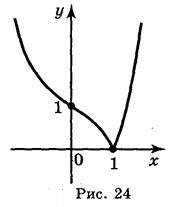
2) а) рис. 23; б) рис. 24.
IV. Підсумок уроку
V. Домашнє завдання
Розділ І § 1 (3). Вправа № 3 (20; 32; 28).
Related posts:
- Застосування властивостей показникової функції до розв’язування вправ УРОК 44 Тема. Застосування властивостей показникової функції до розв’язування вправ Мета уроку. Формування умінь учнів застосовувати властивості показникової функції до розв’язування вправ. Познайомити учнів з використанням показникової функції під час вивчення явищ навколишнього середовища. І. Перевірка домашнього завдання Колективне обговорення № 1-12 із “Запитання і завдання для повторення” § 1 розділу IV. II. Набуття умінь […]...
- Повторення та систематизація знань та вмінь учнів з теми “Функції і графіки” Урок № 85 Тема. Повторення та систематизація знань та вмінь учнів з теми “Функції і графіки” Мета: повторити та систематизувати набуті учнями знання про зміст основних понять теми та види задач; повторити та систематизувати основні способи дій, що були опановані учнями під час вивчення теми; провести підготовку до підсумкового тематичного оцінювання. Тип уроку: повторення та […]...
- Розв’язування задач і вправ. Самостійна робота № 6 Урок № 52 Тема. Розв’язування задач і вправ. Самостійна робота № 6 Мета. Формувати в учнів навички і вміння розв’язувати задачі геометричного змісту, удосконалювати вміння працювати в груп, виховувати почуття відповідальності за доручену справу, розвивати логічне мислення, шляхом розв’язування задач. Обладнання: підручник стор 152-153. Тип уроку: урок перевірки знань, навичок і вмінь. Хід уроку I. […]...
- РОЗВ’ЯЗУВАННЯ ЗАДАЧ. Самостійна робота № 7 Тип уроку: урок формування навичок розв’язування задач. Поточний контроль знань. Мета: формувати вміння розв’язувати задачі: аналізувати умову, грамотно оформлювати задачі, робити необхідні креслення; здійснити поточний контроль знань учнів з метою корекції. Обладнання та наочність: картки або збірники із задачами. Відеофрагмент:________________________________ Хід уроку I. ОРГАНІЗАЦІЙНИЙ ЕТАП II. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ III. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ ТА ВМІНЬ […]...
- Найпростіші перетворення графіків функцій УРОК № 21 Тема. Найпростіші перетворення графіків функцій Мета уроку: закріпити знання учнів про види геометричних перетворень графіків функцій і зв’язок між видом перетворення та видом рівняння, що задає дану функцію. Закріпити схеми міркувань, що передують побудові графіка деякої функції шляхом геометричних перетворень графіка однієї з елементарних функцій. Закріпити вміння виконувати послідовні перетворення графіків елементарних […]...
- Графіки тригонометричних функцій Математика – Алгебра Тригонометричні функції Графіки тригонометричних функцій Для побудування графіків тригонометричних функцій візьмемо . Побудуємо графік функції (див. рисунок). Ця крива називається синусоїдою. Графік функції можна дістати з графіка функції паралельним перенесенням його вліво вздовж осі Ox на одиниць. Це випливає з формули . Побудуємо графік функції : Зверніть увагу: значення , , не […]...
- Побудова графіків тригонометричних функцій УРОК 9 Тема. Побудова графіків тригонометричних функцій Мета уроку: побудова графіків функцій у = sin х, у = cos x, у = tg х, у = ctg x. Формування умінь будувати графіки функцій: у = Asin (kx + b), у = Acos (kx + b), у = Atg (kx + b), у = Actg (kx […]...
- Функції Урок № 68 Тема. Функції Мета: виявити рівень засвоєння обов’язкових знань та вмінь з теми “Функція”, передбачених програмою з математики та ступінь сформованості навичок. Тип уроку: контроль знань та вмінь. Форма проведення: тематична контрольна робота. Хід уроку І. Перевірка домашнього завдання II. Умова тематичної контрольної роботи Варіант 1 Варіант 2 1?. Функцію задано формулою У […]...
- Обернені тригонометричні функції: у = arcsin х, у = arccos х УРОК 18 Тема. Обернені тригонометричні функції: у = arcsin х, у = arccos х Мета уроку: вивчення властивостей обернених тригонометричних функцій: у = arcsin х, у = arccos х. І. Перевірка домашнього завдання Математичний диктант. Закінчіть математичні твердження: 1. Функція, яка набуває кожного свого значення в єдиній точці області визначення називається… 2. Оберненою до функцій […]...
- Контрольна робота № 7 (підсумкова) УРОКИ 63-70 Уроки 63-70 відповідають V розділу програми з алгебри та початків аналізу “Резерв навчального часу”, і вчитель може використовувати цей час на власний розсуд з урахуванням рівня математичної підготовки учнів. Ці години можна використати на повторення на початку навчального року, як додаткові години на окремі теми або для узагальнення й систематизацію матеріалу і повторення […]...
- Розв’язування вправ. Самостійна робота № 9 Тема. Розв’язування вправ. Самостійна робота № 9 Мета уроку. Узагальнення і систематизація учнів з теми “Ділення натуральних чисел.” Хід уроку І. Організація класу ІІ. Перевірка домашнього завдання Перевірити наявність виконання домашніх завдань. ІІІ. Виконання вправ Колективно № 1425, № 1427, № 1428 (а, б) – колективно, (в, г) – самостійно. Колективно № 1430. ІV. Самостійна […]...
- Функції та їхні властивості. Квадратична функція УРОК № 62 Тема. Функції та їхні властивості. Квадратична функція Тестові завдання 1. Знайдіть область визначення функції . А) х 5; Б) х -5; В) х -5, х 0; Г) х 3, х -5, х 0. 2. Знайдіть нулі функції . А) 0; 2; б) 2; в) 0; -2; г) нулів немає. 3. Яка з […]...
- Розв’язування задач і вправ. Самостійна робота № 7 Урок № 7 Тема. Розв’язування задач і вправ. Самостійна робота № 7 Мета уроку. Формування навичок розв’язування задач на звичайні дроби, перевірити ступінь засвоєння вивченого. Хід уроку I. Перевірка домашнього завдання Учні коментують розв’язки виконаних вправ. II. Самостійна робота №9 Варіант І 1. При яких значеннях n дріб правильний? 2. Порівняй числа : а ) […]...
- Розв’язування задач і вправ. Самостійна робота № 2 Урок № 20. Тема. Розв’язування задач і вправ. Самостійна робота № 2 Мета. Поглиблювати уміння та навички учнів користуватися поняттями відрізка, ламаної, прямої координатного променя та шкал, а також вимірювати величину кутів. Розвивати кмітливість, інтерес до геометрії, виховувати почуття відповідальності. Хід уроку I. Організація класу II. Перевірка домашнього завдання 1. Два учні працюють біля дошки. […]...
- Розв’язування задач і вправ. Самостійна робота № 5 Урок № 45 Тема. Розв’язування задач і вправ. Самостійна робота № 5 Мета уроку. Перевірити в учнів навики розв’язування рівнянь, задач на складання рівнянь в знайомих і змінених ситуаціях. Розвивати самостійні навики у роботі, здібності – на основі розумових дій і операцій. Виховувати вміння раціонально використовувати робочий час. Обладнання. Підручник. Хід уроку І. Повідомлення теми […]...
- Розв’язування задач і вправ. Самостійна робота № 8 Урок № 31 Тема. Розв’язування задач і вправ. Самостійна робота № 8 Мета. Продовжувати формувати навички розв’язування задач і вправ на використання правил множення десяткових дробів. Хід уроку І. Актуалізація опорних знань. 1) Правило множення десяткових дробів. 2) Множення десяткового дробу на 10, 100 і т. д. 3) Множення десяткового дробу на 0,1, 0,001 і […]...
- Огляд властивостей основних функцій УРОК 2 Тема. Огляд властивостей основних функцій Мета уроку: Повторення і узагальнення властивостей елементарних функцій: у = kx + b, у = , у = х2, у= х3, у = , у = , у = ?х2 + bx + с. І. Перевірка домашнього завдання 1. Один учень пояснює розв’язання вправи № 1 (5), другий […]...
- Розв’язування задач і вправ. Самостійна робота № 1- МАТЕМАТИКА Мета: Навчити учнів розв’язувати задачі і вправи з теми “Натуральні числа ” Вчити учнів самостійно працювати. Учні повинні вміти: записувати натуральні числа словами і цифрами, порівнювати їх, розв’язувати задачі і вправи з натуральними числами. І. Перевірка домашнього завдання Клас поділено на дві команди Командам дається однакова кількість запитань. Хто більше набере балів. Та команда виграє. […]...
- РОЗВ’ЯЗУВАННЯ ВПРАВ І ЗАДАЧ НА ЗАСВОЄННЯ ТАБЛИЦІ ДІЛЕННЯ НА 5. ЗНАХОДЖЕННЯ ЗНАЧЕНЬ БУКВЕНИХ ВИРАЗІВ. САМОСТІЙНА РОБОТА Мета: формувати навички розв’язування прикладів і задач, які включають дії різних ступенів; розвивати логічне мислення; виховувати самостійність, інтерес до вивчення математики. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Перевірка домашнього завдання (с. 123, завдання 751; 752.) Завдання 751 – Прочитайте складені вирази та їх значення. Завдання 752 – Скільки вийшло рядів? 2. […]...
- Розв’язування ірраціональних нерівностей УРОК 39 Тема. Розв’язування ірраціональних нерівностей Мета уроку. Познайомити учнів з узагальненим методом інтервалів. Формування умінь розв’язувати ірраціональні нерівності. І. Перевірка домашнього завдання 1. Перевірити розв’язування вправ № 71 (3), 67 (1), 79 (1) за розв’язаннями на дошці, заготовленими до уроку. 2. Самостійна робота Розв’яжіть рівняння: А) = . (4 бали) Б) – = 2. […]...
- Графік функції Урок № 63 Тема. Графік функції Мета: формувати вміння виконувати побудову графіка функції, заданої формулою “по точках”; відпрацьовувати навички “читання” графіків функцій; провести діагностику засвоєння матеріалу з теми “Функція. Графік функції”. Хід уроку I. Організаційний момент Вступне слово вчителя. Перевірка готовності учнів до уроку; місце уроку в темі, план роботи на уроці. II. Перевірка домашнього […]...
- Перетворення графіків функцій – Функції та графіки Математика – Алгебра Функції та графіки Перетворення графіків функцій 1. Графіки функцій і є симетричними відносно осі Ox. 2. Щоб побудувати графік функції , треба графік функції розтягнути від осі Ox в k разів, якщо , або стиснути його в k разів до осі Ox, якщо . 3. Щоб побудувати графік функції , треба графік […]...
- Завдання для перевірки знань до §§ 19-21 1. 1) у = х2 + х; 3) – функції. 2. 1) у = 3х – 7; 3) у = 4 – лінійні функції. 3. 1) у = -2х + 6; k = -2; l = 6; 2) у = 7,4x; k = 7,4; l = 0. 4. у = -2х + 7; 1) х […]...
- Приклади функцій і їх графіків Математика – Алгебра Функції Приклади функцій і їх графіків Лінійна функція Лінійною називається функція, яку можна задати формулою , де х – аргумент, а k і b – дані числа. Графік лінійної функції – пряма. k називається Кутовим коефіцієнтом прямої, яка є графіком лінійної функції. Кожна пряма на координатній площині, яка не є перпендикулярною до […]...
- Побудова графіків функцій за допомогою геометричних перетворень відомих графіків функцій УРОК 3 Тема. Побудова графіків функцій за допомогою геометричних перетворень відомих графіків функцій Мета уроку: Формування умінь будувати графіки функцій за допомогою восьми базових перетворень графіка функції У = f(x): у = – f(x); у = f(-x); у = f(x) + b; у = f(x + a); у = af(x); у = f(ax); у = […]...
- Розділ 4. Функції Або немає розв’язку. 6. 1) Так; 2) ні; 3) ні; 4) так. 7. 1) -4 = -2 • (-1)2 – 3 + 1; -4 = -2 – 3 + 1; -4 = -4; А належить графіку функції; 2) 0 ≠ -2 • 12 + 3 + 1; 0 ≠ -2 + 4; 0 ≠ 2; […]...
- Лінійна функція, її графік та властивості Урок № 65 Тема. Лінійна функція, її графік та властивості Мета: ознайомити учнів із “особливими випадками” лінійної функції і її графіком; узагальнити уяву учнів про зв’язок між k та b і графіком; подальше вдосконалювати вміння будувати й читати графіки лінійних функцій. Тип уроку: засвоєння вмінь та навичок. Хід уроку I. Організаційний момент (див. попередній урок) […]...
- Показникова функція, її графік і властивості УРОК 43 Тема. Показникова функція, її графік і властивості Мета уроку. Засвоєння учнями поняття показникової функції, її властивостей і графіка. Обладнання. Таблиця “Показникова функція”. І. Аналіз контрольної роботи II. Повідомлення теми уроку III. Сприймання і усвідомлення нового матеріалу Функція виду у = ах, де а > 0, а? 1, називається показниковою (з основою а). Усне […]...
- Функції та графіки. Лінійна функція Урок № 67 Тема. Функції та графіки. Лінійна функція Мета: повторити та узагальнити відомості щодо змісту основних понять теми; повторити, систематизувати набуті практичні вміння; провести підготовку до тематичної контрольної роботи. Тип уроку: узагальнення та систематизація знань, умінь, навичок. Хід уроку I. Організаційний момент 1. Готовність до уроку. 2. План роботи на уроці. II. Перевірка домашнього […]...
- ПОВТОРЕННЯ. ФУНКЦІЇ Цілі: – навчальна: узагальнити та систематизувати знання учнів про зміст основних понять теми “Функції”; – розвивальна: формувати вміння аналізувати й узагальнювати інформацію, бачити закономірності; розвивати увагу, логічне мислення, пам’ять; – виховна: виховувати відповідальність за результати своєї роботи, наполегливість у досягненні мети, віру у власні сили; Тип уроку : узагальнення та систематизація знань. Обладнання та наочність: […]...