Система двох лінійних рівнянь з двома змінними та її розв’язок. Розв’язування систем лінійних рівнянь з двома змінними графічно
Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ
& 27. Система двох лінійних рівнянь з двома змінними та її розв’язок. Розв’язування систем лінійних рівнянь з двома змінними графічно
Приклад 1. Маска й трубка для підводного плавання разом коштують 96 грн, причому маска на 16 грн дорожча за трубку. Скільки коштує маска і скільки трубка?
Р о з в ‘ я з а н н я. Цю задачу можна розв’язати арифметичним способом (по діях) або за допомогою рівняння з однією
Змінною. А ще її можна розв’язати за допомогою лінійних рівнянь з двома змінними.
Нехай
Оскільки маска дорожча за трубку на 16 грн, то маємо ще одне рівняння: х – у = 16.
Одержали два рівняння з двома змінними, які є математичною моделлю задачі. Щоб розв’язати задачу, треба знайти такі значення змінних х і у, які б одночасно перетворювали у правильну рівність кожне з одержаних рівнянь, тобто знайти спільний розв’язок цих рівнянь.
Якщо є кілька рівнянь, для яких треба знайти спільний розв’язок рівнянь, то кажуть, що ці рівняння утворюють систему рівнянь. Записують систему
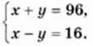
Пара значень змінних х = 56, у = 40 є розв’язком кожного з рівнянь системи. Таку пару чисел називають розв’язком системи.
Для розв’язування системи лінійних рівнянь з двома змінними, можна використовувати графіки рівнянь. Такий спосіб розв’язування систем рівнянь називають графічним.
Приклад 2. Розв’язати систему рівнянь:
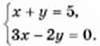
Р о з в ‘ я з а н н я. Побудуємо в одній координатній площині графіки обох рівнянь (мал. 37). Координати кожної точки прямої, яка є графіком рівняння х + у = 5, задовольняють це рівняння. Аналогічно, координати кожної точки прямої 3х – 2у = 0 задовольняють це рівняння. Координати точки перетину прямих задовольняють як перше, так і друге рівняння, тобто є розв’язком кожного з рівнянь, отже, і розв’язком даної системи рівнянь. Оскільки графіки перетинаються лише в точці (2; 3), то система має єдиний розв’язок х = 2; у = 3. Перевіркою (підстановкою в кожне з рівнянь системи) пересвідчуємося, що знайдена пара чисел дійсно є розв’язком даної системи. Цей розв’язок можна записати ще так: (2; 3), де на першому місці значення змінної х, а на другому – значення змінної у.
В і д п о в і д ь: (2; 3).
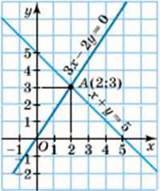
Мал. 37
Зауважимо, що графічний спосіб зазвичай дає змогу знаходити розв’язки лише наближено. Але, підставивши значення х =2 і у = 3 в кожне з рівнянь даної системи, переконуємося, що ця пара чисел є їх розв’язком, отже, пара (2; 3) виявилася точним розв’язком.
Розглянемо системи двох лінійних рівнянь з двома змінними, у кожному з яких хоча б один з коефіцієнтів при змінних х і у відмінний від нуля. Графіками обох рівнянь системи є прямі. Якщо ці прямі перетинаються, то система має єдиний розв’язок; якщо прямі не перетинаються (паралельні), то система не має розв’язків; якщо прямі збігаються, то система має безліч розв’язків.
Отже, щоб розв’язати систему рівнянь графічно, доцільно дотримуватися такої послідовності дій:
1) побудувати графіки рівнянь системи в одній координатній площині;
2) знайти координати точки перетину графіків або впевнитися, що графіки рівнянь не перетинаються (є паралельними) або збігаються;
3) якщо координати точки перетину є цілими числами, то виконати перевірку: якщо ні, то розв’язок системи визначити наближено;
4) записати розв’язок у відповідь.
Приклад 3. Розв’язати систему рівнянь:
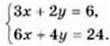
Р о з в ‘ я з а н н я. 1-й спосіб. Побудуємо графіки рівнянь в одній координатній площині (мал. 38). Графіки рівнянь є паралельними прямими, тому система розв’язків не має.
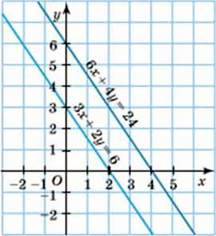
Мал. 38
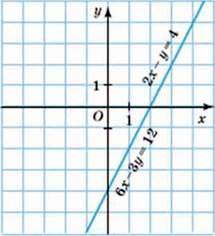
Мал. 39
2-й спосіб. Поділивши обидві частини другого рівняння на 2, матимемо:
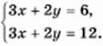
Очевидно, що не існує таких значень змінних х і у, для яких би одночасно виконувалися рівності 3х + 2у – 6 і 3х + 2у = 12. Отже, система рівнянь розв’язків не має.
В і д п о в і д ь: не має розв’язків.
Приклад 4. Розв’язати систему рівнянь:
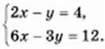
Р о з в ‘ я з а н н я. 1-й спосіб. Побудуємо графіки рівнянь в одній координатній площині (мал. 39). Графіки рівнянь збігаються, тому дана система має безліч розв’язків. Будь-яка пара чисел, яка задовольняє перше рівняння, задовольняє також і друге. Щоб записати відповідь до системи, виразимо у через х з першого рівняння: у = 2х – 4. Таким чином, будь-яка пара чисел вигляду (х; 2х – 4), де х – довільне число, є розв’язком даної системи.
2-й спосіб. Поділивши обидві частини другого рівняння на 3, матимемо:
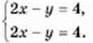
Очевидно, що маємо два однакових рівняння, отже, і графіки їх збігаються. Потім міркуємо так само, як у 1-му способі.
В і д п о в і д ь: (х; 2х – 4), де х – довільне число.
А ще раніше…
Китайські математики вміли розв’язувати системи лінійних рівнянь 2000 років тому.
Вони винайшли загальний метод розв’язування таких систем, причому не тільки з двома, а й з більшою кількістю рівнянь і змінних.
А давньогрецький математик Діофант (бл. IІІ ст. до н е.) розв’язував і деякі системи нелінійних рівнянь з двома змінними.
Що називають розв’язком системи рівнянь з двома змінними? Що означає розв’язати систему рівнянь? Скільки розв’язків може мати система двох лінійних рівнянь з двома змінними? Як розв’язати систему двох лінійних рівнянь з двома змінними графічно?
1001. (Усно) Яка з даних систем є системою двох лінійних рівнянь з двома змінними:
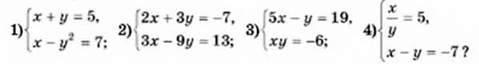
1002. (Усно) Чи є розв’язком системи рівнянь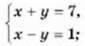 
пара чисел:
1) (3; 4);
2) (4; 3);
3) (6; 1)?
1003. Яка з даних пар чисел є розв’язком системи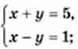 
1) (5; 0);
2) (2; 3);
3) (3; 2)?
1004. (Усно) Скільки розв’язків має система, графіки рівнянь якої зображено на малюнку 40? На малюнку 41?
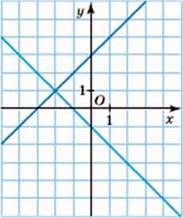
Мал. 40
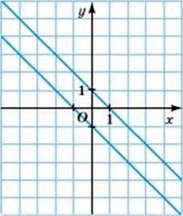
Мал. 41
1005. (Усно) Чи є пара чисел (-2; 1) розв’язком системи:
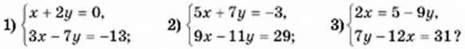
1006. Яка з пар (3; -4), (7; 2), (4; -3) є розв’язком системи:
1007. Складіть систему лілійних рівнянь з двома змінними, розв’язком якої є пара чисел:
1) (1; -3);
2) (4; 5).
1008. Знайдіть координати точки перетину прямих, зображених на малюнку 42. Запишіть відповідну систему рівнянь. Перевірте розв’язок, підставивши координати знайденої точки в кожне з рівнянь.
1009. Розв’яжіть систему рівнянь графічно:
1010. Розв’яжіть систему рівнянь графічно:
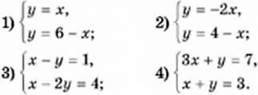
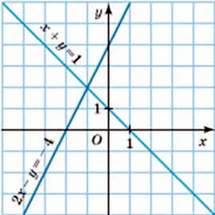
Мал. 42
1011. Пара (2; -5) є розв’язком системи рівнянь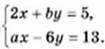 
Знайдіть а і b.
1012. Знайдіть а і b, якщо пара (10; -2) є розв’язком системи рівнянь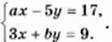 
1013. Розв’яжіть систему рівнянь графічно:
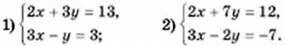
1014. Розв’яжіть систему рівнянь графічно:
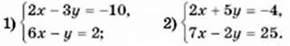
1015. З’ясуйте, чи має система розв’язки і скільки:
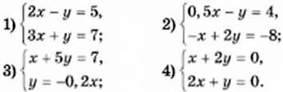
1016. Чи має система розв’язки і скільки:
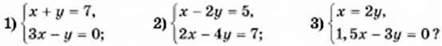
1017. Розв’яжіть графічно систему рівнянь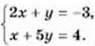 
Перевірте, чи є одержаний розв’язок точним. Чи є розв’язком даної системи пара чисел (- 2 
; 1 
)?
1018. Розв’яжіть графічно систему рівнянь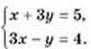 
Перевірте, чи є одержаний розв’язок точним. Чи є розв’язком даної системи пара чисел (1,9; 1,7)?
1019. Не виконуючи побудови, доведіть, що система рівнянь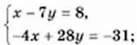 
не має розв’язків.
1020. Не виконуючи побудови, доведіть, що система рівнянь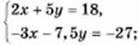 
має безліч розв’язків.
1021. Знайдіть які-небудь розв’язки системи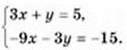 
Скільки всього розв’язків вона має? Розв’яжіть її.
1022. Розв’яжіть систему рівнянь:
1023. До рівняння х + 3у = 5 доберіть друге рівняння так, щоб одержана система рівнянь мала:
1) лише один розв’язок;
2) безліч розв’язків.
1024. До рівняння 2х – у = 7 доберіть друге рівняння так, щоб одержана система рівнянь не мала розв’язків.
Вправи для повторення
1025. Які з точок А(4; -2); В(0; 0); С(-1; 5); D(1; 2) належать графіку прямої пропорційності:
1 )у = – 
Х;
2) у = 5х?
1026. Спростіть вираз:
1) 7m(m – 3) – 3(m – 2)(m + 2);
2) (1 – 2х)(2х + 1) – (3х – 1)2;
3) (2х + 3у)2 – (х + 3y)(2х – у);
4) (4а – 5b)(5b + 4а) – (2а – 5b)2.
1027. Доведіть, що вираз х2 + 8х – 17 при будь-яких значеннях х набуває лише від’ємних значень. Якого найбільшого значення набуває цей вираз і при якому значенні х?
Цікаві задачі для учнів неледачих
1028. Припустимо, що вираз (4 – 3х)2015 подано у вигляді многочлена. Знайдіть суму коефіцієнтів цього многочлена.
Цікаві задачі для учнів неледачих
1000. Доведіть, що для будь-якого значення х значення виразу х8- х5 +х2- x + 1 є числом додатним.
(1 votes, average: 5.00 out of 5)
Loading...