Системи двох лінійних рівнянь із двома змінними та графічний спосіб розв’язування систем
Урок № 73
Тема. Системи двох лінійних рівнянь із двома змінними та графічний спосіб розв’язування систем
Мета: засвоїти знання щодо залежності кількості розв’язків системи лінійних рівнянь від співвідношення коефіцієнтів a, b, c цих рівнянь; вироблення вмінь застосовувати названу ознаку під час графічного розв’язання систем рівнянь; подальше вдосконалювати вміння розв’язувати системи лінійних рівнянь графічним способом.
Тип уроку: засвоєння нових знань.
Хід уроку
I. Організаційний момент
1. Перевірка готовності
2. План роботи (місце уроку в темі).
II. Перевірка домашнього завдання
@ Перевірити на уроці бажано не тільки розв’язання письмових вправ, але й теоретичну частину. Тому на початку уроку пропонуємо учням контрольні запитання (див. попередній урок), а потім проводимо інтерактивну вправу “Мікрофон”. Після перевірки теоретичних знань, організуємо перевірку розв’язання письмових вправ або:
1) як коментар готового розв’язання (із наступною само – або взаємоперевіркою);
2) як ігровий момент “Знайди помилку”.
III. Формулювання мети й завдань уроку
@ Після перевірки
IV. Актуалізація опорних знань
Виконання усних вправ
1. Які з формул задають лінійну функцію:
1) у = 12х – 10; 2) у = 4 – 0,5х; 3) у = 15х; 4) у = х(1 – х); 5) у = 11; 6) 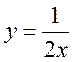 ; 7)
; 7) 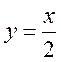 ?
?
2. Серед функцій: у = х + 0,5; у = -0,5х + 4; у = 5х – 1; у = 0,5x + 1; 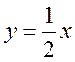 виберіть ті, графіки яких паралельні до графіка функції у = 0,5х + 1.
виберіть ті, графіки яких паралельні до графіка функції у = 0,5х + 1.
3. Виразіть змінну у через змінну х у рівнянні:
1) 7х – 2у = 6;
2) у – х2 = 9;
3) 3х + 0у = 5;
4) 1,5у + 0х = 5;
5) 4х – у = 0.
V. Вивчення нового матеріалу
@ Дослідження числа розв’язків системи двох лінійних рівнянь з двома змінними на основі графічних уявлень і знань, властивостей графіків лінійних функцій є основною дидактичною метою уроку.
Після повторення питань: а) що є графіком лінійної функції; б) яка умова різних випадків взаємного розташування графіків двох лінійних функцій та в) як із лінійного рівняння виразити у через х (див. попередній етап уроку) учням можна запропонувати практичні завдання.
1. У кожному з рівнянь системи 1) – 3) виразіть у через х та, використовуючи уявлення про властивості взаємного розташування графіків двох лінійних функцій, визначте (не виконуючи побудови), яке взаємне розташування графіків цих двох лінійних рівнянь:
1) 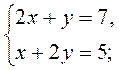 2)
2) 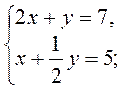 3)
3) 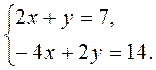
2. За взаємним розташуванням графіків визначте кількість розв’язків системи.
3. Знайдіть відношення коефіцієнтів 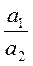 ,
, 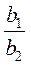 ,
, 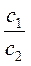 (рівнянь кожної системи) та порівняйте їх між собою.
(рівнянь кожної системи) та порівняйте їх між собою.
4. Порівняйте результати виконання п. З із висновками п. 2. Сформулюй те висновок.
Після виконання та обговорення результатів узагальнюємо та коригуємо висновки й заносимо відповідні записи в зошити.
Конспект 22 |
Кількість розв’язків системи лінійних рівнянь |
Нехай дано систему |
1) Якщо |
2) Якщо |
3) Якщо |
VI. Закріплення знань, вироблення вмінь
Виконання усних вправ
1. Скільки розв’язків має система, графіки рівнянь якої зображені на рис., якщо на рис. 2) прямі паралельні, на рис. 3) збігаються?
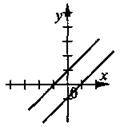
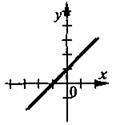
1)
2)
3)
2. Знайдіть відношення коефіцієнтів лінійних рівнянь системи 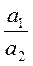 ,
, 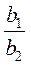 ,
, 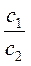 та порівняйте ці відношення.
та порівняйте ці відношення.
1) 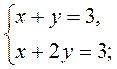 2)
2) 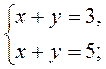 3)
3) 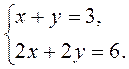
Виконання письмових вправ
1. Скільки розв’язків має система рівнянь:
1) 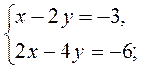 2)
2) 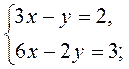 3)
3) 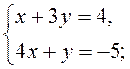 4)
4) 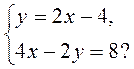
2. При яких значеннях а система 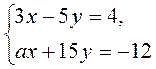
1) має нескінченно багато розв’язків? Знайдіть два такі розв’язки;
2) має один розв’язок? Знайдіть такий розв’язок;
Не має розв’язків?
3. При яких значеннях коефіцієнтів а і b розв’язком системи рівнянь 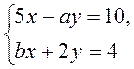 є пара чисел (2; -1)?
є пара чисел (2; -1)?
VII. Підсумки уроку
Серед рівнянь 2х + у = 3; 2х + 2у = 6 та 2х + 2у = 3 оберіть таке, щоб разом із рівнянням х + у = 3 вони утворили систему, що має:
1) один розв’язок; 2) безліч розв’язків; 3) не має розв’язків.
VIII. Домашнє завдання
№ 1. З’ясуйте, чи має система розв’язки та скільки. Для систем, що мають один розв’язок, відшукайте його, побудувавши графіки рівнянь:
1) 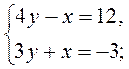 2)
2) 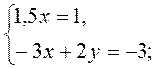 3)
3) 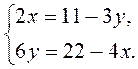
№ 2. Знайдіть які-небудь три розв’язки системи:
1) 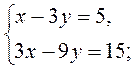 2)
2) 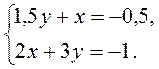
№ 3. На прямій, яка є графіком рівняння 4х + 9у = 1, узято точку, ордината якої дорівнює 1. Знайдіть абсцису цієї точки.
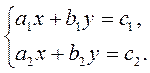
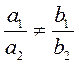 то система має один розв’язок (графіки рівнянь перетинаються).
то система має один розв’язок (графіки рівнянь перетинаються).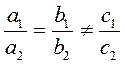 , то система не має розв’язків (графіки рівнянь паралельні).
, то система не має розв’язків (графіки рівнянь паралельні).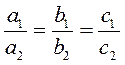 , то система має безліч розв’язків (розв’язком системи є будь-який розв’язок кожного з рівнянь) (графіки збігаються)
, то система має безліч розв’язків (розв’язком системи є будь-який розв’язок кожного з рівнянь) (графіки збігаються)