Головна ⇒ 📌Довідник з геометрії ⇒ Співнаправленість півпрямих
Співнаправленість півпрямих
Геометрія
Рух
Співнаправленість півпрямих
Дві півпрямі називаються Однаково напрямленими або Співнапрямленими, якщо вони суміщаються паралельним перенесенням (рисунок 1).
Теорема. Якщо півпрямі а і b однаково напрямлені й півпрямі b і c однаково напрямлені, то півпрямі а і c також однаково напрямлені.
Дві півпрямі називаються Протилежно напрямленими, якщо кожна з них однаково напрямлена з півпрямою, доповняльною до другої (рисунок 2).
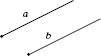
Рис. 1
a, b – співнапрямлені півпрямі
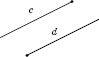
Рис. 2
c, d – протилежно напрямлені півпрямі
Related posts:
- Властивості перетворення подібності Геометрія Подібність фігур Властивості перетворення подібності Теорема 1. Перетворення подібності переводить прямі у прямі, півпрямі – у півпрямі, відрізки – у відрізки. Теорема 2. Перетворення подібності зберігає кути між півпрямими. Із цього випливає, що перетворення подібності переводить паралельні прямі в паралельні прямі. Дві фігури називаються Подібними, якщо вони переводяться одна в одну перетворенням подібності. Позначення: […]...
- Вектор. Модуль і напрям вектора. Рівність векторів УРОК № 42 Тема. Вектор. Модуль і напрям вектора. Рівність векторів Мета уроку: формування понять вектора, модуля вектора, напряму вектора; рівності векторів; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують вектор, модуль і […]...
- Перетворення в просторі – Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Перетворення в просторі Поняття перетворення для фігур у просторі означають так само, як і на площині (див. розділ “Геометрія. 8 клас”). Рухом Називається перетворення, при якому зберігаються відстані між точками. Властивості руху в просторі: Прямі переходять у прямі, півпрямі – у півпрямі, відрізки – у відрізки, кути між […]...
- Властивості руху Геометрія Рух Якщо кожну точку даної фігури змістити деяким чином, то дістанемо нову фігуру. Кажуть, що ця фігура утворюється перетворенням даної. Перетворення однієї фігури в іншу називається Рухом, якщо це перетворення зберігає відстань між точками. Властивості руху 1. Два рухи, виконані послідовно, дають знову рух. 2. Перетворення, обернене до руху, є рух. 3. Під час […]...
- Вектори в просторі (рівність векторів, колінеарність векторів, компланарність векторів). Додавання, віднімання векторів, множення вектора на число, властивості дій над векторами Урок 58 Тема. Вектори в просторі (рівність векторів, колінеарність векторів, компланарність векторів). Додавання, віднімання векторів, множення вектора на число, властивості дій над векторами Мета уроку: формування знань учнів про вектори в просторі, дії над векторами, заданими координатами, Формування вмінь застосовувати вивчений матеріал до розв’язування задач. Обладнання: схема “Вектори в просторі”. Хід уроку І. Перевірка домашнього […]...
- Рівність фігур Геометрія Рух Рівність фігур Дві фігури називаються Рівними, якщо вони переводяться рухом одна в одну. Теорема. Рівні трикутники (означення дивись у розділі “Геометрія.”) є рівними фігурами, тобто суміщаються рухом....
- Подібність просторових фігур – Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Подібність просторових фігур Перетворення фігури F називається Перетворенням подібності, якщо при цьому перетворенні відстані між точками змінюють себе в одну й ту саму кількість разів. Як і на площині, перетворення подібності в просторі переводить прямі у прямі, півпрямі у півпрямі, відрізки у відрізки і зберігає кути між півпрямими. […]...
- Скалярний добуток векторів Геометрія Вектори Скалярний добуток векторів Скалярним добутком векторів і називається число . Позначення: . . Очевидно, що . Розподільна властивість скалярного добутку: . Кутом між ненульовими векторами і називається кут BAC. Кутом між будь-якими двома ненульовими векторами і називається кут між векторами, що дорівнюють даним і мають спільний початок. Вважають, що кут між однаково напрямленими […]...
- Симетрія відносно точки Геометрія Рух Симетрія відносно точки Нехай O – фіксована точка, X – довільна точка площини. Відкладемо на продовженні відрізка OX за точку O відрізок , що дорівнює OX. Точка називається Симетричною точці X відносно точки O (див. рисунок). Очевидно, що точка, симетрична , є точка X. Перетворення фігури F у фігуру , при якому кожна […]...
- Подібність фігур Геометрія Подібність фігур Перетворення фігури F у фігуру називається Перетворенням подібності, якщо при цьому перетворенні відстані між точками змінюються в одну й ту саму кількість разів. Якщо відстані змінюються у k разів, то k називається Коефіцієнтом подібності. Якщо , перетворення подібності є рухом. Нехай F – дана фігура й О – фіксована точка. Через довільну […]...
- Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Візьмемо три взаємно перпендикулярні прямі Oх, Oy, Oz, які перетинаються в одній точці О (див. рисунок). Проведемо через кожну пару цих прямих площину. Площина, яка проходить через прямі Oх і Oу, називається площиною Oxy. Дві інші площини називаються відповідно Oxz і Oyz. Прямі Ox, Oy, Oz називаються Координатними […]...
- Паралельність прямих і площини Геометрія Стереометрія Паралельність прямих і площини Дві прямі в просторі називаються Паралельними, якщо вони лежать в одній площині й не перетинаються. Прямі, які не лежать в одній площині, називаються Мимобіжними. Зверніть увагу: “не лежать в одній площині” і “лежать у різних площинах” – це різні твердження. Наприклад, паралельні прямі a і b лежать у різних […]...
- Перпендикулярність площин Геометрія Стереометрія Перпендикулярність площин Дві площини, що перетинаються, називаються Перпендикулярними, якщо третя площина, перпендикулярна до прямої перетину цих двох площин, перетинає їх по перпендикулярних прямих (див. рисунок). Будь-яка площина, перпендикулярна до прямої перетину перпендикулярних площин, перетинає їх по перпендикулярних прямих. Ознака перпендикулярності площин Теорема 1. Якщо площина проходить через пряму, перпендикулярну до другої площини, то […]...
- Ознака паралельності площин Геометрія Стереометрія Ознака паралельності площин Теорема 1. Якщо дві прямі однієї площини, які перетинаються й відповідно паралельні двом прямим другої площини (див. рисунок), то ці площини паралельні. Теорема 2 (обернена). Якщо в одній площині є дві прямі, які перетинаються, і ці прямі паралельні другій площині, то такі площини паралельні. Зверніть увагу: прямі мають обов’язково перетинатися. […]...
- Паралельне перенесення та його властивості Геометрія Рух Паралельне перенесення та його властивості Перетворення фігури F, при якому довільна її точка з координатами переходить у точку , де a і b – одні й ті самі для всіх точок, називається Паралельним перенесенням. Теорема. Паралельне перенесення є рухом. При паралельному перенесенні пряма переходить у паралельну пряму (або в себе) (див. рисунок). Існування […]...
- Сила пружності. Закон Гука. Вага тіла. Невагомість МЕХАНІКА РОЗДІЛ 2. МЕХАНІЧНИЙ РУХ § 27. Сила пружності. Закон Гука. Вага тіла. Невагомість Запитання до вивченого 1. Сила пружності – це сила, що виникає внаслідок деформації тіла і напрямлена протилежно напряму переміщення частин тіла під час де формації. 2. Закон Гука: сила пружності прямо пропорційна деформації (видовженню) тіла (пружини) і напрямлена протилежно напрямку переміщення […]...
- Многогранники Геометрія Многогранники Двогранним кутом називається фігура, утворена двома півплощинами зі спільною прямою, що їх обмежує, – ребром двогранного кута. Півплощини називаються Гранями двогранного кута. Площина, перпендикулярна до ребра двогранного кута, перетинає його грані по двох півпрямих. Кут, утворений такими півпрямими, називається Лінійним кутом двогранного кута (див. рисунок). За міру двогранного кута приймається міра його лінійного […]...
- Розкладання вектора за координатними осями Геометрія Вектори Розкладання вектора за координатними осями Вектор називається Одиничним, якщо його абсолютна величина дорівнює одиниці. Одиничні вектори, які мають напрями додатних координатних півосей, називаються Координатними векторами, або Ортами (див. рисунок). Позначення: ; . Оскільки координатні вектори відмінні від нуля й неколінеарні, то будь-який вектор можна розкласти за цими векторами: ....
- Доцентрова і відцентрова сили ФІЗИКА Частина 1 МЕХАНІКА Розділ 2 ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ 2.9. Доцентрова і відцентрова сили Нехай тіло А рухається по колу радіуса r. У цьому разі розвиватиметься відцентрова сила Де – одиничний вектор, що збігається за напрямом із силою B. Відцентрова сила напрямлена протилежно доцентровій силі, що зумовлює викривлення траєкторії рухомого тіла. Доцентрова сила напрямлена до […]...
- Координати вектора УРОК № 43 Тема. Координати вектора Мета уроку: формування поняття координат вектора та вміння застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують координати вектора; застосовують вивчені означення і властивості до розв’язування задач. Хід уроку I. […]...
- Циліндр, описаний навколо кулі Геометрія Комбінації геометричних тіл Циліндр, описаний навколо кулі Площина, проведена через центр кулі паралельно твірним циліндра (рисунок нижче зліва), є площиною симетрії тіла. У цьому випадку висота циліндра дорівнює діаметру кулі. В осьовому перерізі цього тіла отримаємо прямокутник, у який вписане коло (рисунок справа). Але із цього випливає, що осьовий переріз даного циліндра – квадрат. […]...
- Геометричне місце точок Геометрія Основні властивості найпростіших геометричних фігур Геометричне місце точок Геометричним місцем точок (ГМТ), які мають певну властивість, називається така фігура, що складається з усіх точок площини, які мають цю властивість, і тільки з них. Довести, що фігура М є ГМТ, які мають властивість Р, означає довести два такі твердження. 1. Якщо точка А ∈ М, […]...
- Ознака паралельності прямої і площини Геометрія Стереометрія Ознака паралельності прямої і площини Теорема 1. Якщо пряма, яка не належить площині, паралельна якій-небудь прямій у цій площині, то вона паралельна і самій площині. Теорема 2. Якщо пряма паралельна площині, то на цій площині знайдеться пряма, яка паралельна даній прямій. Зверніть увагу: паралельність прямої і площини не означає, що ця пряма паралельна […]...
- Об’єми круглих тіл Геометрія Об’єми тіл Об’єми круглих тіл Об’єм циліндра (див. рисунок) дорівнює добутку площі його основи та висоти. ; . Об’єм конуса (див. рисунок) дорівнює одній третині добутку площі його основи та висоти. . . Об’єм зрізаного конуса (див. рисунок): ....
- Циліндр, вписаний у кулю Геометрія Комбінації геометричних тіл Циліндр, вписаний у кулю Основи циліндра є рівновіддаленими від центра кулі (рисунок нижче зліва). Ця комбінація тіл є симетричною відносно будь-якої площини, що проходить через центр кулі паралельно твірним циліндра. У перерізі тіла такою площиною дістанемо прямокутник і описане навколо нього коло (рисунок справа). Прямокутник ABCD є осьовим перерізом циліндра, а […]...
- Циліндр Геометрія Тіла обертання Циліндр Круговим циліндром називається тіло, яке складається з двох кругів, що не лежать в одній площині й суміщаються паралельними перенесенням, і всіх відрізків, що сполучають відповідні точки цих кругів (див. рисунок). Круги називаються Основами циліндра, а відрізки, що сполучають точки кіл кругів, – Твірними циліндра. Основи циліндра рівні й лежать у паралельних […]...
- Нерівність трикутника Геометрія Трикутники Нерівність трикутника Теорема. Які б не були три точки, відстань між будь-якими двома із цих точок не більша, ніж сума відстаней від них до третьої точки. Звідси випливає, що у будь-якому трикутнику кожна сторона менша за суму двох інших сторін, але більша за модуль різниці двох інших сторін. Якщо a, b і c […]...
- Конус, вписаний у кулю Геометрія Комбінації геометричних тіл Конус, вписаний у кулю Вершина конуса лежить на сфері (рисунок нижче зліва). Основа конуса лежить на сфері. Комбінація є симетричною відносно площини, що містить вісь конуса. У такому перерізі дістанемо трикутник, вписаний у коло (рисунок справа). Трикутник рівнобедрений. Бічні сторони – твірні конуса, коло – велике коло описаної кулі. Отже, радіус […]...
- ДІЯ МАГНІТНОГО ПОЛЯ НА РУХОМИЙ ЗАРЯД (СИЛА ЛОРЕНЦА) І ПРОВІДНИК ЗІ СТРУМОМ (СИЛА АМПЕРА). ПРАВИЛО ЛІВОЇ РУКИ Фізика підготовка до ЗНО комплексне видання ЕЛЕКТРОДИНАМІКА 4. МАГНІТНЕ ПОЛЕ. ЕЛЕКТРОМАГНІТНА ІНДУКЦІЯ 4.3. ДІЯ МАГНІТНОГО ПОЛЯ НА РУХОМИЙ ЗАРЯД (СИЛА ЛОРЕНЦА) І ПРОВІДНИК ЗІ СТРУМОМ (СИЛА АМПЕРА). ПРАВИЛО ЛІВОЇ РУКИ Напрям сили Лоренца визначається мнемонічним правилом лівої руки: якщо ліву руку розташувати так, щоб лінії В були напрямлені в долоню, чотири пальці показували напрям руху […]...
- Поворот Геометрія Рух Поворот Поворотом площини навколо даної точки називається такий рух, при якому кожний промінь, що виходить із даної точки, повертається на один і той самий кут в одному й тому самому напрямку (див. рисунок)....
« ГЕОЛОГІЯ