Степінь з натуральним показником
Урок № 20
Тема. Степінь з натуральним показником
Мета: розширити знання учнів відомостями про властивості степенів раціональних чисел з парним та непарним показником; сформувати вміння застосовувати ці властивості під час розв’язування вправ.
Тип уроку: застосування знань, умінь та навичок.
Хід уроку
І. Перевірка домашнього завдання
@ № 1-2 – вправи на відтворення вмінь, набутих на попередньому уроці, тому перевірку здійснюємо, перевіривши тільки відповіді (можна це зробити або зібравши зошити на перевірку, або,
II. Робота з випереджальним домашнім завданням
@ Роботу проводимо зазвичай за алгоритмом порівняння або робимо висновки, що приводять до формулювання властивостей степеня з парним та непарним показником.
III. Застосування знань
@ Після проведеного порівняння висновки щодо властивостей парного й непарного степеня є очевидними. Єдине, що може викликати труднощі,- це перехід від мовленнєвого формулювання до запису цих властивостей у вигляді тотожностей.
Тому,
– Як записати мовою математики:
1) а – додатне; 2) а – невід’ємне; 3) а – від’ємне; 4) а – не додатне.
– Як записати мовою математики число, протилежне до…?
– Яка формула парного числа? непарного числа? (Як записати мовою математики, що n – парне, n – непарне?)
Після цього в зошитах учні складають конспект:
Конспект 6 | |
Властивості степеня | |
1. Якщо n – парне число й а? 0, то аn? 0; якщо n – непарне й а? 0, то аn? 0. | |
2. n – парне (n = 2m) (-а)n = аn | N – непарне (n = 2m + 1) (-а)n = – аn |
IV. Засвоєння вмінь та навичок
@ Система завдань до уроку передбачає основну мету: закріпити знання властивостей степеня з парним та непарним показником і виробити вміння використовувати ці властивості під час розв’язування завдань різного змісту (від порівняння з нулем до доведення знака виразу, що містить степінь), а також удосконалити вміння, вироблені на попередньому уроці.
Виконання письмових вправ
1. Не обчислюючи, порівняйте значення виразів:
1) (-4,6)2 і 0; 2) 0 і (-2,7)3; 3) (-10)5 і (-8)4; 4) -66 і (-6)6.
2. Поясніть, чому при будь-яких значеннях змінної означення виразів
4х2 і (х – 8)2 є невід’ємними числами.
3. Доведіть, що вирази а2 + 1 та 3 + (5 – а)2 набувають лише додатних значень при будь-яких значеннях а.
4. Якого найменшого значення може набувати вираз:
1) х2 + 5;
2) х2 + 5;
3) (х + 5)2;
4) (х + 5)2 +5?
При якому значенні змінної це відбудеться?
5. Якого найбільшого значення може набувати вираз:
1) – х2 – 5;
2) – х2 + 5;
3) -(х + 5)2;
4) -(х – 5)2;
5) -(х – 5)2 – 5?
При якому значенні змінної це відбудеться?
6. Знайдіть значення виразу:
1) 14а2, якщо а = –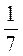 ;
;
2) 16 – с4, якщо с = -2;
3) (18х)4, якщо х = 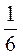 ;
;
4) х3 – х2, якщо х = 0,1;
5) (х + у)5, якщо х =-0,8; у = 0,6;
6) х5 + х4 + х3 + х2 + х + 1, якщо х = -1; 0; 10.
7*. Які з чисел: -3; -2; -1; 1; 2; 3 – є коренями рівняння:
1) х4 = 81;
2) х6 = 64;
3) х2 – х = 2;
4) х4 + х3 = 6х2;
5) х3 – 3х2 – 4х + 12 = 0;
6) х3 + 3х2 – х – 3 = 0.
V. Підсумки уроку. Рефлексія
1. Використовуючи вирази х2; х3; – х3; – х2; (-х)2; (-х)3 складіть якомога більше тотожностей. Поясніть.
2. Як би ви висловили двома словами зміст уроку?
VI. Домашнє завдання
№ 1. Запишіть у вигляді виразів:
1) квадрат суми чисел х та 1;
2) сума квадратів чисел а та b;
3) різниця куба числа т і квадрата числа n;
4) добуток четвертих степенів чисел а та b.
Знаки яких із записаних виразів ви можете встановити напевно?
№ 2. Обчисліть:
1) 102 – 32; 2) -62 – (-1)4; 3) 0,2 – 33 – 0,3 – 24.
№ 3*. Чому не має коренів рівняння: 1) х2 + 1 = 0; 2) х6 + х4 + х2 + 1 = 0?
№ 4. Випереджальне домашнє завдання. Спираючись на означення степеня:
1. Запишіть вираз, що тотожно дорівнює виразу а5; а3.
2. Яку з властивостей добутку можна використати, щоб помножити (а – а – а) на (а – а – а – а – а)?
3. Як записати утворений результат коротше?
4. Чи можна таким самим способом перетворити добуток а5 на b3? Чому?