Головна ⇒ 📌Довідник з геометрії ⇒ Сума кутів трикутника
Сума кутів трикутника
Геометрія
Основні властивості найпростіших геометричних фігур
Сума кутів трикутника
Теорема. Сума кутів трикутника дорівнює 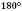 .
.
Із цієї теореми випливають наслідки:
1. У будь-якому трикутнику принаймні два кути гострі (тобто в трикутнику не може бути більше одного прямого або тупого кута).
2. Кути рівностороннього трикутника дорівнюють 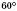 .
.
Зовнішнім кутом трикутника при даній вершині називається кут, суміжний із кутом трикутника при цій вершині (див. рисунок):
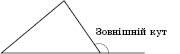
Властивості зовнішнього кута
Теорема 1. Зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів, не суміжних з ним.
Теорема 2. Зовнішній кут трикутника більший від будь-якого внутрішнього кута, не суміжного з ним.
Теорема 3. Сума зовнішніх кутів трикутника дорівнює 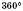 .
.
Related posts:
- СУМА КУТІВ ТРИКУТНИКА РОЗДІЛ 3 ТРИКУТНИКИ & 10. СУМА КУТІВ ТРИКУТНИКА Теорема 8 Сума кутів трикутника дорівняй: 180°. Доведення. Нехай ABC – довільний трикутник (мал. 130). Через йот вершину С проведемо пряму КР, паралельну стороні АВ. Утворені кути АСК і ВСР позначимо цифрами 1 і 2. Тоді ∠A = ∠1, ∠B = ∠2, як внутрішні різносторонні кути при […]...
- Ознаки паралельності прямих. Сума кутів трикутника Урок № 40 Тема. Ознаки паралельності прямих. Сума кутів трикутника Мета: перевірити рівень засвоєння знань та вмінь, передбачених програмою, із зазначених тем. Тип уроку: контроль та корекція знань. ХІД УРОКУ I. Організаційний момент II. Перевірка домашнього завдання Зібрати зошити з виконаною домашньою контрольною роботою. Роботу оцінити та врахувати в тематичному балі. III. Умова контрольної роботи […]...
- Сума кутів трикутника Урок № 34 Тема. Сума кутів трикутника Мета: закріпити знання учнів про зміст теореми про суму кутів трикутника та наслідків з неї; працювати над засвоєнням поняття “зовнішній кут трикутника”; розглянути властивість зовнішнього кута трикутника. Сформувати вміння: – знаходити на рисунку та виконувати зображення зовнішнього кута при даній вершині трикутника; – записувати теорему про зовнішній кут […]...
- Сума кутів трикутника. Нерівність трикутника § 3. Паралельні прямі. Сума кутів трикутника § 15. Сума кутів трикутника. Нерівність трикутника Вправи 357. Нехай х° – третій кут трикутника, тоді 35 + 96 + х = 180, звідси х + 131 = 180; х = 180 – 131; х = 49. Отже, третій кут дорівнює 49°. Відповідь: 49°. 358. Нехай х° – […]...
- Зовнішній кут трикутника та його властивості Розділ 3. Трикутники. Ознаки рівності трикутників § 18. Зовнішній кут трикутника та його властивості 438. ∠BAK – зовнішній кут при вершині А. 439. ∠LDP – зовнішній кут при вершині D. 441. ∠A + ∠B = 70° – за властивістю зовнішнього кута трикутника. 442. Зовнішній кут трикутника при вершині С дорівнює 74° згідно з властивістю зовнішнього […]...
- Властивості кутів трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 10. Властивості кутів трикутника 344. ∠E = 60°, ∠F = 40°, ∠D = 80°. ∠E + ∠F + ∠D = 60° + 40° + 80° = 180°. 345. На мал. 208 неправильно сказано градусну міру кутів? АВС, оскільки? ABC – прямокутний, a ∠B + ∠C = […]...
- Сума кутів опуклого многокутника Урок № 43 Тема. Сума кутів опуклого многокутника Мета: закріпити знання змісту понять, вивчених на попередньому уроці. Працювати над засвоєнням учнями змісту та доведення теореми про суму кутів опуклою многокутника. Сформувати вміння: – відтворювати зміст вивченої теореми; – застосовувати теорему під час розв’язування задач на знаходження градусної міри кутів многокутників. Тип уроку: засвоєння нових знань, […]...
- Порівняння сторін і кутів трикутника Урок № 37 Тема. Порівняння сторін і кутів трикутника Мета: перевірити рівень засвоєння навчального матеріалу теми “Прямокутні трикутники”; домогтися засвоєння учнями змісту та схеми доведення теореми про співвідношення між сторонами і кутами трикутника; сформувати вміння відтворювати формулювання теореми про співвідношення між сторонами і кутами трикутника та використовувати це співвідношення під час розв’язування задач. Тип уроку: […]...
- Суміжні й вертикальні кути Геометрія Основні властивості найпростіших геометричних фігур Суміжні й вертикальні кути Два кути називаються Суміжними, якщо в них одна сторона спільна, а інші сторони є доповняльними півпрямими. На рисунку і – суміжні. Властивості суміжних кутів Теорема 1. Сума суміжних кутів дорівнює . (Зверніть увагу: кути, сума яких дорівнює , не обов’язково суміжні.) Теорема 2. Коли два […]...
- Співвідношення між сторонами й кутом прямокутного трикутника Геометрія Трикутники Співвідношення між сторонами й кутом прямокутного трикутника Нехай ABC – прямокутний трикутник з прямим кутом С і гострим кутом при вершині A, що дорівнює . Косинусом гострого кута прямокутного трикутника називається відношення прилеглого катета до гіпотенузи. На рисунку або . Синусом кута називається відношення протилежного катета до гіпотенузи: або . Тангенсом кута називається […]...
- Опуклі чотирикутники. Сума кутів чотирикутника Урок № 2 Тема. Опуклі чотирикутники. Сума кутів чотирикутника Мета: сформувати уявлення про внутрішню область чотирикутника, поняття опуклого та неопуклого чотирикутників, кута опуклого чотирикутника, сусідніх та протилежних кутів опуклого чотирикутника. Сформувати первинні вміння: – відтворювати вивчені означення; – розрізняти на готових рисунках вивчені об’єкти; – зображувати вивчені об’єкти на рисунку. Сформувати усвідомлене розуміння змісту теореми […]...
- Тригранний і многогранний кути Геометрія Многогранники Тригранний і многогранний кути Нехай промені a, b, c виходять з однієї точки й не лежать в одній площині. Тригранним кутом називається фігура, яка складається з трьох плоских кутів , , (див. рисунок). Ці кути називаються Гранями тригранного кута, а їх сторони – Ребрами. Спільна вершина плоских кутів називається Вершиною тригранного кута. Двогранні […]...
- Властивості й ознака рівнобедреного трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 12. Властивості й ознака рівнобедреного трикутника 476. На мал. 72: ML і МК – бічні сторони, KL – основа, ∠K = ∠L. 477. KD = DF, КЕ = EF, ∠K = ∠F, ∠KDE = ∠FDE, ∠DEK = ∠DEF = 90°. 478. Щоб провести бісектрису, медіану і […]...
- Прямокутний трикутник Геометрія Основні властивості найпростіших геометричних фігур Прямокутний трикутник Трикутник називається Прямокутним, якщо він має прямий кут. Сторона, яка лежить проти прямого кута, називається Гіпотенузою. Сторони, що утворюють прямий кут, називаються Катетами. На рисунку – прямокутний. AB і BC – катети, AC – гіпотенуза. Теорема. Сума гострих кутів прямокутного трикутника дорівнює . Ознаки рівності прямокутних трикутників […]...
- Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 19. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників 466. 1) PF – гіпотенуза, PL і LF – катети. 2) PF довша за PL, PF довша за LF, оскільки PF – гіпотенуза. 467. На рис. 321 трикутники рівні за двома катетами. Оскільки АС = ML, СВ = LP, […]...
- Кут. Вимірювання кутів. Бісектриса кута Розділ 1. Елементарні геометричні фігури та їхні властивості § 3. Кут. Вимірювання кутів. Бісектриса кута 33. 1) М – вершина кута, МА і МК – сторони кута АМК; 2) L – вершина кута, LP і LF – сторони кута PLF; 3) N – вершина кута, NB i NC – сторони кута BNC. 34. 1) O […]...
- Вимірювання кутів. Види кутів УРОК 36 Тема. Види кутів. Вимірювання кутів Мета: систематизувати знання учнів про поняття кута, його елементів, позначення, вимірювання і класифікацію; вдосконалювати вміння і відпрацьовувати навички вимірювання кутів, визначати видів кутів і розв’язувати задачі на застосування аксіоми вимірювання кутів. Тип уроку: застосовування знань, вмінь та навичок. Обладнання: таблиця “Кути. Вимірювання кутів”. Хід уроку I. Перевірка домашнього […]...
- НЕРІВНОСТІ ТРИКУТНИКА РОЗДІЛ 3 ТРИКУТНИКИ & 15. НЕРІВНОСТІ ТРИКУТНИКА Ви вже знаєте, що кожна сторона трикутника менша від суми двох інших його сторін. Щоб довести це твердження як теорему, спочатку розглянемо іншу теорему. Теорема 19 У кожному трикутнику проти більшої сторони лежить більший кут, а проти більшого кута – більша сторона. Доведення. 1) Нехай у трикутнику ABC […]...
- Ознаки рівнобедреного трикутника Геометрія Основні властивості найпростіших геометричних фігур Ознаки рівнобедреного трикутника Теорема 1. Якщо в трикутнику два кути рівні, то він рівнобедрений. Теорема 2. Трикутник рівнобедрений, якщо: – одна з його висот є медіаною; – одна з його медіан є бісектрисою; – одна з його висот є бісектрисою. Теорема 3. Трикутник рівнобедрений, якщо: – дві його висоти […]...
- Висота, бісектриса, медіана трикутника Геометрія Основні властивості найпростіших геометричних фігур Висота, бісектриса, медіана трикутника Висотою Трикутника, опущеною з даної вершини, називається перпендикуляр, проведений із цієї вершини до прямої, що містить протилежну сторону трикутника. У кожному трикутнику можна провести три висоти. Висоти трикутника (або прямі, що їх містять) перетинаються в одній точці. На рисунках зображено, як перетинаються висоти в гострокутному […]...
- Види кутів. Вимірювання кутів УРОК 35 Тема. Вимірювання кутів. Види кутів Мета: ознайомити учнів із поняттям порівняння кутів і їх видами залежно від величини кутів; навчити розпізнавати прямі, гострі і тупі кути на рисунку та визначати вид кута за його градусною мірою. Тип уроку: застосування знань, навичок та вмінь. Обладнання: демонстраційний транспортир; таблиця-схема “Кути. Види кутів”, різнокольорові моделі розгорнутого […]...
- Рівносторонній трикутник – ТРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ТРИКУТНИКИ Рівносторонній трикутник Усі висоти, медіани й бісектриси мають однакову довжину. Вписане і описане коло мають спільний центр. Середня лінія трикутника – відрізок, що сполучає середини двох сторін трикутника. Теорема: Зовнішній кут трикутника – кут, суміжний із внутрішнім кутом трикутника. Теорема: Теорема косинусів: у будь-якому трикутнику зі сторонами а, b, с […]...
- Рівносторонній трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівносторонній трикутник Якщо всі сторони трикутника рівні, він називається Рівностороннім. На рисунку . Теорема 1. У рівносторонньому трикутнику всі кути рівні. Теорема 2. У рівносторонньому трикутнику висота, медіана, бісектриса, проведені з однієї вершини, збігаються. Теорема 3. У рівносторонньому трикутнику всі медіани (висоти, бісектриси) рівні між собою....
- Теорема косинусів Геометрія Розв’язування трикутників Теорема косинусів Теорема (косинусів). Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін і косинуса кута між ними. У трикутнику, зображеному на рисунку, за теоремою косинусів: . Теорему косинусів зручно застосувати для розв’язування таких задач. 1. Знайти сторону трикутника, якщо відомі дві інші сторони й кут […]...
- Кути, вписані в коло Геометрія Кути, пов’язані з колом Кути, вписані в коло Кут розбиває площину на дві частини. Кожна із цих частин називається Плоским кутом. Плоскі кути із спільними сторонами називаються Доповняльними. Якщо плоский кут є частиною півплощини, то його градусною мірою називається градусна міра звичайного кута з тими самими сторонами. Центральним кутом у колі називається плоский кут […]...
- Бісектриса Геометрія Основні властивості найпростіших геометричних фігур Бісектриса Бісектрисою кута називається промінь, який виходить із вершини кута, проходить між його сторонами й ділить кут пополам. На рисунку BD – бісектриса . Властивості бісектриси Теорема 1. Бісектриса кута утворює з його сторонами кути, не більші за . Теорема 2. Бісектриси вертикальних кутів лежать на одній прямій (тобто […]...
- Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника Розділ 3. Трикутники. Ознаки рівності трикутників § 15. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника 351. 1) AT – висота трикутника ABC. 2) AN – медіана трикутника ABC. 3) АР – бісектриса трикутника? AВС. 352. Оскільки AK – висота, то ∠BKA = ∠CKA = 90°. 353. Оскільки АК – бісектриса, то ∠BAK = […]...
- Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною Розділ 2. Взаємне розміщення прямих па площині § 10. Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною 199. 1) ∠1 = ∠8, ∠6 = ∠3 (як відповідні кути при паралельних прямих а і b і січній с). 2) ∠2 = ∠4 (як внутрішні різносторонні кути при паралельних прямих а і b і […]...
- Кути трикутника і чотирикутника Урок № 50 Тема: Кути трикутника і чотирикутника Мета. Познайомити учнів з видами кутів і трикутників в залежності від кутів, які входять до кута. Навчити учнів вимірювати кути за допомогою транспортира. Формувати уміння і навички розв’язувати геометричні задачі. Розвивати логічне мислення учнів, шляхом розв’язування задач, продовжувати формувати вміння працювати з підручником. Форми роботи: бліцопитування, робота […]...
- Теорема синусів Геометрія Розв’язування трикутників Теорема синусів Теорема 1 (синусів). Сторони трикутника пропорційні до синусів протилежних кутів. У трикутнику, зображеному на рисунку, за теоремою синусів маємо: . Теорема 2. Якщо R – радіус кола, описаного навколо трикутника, то , або , де a – сторона трикутника, а – протилежний цій стороні кут. Теорема 3. У трикутнику проти […]...