Сума кутів трикутника. Нерівність трикутника

§ 3. Паралельні прямі. Сума кутів трикутника

§ 15. Сума кутів трикутника. Нерівність трикутника

Вправи

357. Нехай х° – третій кут трикутника, тоді 35 + 96 + х = 180, звідси х + 131 = 180; х = 180 – 131; х = 49. Отже, третій кут дорівнює 49°.

Відповідь: 49°.

358. Нехай х° – один із кутів трикутника, тоді інші кути дорівнюють: 3x° та (х + 35)°. Маємо рівняння: х + 3х + х + 35 = 180, тоді 5х + 35 = 180; 5х = 180 – 35; 5х = 145; х = 29, звідси 3х = 3 х 29 = 87, x + 35 = 29 + 35 = 64. Отже, кути трикутника дорівнюють 29°, 87°, 64°.

Відповідь: 29°, 87°, 64°.

359. Нехай кути трикутника

дорівнюють 2х°, 3х°, 7х°. Тоді 2х + 3х + 7х = 180, звідси 12х = 180; х = 180 : 12; х = 15. Тоді 2х = 2 х 15 = 30, 3х = 3 х 15 = 45, 7x = 7 х 15 = 105. Отже, куги трикутника дорівнюють 30°, 45° і 105°.

Відповідь: 30°, 45° і 105°.

360. Оскільки всі кути рівностороннього трикутника рівні, то кожний кут дорівнює 180°: 3 = 60°.

Відповідь: 60°, 60°, 60°.

361. Нехай х° – гострий кут прямокутного рівнобедреного трикутника, Тоді 90° + 2х° = 180°, звідси 2х = 180 – 90; 2х = 90; х = 90 : 2; х = 45. Отже, кути прямокутного рівнобедреного трикутника дорівнюють 45°, 90°, 45°.

Відповідь: 45°, 90°, 45°.

362. Нехай х° – кут при вершині рівнобедреного трикутника,

тоді х + 2 х 63 = 180, звідси х + 126 = 180; х = 180 – 126; х = 54°. Отже, кут при вершині рівнобедреного трикутника дорівнює 54°.

Відповідь: 54°.

363. Нехай х° – кут при основі рівнобедреного трикутника, тоді 2х + 104 = 180, звідси 2х = 180 – 104; 2х = 76; х = 76 : 2; х = 38. Отже, кути при основі рівнобедреного трикутника дорівнюють 38° і 38°.

Відповідь: 38° і 38°.

364. Нехай х° – кут при основі рівнобедреного трикутника, тоді 4х + х + х = 180, звідси 6х = 180; х = 180 : 6; x = 30. 4x = 4 х 30 = 120. Отже, кути трикутника дорівнюють 30°, 30°, 120°.

Відповідь: 30°, 30°, 120°.

365. Нехай х° – кут при основі рівнобедреного трикутника, х° + 48° – кут при вершині, тоді 2х + (х + 48) =180, звідси 3х + 48 = 180; 3х = 180 – 48; 3х = 132; х = 132 : 3; х = 44. х + 48 = 44 + 48 = 92. Отже, кути трикутника дорівнюють 44°, 44°, 92°.

Відповідь: 44°, 44°, 92°.

366. 1) Кут при основі не може дорівнювати 110°, бо 110° х 2 = 220° > 180°. Тому це кут при вершині. Якщо х° – кут при основі, то 110 + 2х = 180, звідси 2х = 180 – 110; 2х = 70; х = 70 : 2;х = 35. Отже, кути трикутника дорівнюють 35°, 35°, 110°.

Відповідь: 35°, 35°, 110°; один розв’язок.

2) Якщо 50° – кут при основі, а х° – кут при вершині рівнобедреного трикутника, то 2 х 50 + х = 180, звідси 100 + х = 180; х = 180 – 100; х = 80. Якщо 50° – кут при вершині, а х° – кут при основі рівнобедреного трикутника, то 50 + 2х = 180°; звідси 2х = 180 – 50; 2х = 130; х = 130 : 2; х = 65.

Отже, кути трикутника дорівнюють 50°, 50° і 80° або 65°, 65° і 50°.

Відповідь: 50°, 50° і 80° або 65°, 65° і 50°; два розв’язки.

367. 1) Якщо 42° – кут при основі, х° – кут при вершині, тоді 2 х 42 + х = 180, звідси 84 + х = 180; х = 180 – 84; х = 96. Отже, кути трикутника дорівнюють 42°, 42°, 96°.

Якщо 42° – кут при вершині, х° – кут при основі, тоді 42 + 2х = 180, звідси 2х = 180 – 42; 2х = 138; х = 138 : 2; х = 69. Отже, кути трикутника дорівнюють 42°, 69°, 69°.

Відповідь: 42°, 42°, 96° або 42°, 69°, 6°; два розв’язки.

2) Кут при основі не може дорівнювати 94°, бо 94° х 2 = 188° > 180°. Тому це кут при вершині. Якщо х° – кут при вершині, то 2х + 94 = 180, звідси 2х = 180 – 94; 2х = 86; х = 86 : 2; х = 43. Отже, кути трикутника дорівнюють 43°, 43°, 94°.

Відповідь: 43°, 43°, 94°; один розв’язок.

368. 1) Сторони трикутника не можуть дорівнювати 6 см, 5 см, 12 см, бо 12 > 5 + 6 – не виконується нерівність трикутника.

Відповідь: не можуть.

2) Сторони трикутника не можуть дорівнювати 6 см, 5 см, 11 см, бо 11 = 5 + 6 – не виконується нерівність трикутника.

Відповідь: не можуть.

369. На рисунку ∠BAC = 2 х ∠BAK = 2 х 18° = 36°.

∠ABC = 180° – (90° + 36°) = 54°. ∠AKC = 180° – (90°+ 18°) = 72°.

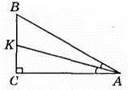
Відповідь: 72°, 54°.

370. На рисунку AB = BC, ∠ACK = ∠KCB, ∠A = 66°.

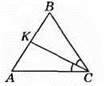
Відповідь: 81°.

371. На рис. ∠ACM = ∠MCB, ∠CAK = ∠KAB, ∠BAC = 116°, ∠BCA = 34°.

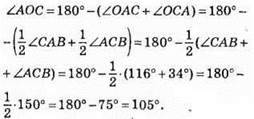
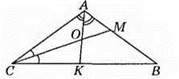
Відповідь: 105°.

372. На рис. ∠B = 36°, ∠BAD = ∠DAC.

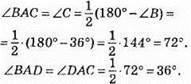
Таким чином, ∠DAB = ∠B, отже, ?ADB – рівнобедрений.

∠ADC = 180° – (∠DAC + ∠DCA) = 180° – (36° + 72°) = 180° – 108° = 72°.

Таким чином, ∠ADC = ∠C, отже, ?CAD – рівнобедрений.

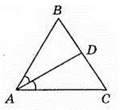
373. На рисунку ∠ABF = ∠FBC, ∠A = 39°, ∠AFB = 78°.

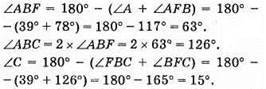
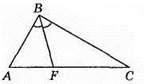
Відповідь: 15°.

374. Нехай α, β, γ – кути трикутника. Тоді α + β + γ = 180° і α = β + γ, тоді α + β + γ = α + (β + γ) = α + α = 2α, звідси 2α = 180°, α = 180° : 2, α = 90°. Отже, трикутник – прямокутний.

375. 1) ∠KEM, ∠NFM; 2) ∠MEF.

376. 1) ?АМС; 2) ?АМВ, ?CMD.

377. 1) ∠ACB = 180° – ∠BCD = 180° – 75° = 105°.

2) ∠A – ∠B = 180° – 105° = 75°.

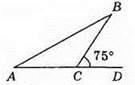
Відповідь: 1) 105°; 2) 75°.

378. Так (якщо трикутник тупокутний).

379. Трикутник прямокутний.

380. ∠DCB = 136°, ∠B = 61°, тоді ∠A = ∠BCD – ∠B = 136° – 61° = 75°.

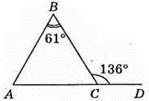
Відповідь: 75°.

381. ∠BCD = 154°. Нехай ∠B = х°, ∠A = х° + 28°, тоді х + х + 28 = 154, звідси 2х + 28 = 154; 2х = 154 – 28; 2х = 126; х = 126 : 2; х = 63, тоді x + 28 = 63 + 28 = 91.

Отже, шукані кути дорівнюють 63°, 91°.

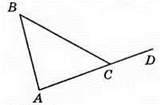
Відповідь: 63°, 91°.

382. Нехай ∠A = х°, ∠B = 6х°, тоді х + 6х = 98, звідси 7x = 98; х = 98 : 7; х = 14, тоді 6х = 6 х 14 = 84. Отже, шуані кути дорівнюють 14° і 84°.

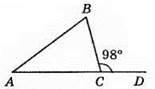
Відповідь: 14°, 84°.

383. AB = BC, ∠DBA. Оскільки ∠A = ∠C, ∠A + ∠C = 38°, тоді ∠A = ∠C = 38° : 2 = 19°. ∠B= 180° – 38° = 142°.

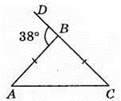
Відповідь: 19°, 19°, 142°.

384. 1)Оскільки АВ > АС > ВС, тоді ∠С > ∠B > ∠A.

2) Оскільки AB = BC, BC > АС, тоді ∠C = ∠A > ∠B.

385. Якщо ∠A = 34°, ∠B = 28°, тоді ∠C = 180° – 34° – 28° = 118°.

Оскільки ∠B < ∠A < ∠C, то АС < BC < AB.

386. 1) Оскільки ∠C > ∠A > ∠B, тоді АВ > ВС > АС.

2) Оскільки ∠B > ∠C, ∠A = ∠B, тоді BC = АС > AB.

387. Нехай ∠A = ∠A1, ∠B = ∠B1, тоді ∠C = 180° – (∠A + ∠B) = 180° – (∠A1 + ∠B1) = ∠C1. Отже, ∠C = ∠C1.

388. 1) Відповідний кут трикутника дорівнює 180° – 54° = 126°. Це може бути тільки кут при вершині (бо він тупий). Тоді кут при основі дорівнює 1/2 • 54° = 27°. Отже, кути трикутника дорівнюють 27°, 27°, 126°.

Відповідь: 27°, 27°, 126°; один розв’язок.

2) Якщо 112° – зовнішній кут при основі, то відповідний кут трикутника дорівнює 180° – 112° = 68°, і тоді кут при вершині дорівнює 180° – 68° – 68° = 44°. Отже, кути трикутника дорівнюють 68°, 68°, 44°.

Якщо 112° – зовнішній кут при вершині рівнобедреного трикутника, то відповідний кут трикутника дорівнює 180° – 112° = 68°, а кут при основі дорівнює 1/2 • 112° = 56°. Отже, кути трикутника дорівнюють 56°, 56°, 68°.

Відповідь: 44°, 68°, 68° або 56°, 56°, 68°; два розв’язки.

389. Якщо це зовнішній кут при основі, то відповідний кут трикутника дорівнює 180° – 130° = 50°, а кут при вершині 180° – 2 х 50° = 80°. Отже, кути трикутника дорівнюють 50°, 50°, 80°.

Якщо це зовнішній кут при вершині, то відповідний кут трикутника дорівнює 180° – 130° = 50°, а кут при основі 1/2 • 130° = 65°. Отже, кути трикутника дорівнюють 65°, 65°, 50°.

Відповідь: 50°, 50°, 80° або 50°, 65°, 65°; два розв’язки.

390. 1) Якщо одна сторона трикутника дорівнювала б 20 см, тоді сума двох сторін дорівнювала б 30 см – 20 см = 10 см, і нерівність трикутника не виконувалася, бо 20 > 10. Отже, сторона не може дорівнювати 20 см.

2) Якщо одна сторона трикутника дорівнювала б 15 см, тоді сума двох сторін дорівнювала б 30 см – 15 см = 15 см, і нерівність трикутника не виконувалася б, бо 15 = 15. Отже, сторона не може дорівнювати 15 см.

391. 1) Якщо дві сторони трикутника дорівнюють 7 см і 9 см, то третя сторона дорівнює 20 – 7 – 9 = 4 (см). Трикутник ні сторонами 7 см, 9 см, 4 см існує. Отже, периметр трикутника може дорівнювати 20 см.

2) Якщо дві сторони дорівнюють 7 см і 9 см, то третя сторона дорівнює 32 – 7 – 9 = 16. Трикутника зі сторонами 7 см, 9 см, 16 см не існує, бо не виконується нерівність трикутника, бо 7 см + 9 см = 16 см. Отже, периметр трикутника не може дорівнювати 16 см.

3) Якщо дві сторони дорівнюють 7 см i 9 см, то третя сторона дорівнює 18 – 9 – 7 = 2 (см). Трикутник зі сторонами 2 см, 7 см, 9 см не існує, бо 2 + 7 = 9. Отже, периметр не може дорівнювати 18 см.

392. Нехай х см, х + 2 см, х + 6 см. Тоді х + х + 2 + х + 6 = 20, звідси 3х + 8 = 20; 3х = 20 – 8; 3х = 12; х = 12 : 3; х = 4. Тоді сторони трикутника дорівнюють 4 см, 6 см і 10 см. Проте трикутника зі сторонами 4 см, 6 см, 10 см не існує (бо 10 = 4 + 6).

Відповідь: ні.

393. ∠AOC = 180° – (∠OAC + ∠OCA) = 180° – ∠BAC = ∠BAD. Отже, ∠AOC дорівнює зовнішньому куту трикутника ABC при вершині А.

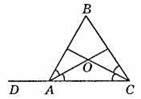
394. Оскільки ВС || AD, то ∠B = ∠D, тоді ∠CMD = ∠A + ∠MDA = ∠A + ∠B = 25° + 55° = 80°.

Відповідь: 80°.

395. AB = АС, ∠AKB = 105°. ∠AKB – зовнішній кут трикутника ВКС. Якщо ∠KBC = x°, тоді ∠C = 2x° i x + 2x = 105, звідси 3х = 105; х = 105 : 3; х = 35, 2х = 70. Отже, ∠C = 70°, ∠ABC = 70°, ∠A= 180° – 70° – 70° = 40°.

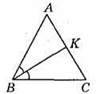
Відповідь: 40°, 70°, 70°.

396. BD = ВС, ∠ACD = 15°, ∠DCB = 40°. Оскільки ∠DCB = 40° і DB = ВС, то ∠CDB = 40°, ∠B = 180° – 40° – 40° = 100°.

Оскільки ∠BDC – зовнішній кут трикутника ADC при вершині D і ∠ACD = 15°, тоді ∠BDC = ∠A + ∠ACD, звідси 40° = ∠A + 15°, ∠A = 40° – 15°, ∠A = 25°. ∠C = 180° – ∠A – ∠B = 180° – 25° – 100° =55°.

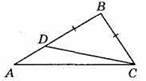
Відповідь: 100°, 25°, 55°.

397. ∠3 = 180° – ∠B = ∠1 = 180° – ∠B – ∠2 = ∠4. Отже, ∠3 = ∠4.

398. ∠CAD = 180° – ∠ACD – ∠D = 180° – 95° – 45° = 40°.

Оскільки ВС || AD, то ∠CAD = ∠BCA = 40° (як внутрішні різносторонні при паралельних прямих ВС і AD та січній АС).

∠BAC = 180° – ∠B – ∠BCA = 180° – 100° – 40° = 40°.

Оскільки ∠BAC = ∠BCA = 40°, то? ABC – рівнобедрений і AB = ВС.

399. ∠CAK = 180° – ∠BAC = 180° – 70° = 110°.

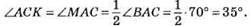
∠AKC = 180° – (110° + 35°) = 35°.

Відповідь: 35°, 35°, 110°.

400.

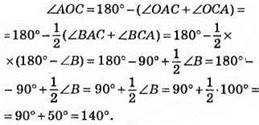
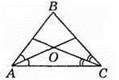
Відповідь: 140°.

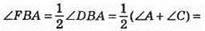
401. 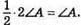Оскільки ∠FBA = ∠A і ці кути є різносторонні при прямих FB і АС та січній AB, то FB || АС.

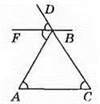
402. Нехай FB || АС, тому ∠FBA = ∠BAC – як внутрішні різносторонні при паралельних прямих FB і АС та січній AB. Отже, ∠DBA = 2∠ВАС, але ∠DBA = ∠ВАС + ∠BCA, тоді 2∠BAC = ∠BAC + ∠BCA, 2∠BAC – ∠BAC = ∠BCA; ∠BAC = ∠BCA. Оскільки ∠BAC = ∠BCA, то? ABC – рівнобедрений (AB = BC).

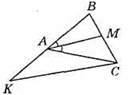
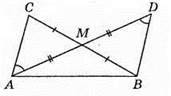
403. ∠BAC = ∠C = 2∠B. Тоді ∠B + 2 • 2∠B = 180° або 5∠B = 180°, звідси ∠B = 180°: 5, ∠B = 36°.

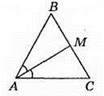
∠BAC – ∠C = 72°; ∠BAM = 1/2 • ∠BAC = 1/2 • 72° = 36°. ∠B = ∠BAM, отже, BM = MA. ∠AMC = 180° – (∠MAC + ∠C) = 180° – (36° + 72°) = 180° – 108° = 72°; ∠AMC = ∠C, отже, MA = АС. ОскількиBM = MA, MA = АС, то BM = AC.

404. BM = AM = AC. Оскільки AM = AC, то ∠C = ∠AMC = ∠B + ∠BAM, але BM = AM, тому ∠B = ∠BAM. Отже, ∠C = ∠BAC = 2∠B, тоді ∠B + 2 • 2∠B = 180°; 5∠B = 180°; ∠B = 180° : 5; ∠B = 36°, ∠BAC= ∠C = 72°.

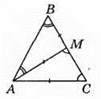
Відповідь: 36°, 72°, 72°.

405. 2) Якщо б усі кути були меншими від 60°, то їхня сума була б менша за 180°, чого не може бути. Отже, в будь-якому трикутнику є кут, не менший за 60°.

2) Якщо б усі кути були більшими від 60°, то їх сума була б більша за 180°, чого не може бути. Отже, в будь-якому трикутнику є кут, не більший за 60°.

406. 1) Нехай α > β + γ, тоді α + α > α + β + γ або 2α > 180°, звідси α > 180° : 2; α > 90°. Отже, якщо один із кутів трикутника більший за суму двох інших, то даний трикутник – тупокутний.

Відповідь: тупокутний.

2) Нехай α – будь-який кут трикутника, тоді α < β + γ, тоді α + α < α + β + γ або 2α < 180°, звідси α < 90°. Отже, якщо будь-який з кутів трикутника менший від суми двох інших, то даний трикутник – гострокутний.

Відповідь: гострокутний.

407. Нехай α, β, γ – кути трикутника. Оскільки α + β > 90°, то γ = 180° – (α + β) < 180° – 90° = 90°. Аналогічно, α < 90°, β < 90°. Отже, трикутник – гострокутний.

Відповідь: гострокутний.

408. ∠DAC = ∠B + ∠ACB > ∠B > 90°. ∠ADC = 180° – (∠DAC + ∠ACD) < 90°, тобто ∠ADC < ∠DAC.

У? DAC сторона АС лежить напроти ∠ADC, а сторона CD – напроти більшого кута DAC. Тому CD > АС.

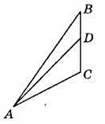
409. ∠C > 90°; ∠ADC = 180° – (∠C + ∠CAD) < 90°, отже, ∠C > ∠ADC.

У? ADC сторона АС лежить напроти ∠ADC, а сторона AD – напроти більшого кута С, тому AD > АС.

410. Нехай ∠CAM = ∠MAB, ∠CBN = ∠NBA, ∠AOB = 90°. Тоді ∠C = 180° – (∠CAB + ∠CBA) = 180° – (2∠OAB + 2∠OBA) = 180° – 2(∠OAB + ∠OBA) = 180° – 2(180° – ∠OAB) = 180° – 2(180° – 90°) = 180° – 2 • 90° = 180° = 180° = 0°, такого бути не може. Отже, не існує трикутника, дві діагоналі якого перпендикулярні.

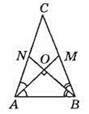
Відповідь: не існує.

411. ∠BAL = ∠LAC, ∠ACK = ∠KCB, AO = OL.

Оскільки СО – бісектриса і медіана трикутника ALC, тоді ∠AOC = 90°, що неможливо (див. задачу 410). Отже, не Існує трикутника, у якого одна бісектриса ділить навпіл другу бісектрису.

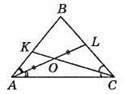
Відповідь: не існує.

412. 1-й випадок. Нехай ∠ABL = ∠LBC, AL = BL = CL.

Оскільки BL – бісектриса і медіана трикутника ABC, то BL ⊥ АС. Тоді ∠ALB = ∠BLC = 90°, 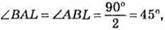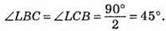Отже, кути трикутника дорівнюють 45°, 45°, 90°.

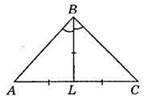
2-й випадок. ∠ABL = ∠LBC, AL = BL, BL = ВС.

Нехай ∠ABC = 2x°, тоді ∠A = х°, 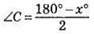і для? АВС маємо: 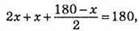звідси 4х + 2х + 180 – х = 360; 5х = 180; x = 180 : 5; x = 36, тоді ∠B = 72°, 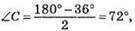∠A = 36°. Отже, кути трикутника дорівнюють 36°, 72°, 72°.

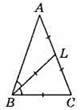
Відповідь: 45°, 48°, 90° або 36°, 72°, 72°.

413. Припустимо, що точка С не є внутрішньою точкою відрізка, тоді точка С лежить на прямій AB поза відрізком AB або точка С не належить прямій AB.

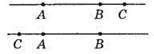
Розглянемо випадок, коли С лежить на прямій AB, але не належить відрізку AB, тоді не виконується рівність AB = АС + СВ. Отже, точка С не може належати прямій AВ і не належати відрізку AB.

Якщо точка С не належить прямій AB, то виконується нерівність AВ < АС + ВС, що суперечить умові. Отже, точка С не може лежати поза прямою AB.

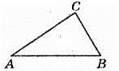
Таким чином, точка С – внутрішня точка відрізка AB.

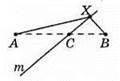
414. Якщо шукана точка X лежить десь на прямій m, тоді згідно з нерівністю трикутника АХ + ХВ > AB. Сума АХ + ХВ буде найменшою, коли точка X буде належати відрізку AB. Отже, С – точка перетину відрізка AB і прямої m.

415. Якщо одна сторона дорівнює 2,8 см, а друга сторона – 0,6 см, тоді третя сторона – x см, причому 2,8 – 0,6 < х < 2,8 + 0,6, звідси 2,2 < х < 3,4. Отже, х = 3. Отже, третя сторона дорівнює 3 см.

Відповідь: 3 см.

416.

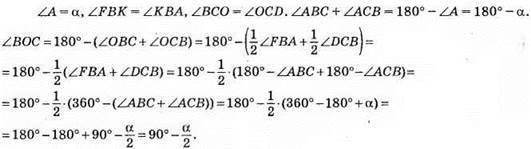
Відповідь: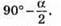

417. CM = MB, ∠CAM > ∠BAM.

На продовженні медіани AM за точку M відкладемо відрізок MD, який дорівнює AM. Тоді? САМ = ?BDM (за двома сторонами і кутом між ними), звідси ∠CAM = ∠BDM, АС = BD.

У? ADB: ∠ADB > ∠BAD, тоді AB > BD = АС. Отже, AB > АС.

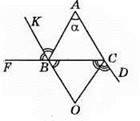
418. Нехай ∠B = β, тоді ∠EFB = β, ∠AEF = ∠EBF + ∠EFB = β + β = 2β i ∠EAF = 2β. Нехай ∠C = γ, тоді ∠FAC = 180° – 2∠C = 180° – 2γ.

Оскільки ∠EAF + ∠FAC = ∠C, то 2β + 180° – 2γ = γ, звідси 2β + 180° = 3γ.

З іншого боку βγ= 180° – 2у, тоді 2(180° – 2γ) + 180° = 3γ; 360° – 4γ + 180° = 3γ; 7γ = 540°; γ = (540/7)°.

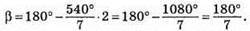
Отже, кути трикутника дорівнюють: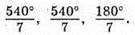

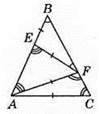
419. AB = 2 см, ∠A = 60°, ∠B = 70°, AD = 1 CM. Середину M сторони AB з’єднаємо з точкою D. ?AMD – рівносторонній, отже, ∠AMD = ∠MDA = 60°. ?BMD – рівнобедрений, тому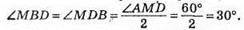

Тоді ∠DBC = 70° – ∠DBA = 70° – 30° = 40°. ∠ADB = ∠ADM + ∠MDB = 60° + 30° = 90°, тоді ∠BDC = 90°. ∠C = 180° – ∠DBC – ∠BDC = 180° – 40° – 90° = 50°. Отже, кути трикутника BDCдорівнюють 40°, 90°, 50°.

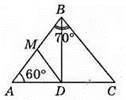
Відповідь: 40°, 90°, 50°.

420. AM = MC. Доведемо, що AB + BC > 2 BM.

На промені ВМ від точки М відкладемо MD = ВМ. ?AMD = ?CMВ (за першою ознакою рівності трикутників, тоді BC = AD).

Оскільки для трикутника ABD справедливо, що AB + AD > BD або AB + AD > 2ВМ. Враховуючи, що AD = ВС, маємо: AB + ВС > 2ВМ.

Вправи для повторення

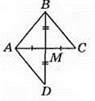
421. Нехай BD = 3х, тоді DC = 7х, AB = 5х.

За умовою CD – BD = 16 см, тоді 7х – 3х = 16; 4х = 16; х = 4. Отже, BD = 12 см, DC = 28 см, AB = 20 см. M – середина відрізка AB, N – середина відрізка CD, тоді

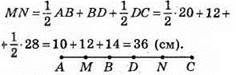
Відповідь: 36 см.

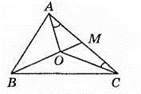
422. ∠OAC = ∠OCA, AM = MC. Оскільки? АОС – рівнобедрений, бо ∠OAC = ∠OCA), то ОМ ⊥ АС. Оскільки ВМ ⊥ AC, ВМ – медіана, то? АВC – рівнобедрений.

Спостерігайте, рисуйте, конструюйте, фантазуйте

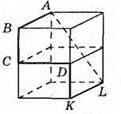
423. Існує шестикутник, жодні дві діагоналі якого не мають спільних точок, відмінних від вершин. Це просторовий шестикутник ABCDKL, який розташований на двох кубах.