Головна ⇒ 📌ГДЗ з математики ⇒ Вертикальні кути. Кут між двома прямими, що перетинаються

Вертикальні кути. Кут між двома прямими, що перетинаються

Розділ 2. Взаємне розміщення прямих па площині

§ 6. Вертикальні кути. Кут між двома прямими, що перетинаються

107. 1) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 15°, дорівнює 15°.

2) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 129°, дорівнює 129°.

Відповідь: 1) 15°; 2) 129°.

108. 1) За властивістю вертикальні кути рівні. Отже, кут, вертикальний до кута 42°, дорівнює 42°.

2) За властивістю вертикальні кути рівні. Отже, кут, вертикальний

до кута 139°, дорівнює 139°.

109. На рис. 65 пари вертикальних кутів – це: ∠BPC і ∠KPL, ∠APB і ∠LPM, ∠APC і ∠KPM, ∠APK і ∠CPM, ∠BPK і ∠LPC, ∠APL і ∠MPB.

110. При перетині двох прямих утворилося чотири кути. Нехай ∠KPN = 40°, тоді ∠LPM = 40°, бо за властивістю вертикальні кути рівні. ∠KPL та ∠LPM – суміжні.

Вертикальні кути. Кут між двома прямими, що перетинаються

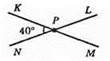
Тоді за властивістю суміжних кутів ∠KPL + ∠LPM = 180°, звідси ∠KPL = 180°- ∠LPM; ∠KPL = 180° -40° = 140°. ∠KPL і ∠NPM – вертикальні. За властивістю вертикальні кути рівні, отже, ∠NPM =140°.

Відповідь: 40°, 140°, 140°.

111. ∠AML та ∠PMB – вертикальні кути. ∠PMB = ∠AML = 120°.

∠AML

та ∠LMB – суміжні, отже, їх сума дорівнює 180°. ∠AML + ∠LMB = 180°, звідси ∠LMB = 180° – ∠AML; ∠LMB = 180° – 120° = 60°.

∠AMP та ∠LMB – вертикальні. ∠AMP = ∠LMB = 60°.

Відповідь: 60°, 120°, 60°.

113. За означенням кутом між прямими, що перетинаються, є менший з кутів, що утворилися при перетині цих прямих. Отже, кутом між прямими AB і PL є кут РОА або кут BOL. ∠POA – суміжний кут до кута РОВ. Отже, ∠POA + ∠POB = 180°, ∠POА = 180° – ∠POB, ∠POA = 180° – 118° = 62°.

Відповідь: 62°.

114.

Вертикальні кути. Кут між двома прямими, що перетинаються

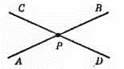
CD і AB – прямі, що перетинаються. Оскільки кут між прямими не може бути більше за 90°, то кутом між прямими CD і AB буде кут АРС або кут BPD. ∠APC = 55°.

Відповідь: 55°.

115.

Вертикальні кути. Кут між двома прямими, що перетинаються

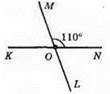
∠MON та ∠KOL – вертикальні, ∠МОК та ∠NOL – вертикальні.

За властивістю вертикальні кути рівні, отже, ∠KOL = ∠MON = 110°.

∠МОК та ∠MON – суміжні, отже, ∠MOK + ∠MON = 180°, звідси ∠MOK = 180° – ∠MON = 180° – 110° = 70°. ∠NOL = ∠MOK = 70°.

Відповідь: 70°, 70°, 110°.

116.

Вертикальні кути. Кут між двома прямими, що перетинаються

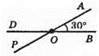
Оскільки OD доповняльний промінь до OB, OP доповняльний промінь до ОА, то ∠АОВ та ∠DOP, ∠DOA та ∠РОВ – вертикальні. За властивістю вертикальні кути рівні. Отже, ∠DOP = ∠АОВ = 30°.∠DOA та ∠АОВ – суміжні. За властивістю суміжних кутів ∠DOA + ∠АОВ = 180°, ∠DOA + 30° = 180°, ∠DOA = 150°. ∠РОВ = ∠DOA = 150°.

Відповідь: 30°, 150°, 150°.

117. 1) Оскільки всі кути рівні між собою, то позначимо градусну міру кожного х. Розглянемо пару суміжних кутів. За властивістю суміжних кутів їх сума дорівнює 180°. х + х = 180°; 2х = 180°; х = 90°. Отже, кожен кут дорівнює 90°. Відповідь: всі кути по 90°.

2) При перетині двох прямих утворюються дві пари вертикальних кутів і чотири пари суміжних. Сума двох будь-яких суміжних кутів дорівнює 180°. За умовою задачі сума кутів дорівнює 178°, отже, ці кути вертикальні.

Один з кутів дорівнює 178° : 2 = 89°, а суміжний з них кут дорівнює 180° – 89° = 91°. Отже, утворилися кути 89°, 89°, 91°, 91°.

Відповідь: 89°, 89°, 91°, 91°.

118. 1) При перетині двох прямих утворюються дві пари вертикальних кутів і чотири пари суміжних. Оскільки сума суміжних кутів дорівнює 180°, а за умовою сума двох кутів дорівнює 16°, то ці кути – вертикальні.

Один з кутів дорівнює 16° : 2 = 8°, а суміжний з ним кут дорівнює 180° – 8° = 172°.

Отже, утворилися кути: 8°, 8°, 172°, 172°.

Відповідь: 8°, 8°, 172°, 172°.

2) Оскільки три з чотирьох кутів рівні, то серед них є пара суміжних кутів, сума яких дорівнює 180°. Позначимо градусну міру кутів х. Тоді х + х = 180°; 2х = 180°; x = 90°. Отже, три з утворених кутів дорівнюють 90°. Тоді і четвертий кут теж 90°, тому що він вертикальний з одним із трьох знайдених кутів. Відповідь: всі кути по 90°.

119. 1) При перетині двох прямих утворюються дві пари вертикальних кутів і чотири пари суміжних кутів. Різниця двох вертикальних кутів дорівнює 0°, а різниця двох суміжних кутів (відмінних від прямих) відмінна від 0°. Отже, за умовою задачі задана різниця двох суміжних кутів.

Менший кут дорівнює (180° – 18°) : 2 = 81°, тоді більший кут дорівнює 180° – 81° = 99°. За означенням, якщо кутом між прямими, що перетинаються, є менший з кутів, то цей кут дорівнює 81°.

Відповідь: 81°.

2)

Вертикальні кути. Кут між двома прямими, що перетинаються

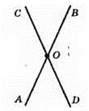
Нехай за умовою ∠СОА + ∠AOD + ∠DOB = 293°. ∠СОА і ∠AOD – суміжні, тому ∠СОА + ∠AOD = 180°. Отже, кут DOB = 293° – 180° = 113°.

∠СОВ і ∠DOB – суміжні, отже, їхня сума 180°. ∠СОВ + 113° = 180°; ∠СОВ = 180° – 113° = 67°. ∠СОВ – кут між прямими, що перетинаються.

Відповідь: 67°.

120. Оскільки вертикальні кути рівні, то за умовою задачі задані суміжні кути. Нехай градусна міра меншого кута дорівнює х, тоді більшого – 2х. За властивістю суміжних кутів їхня сума дорівнює 180°. Отже, маємо х + 2х= 180°; 8х = 180°; х = 60°. Тож кут між прямими дорівнює 60°.

Відповідь: 60°.

121.

Вертикальні кути. Кут між двома прямими, що перетинаються

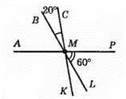
∠BMC = ∠KML = 20° (як вертикальні кути). ∠KMP = ∠KML + ∠LMP – 20° + 60° = 80° (згідно з основною властивістю вимірювання кутів).

∠AMK і ∠KMP – суміжні. ∠AMK + ∠KMP = 180°, ∠AMK + 80° = 180°. ∠AMK = 180° – 80° = 100°.

Відповідь: 100°.

122.

Вертикальні кути. Кут між двома прямими, що перетинаються

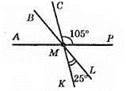
∠BMC = ∠KML = 25° (як вертикальні кути). ∠BMP = ∠BMC + ∠CMP = 25° + 105° = 130° (згідно з основною властивістю вимірювання кутів). ∠AMB і ∠BMP – суміжні. ∠AMB + ∠BMP = 180°, ∠AMB + 130° = 180°, ∠AMB = 180° – 130° = 50°.

Відповідь: 50°.

123.

Вертикальні кути. Кут між двома прямими, що перетинаються

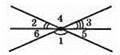
Кути 2, 4 і 3 утворюють розгорнутий кут, отже ∠2 + ∠4 + ∠3 = 180°.

∠1 = ∠4 – як вертикальні кути. Звідси ∠1 + ∠2 + ∠3 = 180°.

Відповідь: 180°.

124.

Вертикальні кути. Кут між двома прямими, що перетинаються

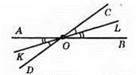
Нехай ∠COB і ∠AOD – вертикальні, ОL – бісектриса кута СОВ, ОК – бісектриса кута AOD. Доведемо, що ∠KOL = 180°. Оскільки ∠COB = ∠AOD, то ∠BOL = ∠AOK – як половини рівних кутів.

Тоді ∠KOL = ∠AOK + ∠AOC + ∠COL = ∠AOC + (∠BOL + ∠COL) = ∠AOC + ∠COB = 180°. Отже, бісектриси вертикальних кутів утворюють розгорнутий кут. Отже, OL доповняльний до ОК.

125. Десять точок на прямій розбивають відстань між крайніми точками на 9 відрізків по 2 см кожний. Отже, відстань між крайніми точками дорівнює 9 x 2 = 18 (см).

Відповідь: 18 см.

126. 1) Ні; 2) так; 3) ні; 4) ні; 5) так; 6) ні.

127. 1) 14; 2) Вертикальні кути. Кут між двома прямими, що перетинаються

Домашня самостійна робота № 1 (§§ 1-6)

1. Як прямій а, так і прямій b належить точка М. Отже, відповідь В) М.

2. Оскільки тупий кут більший за прямий, але менший від розгорнутого, то правильна відповідь A) ∠M = 129°.

3. Оскільки сума суміжних кутів дорівнює 180°, то правильна відповідь Б) 27° і 153°.

4.

Вертикальні кути. Кут між двома прямими, що перетинаються

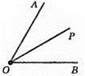
Згідно з основною властивістю вимірювання кутів маємо: ∠AOB = ∠AOP + ∠POB = 20° + 50° = 70°. Отже, правильна відповідь Б) 70°.

5. Вертикальні кути. Кут між двома прямими, що перетинаються

Згідно з основною властивістю вимірювання відрізків AL + LB = AB, звідси AL = АВ – LB = 8 см – 5 см = 3 см. Отже, правильна відповідь Г) 3 см.

6. При перетині двох прямих утворюються дві пари вертикальних кутів і чотири пари суміжних кутів. Оскільки сума суміжних кутів дорівнює 180°, а за умовою сума двох кутів дорівнює 160°, то ці кути вертикальні. Один з них дорівнює 160° : 2 = 80°, а суміжний з ним кут дорівнює 180°-80°= 100°.

За означенням, якщо кутом між прямими, що перетинаються, є менший з кутів, то цей кут дорівнює 80°. Отже, правильна відповідь В) 80°.

7. Вертикальні кути. Кут між двома прямими, що перетинаються

Оскільки ВС = AB + АС, 7 см = 4 см+ 3 см, 7 см = 7 см, то точка А лежить між точками В і С. Отже, правильна відповідь А).

8. ∠COK = ∠KOB = 35° (оскільки ОК – бісектриса кута СОВ), ∠AOB – розгорнутий, ∠AOB = 180°, ∠AOB = ∠AOK + ∠KOB, 180° = ∠AOK + 35°, ∠AOK = 180° -35° = 145°. Отже, правильна відповідь В) 145°.

9. Нехай один із суміжних кутів х, тоді другий 2х. Оскільки сума суміжних кутів дорівнює 180°, маємо: х + 2х = 180°; 3х = 180°; х = 60°; 2х = 120°. Отже, правильна відповідь Г) 120°.

10.

Вертикальні кути. Кут між двома прямими, що перетинаються

Правильна відповідь Г) 120°.

11.

Вертикальні кути. Кут між двома прямими, що перетинаються

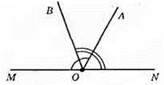
∠AON = ∠MON – ∠MOA = 180° – 120° = 60°. ∠MOB = ∠MON – ∠NOB = 180° – 110° = 70°. ∠BOA = ∠MON – ∠AON – ∠MOB = 180° – 60° – 70° = 50°. Отже, правильна відповідь А) 50°.

12. Нехай градусна міра одного з кутів х, тоді другого 2х. Кут, суміжний з першим кутом – 180° – х, з другим – 180° – 2х. 3а умовою 180° – х – (180° – 2х) = 70°; 180° – х – 180° + 2х = 70°; х = 70°; 2х = 140°. Отже, правильна відповідь Г) 140°.

Завдання для перевірки знань (§§ 1-6)

1. В є a, D є а, М ∉ а, С ∉ а.

2. 1) ∠A = 92° – тупий;

2) ∠B = 180° – розгорнутий;

3) ∠C = 90° – прямий;

4) ∠D = 31° – гострий.

3. ∠BAD і ∠KAN, ∠BAK і ∠DAN – вертикальні.

4. Вертикальні кути. Кут між двома прямими, що перетинаються

MN = CM + CN, звідси CM = MN – CN = 7,2 см – 3,4 CM = 3,8 CM.

Відповідь: 3,8 см.

5.

Вертикальні кути. Кут між двома прямими, що перетинаються

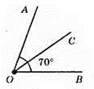
∠AOB = 70°, ОС – бісектриса кута АОВ.

6.

Вертикальні кути. Кут між двома прямими, що перетинаються

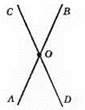
∠AOC i ∠COB – суміжні. ∠AOC + ∠COB = 180°, ∠COB = 180° – 132° = 48°. ∠COB – кут між прямими AB і CD.

Відповідь: 48°.

7. Вертикальні кути. Кут між двома прямими, що перетинаються

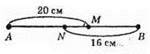
AN – AB – BN = 30 – 16 = 14 (CM), MB = AВ – AM = 30 – 20 = 10 (CM), MN = AB – (AN + MB) = 30 – (14 + 10) = 30 – 24 = 6 (CM).

Відповідь: 6 CM.

8.

Вертикальні кути. Кут між двома прямими, що перетинаються

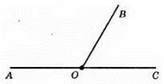
Нехай градусна міра кута ВОС – x, тоді ∠AOВ = х + 12.

Оскільки сума суміжних кутів дорівнює 180°, маємо: х + х + 12° = 180°; 2x = 168°; x = 84°. Отже, один з кутів дорівнює 84°, тоді другий – 84° + 12° = 96°.

Відповідь: 84°, 96°.

9. Задача має два розв’язки.

I розв’язок: Вертикальні кути. Кут між двома прямими, що перетинаються

AВ = АК + КВ = 9,3 + 3,7 = 13 (см).

II розв’язок: Вертикальні кути. Кут між двома прямими, що перетинаються

AВ = АК – КВ = 9,3 – 3,7 = 5,6 (см).

Додаткові вправи

10.

Вертикальні кути. Кут між двома прямими, що перетинаються

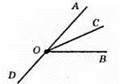
∠АОВ = 48°, ОС – бісектриса кута АОВ.

∠АОС = ∠СОВ = 48° : 2 = 24° (оскільки ОС – бісектриса кута АОВ). OD – доповняльний промінь до сторони ОА кута АОС. ∠AOD = 48°. ∠AOD = ∠AOC + ∠COD, звідси ∠COD = ∠AOD – ∠AOC = 180° – 24° = 156°.

Відповідь: 156°.

11. Нехай один з кутів х, тоді другий – 3х.

Кут, суміжний з першим кутом – 180° – х, а другим – 180° – 3х. Градусні міри цих кутів відносяться, як 7 : 3. Складемо пропорцію: 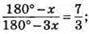Вертикальні кути. Кут між двома прямими, що перетинаються 3(180° – х) = 7(180° – 3х); 540 – 3х = 1260 – 21х; 18х = 720°; х = 40°. Отже, один з кутів дорівнює 40°, другий – 40° х 3 = 120°.

Відповідь: 40°, 120°.


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Вертикальні кути Розділ 1. Найпростіші геометричні фігури та їх властивості § 5. Вертикальні кути 152. 1) ∠AYX і ∠BYZ – вертикальні; 2) ∠OLK і ∠MLN – не вертикальні. 153. 1) ∠AOD – вертикальний з кутом 1; 2) ∠АОС і ∠DOB – суміжні з кутом 1. 154. ∠BOA і ∠COD – суміжні. ∠BOA = ∠COD = 60°. 155. […]...

  2. Суміжні та вертикальні кути § 1. Найпростіші геометричні фігури та їхні властивості § 4. Суміжні та вертикальні кути Практичні завдання 86. ∠BAC – гострий, ∠OAB – суміжний до кута ВАС. ∠АОВ – прямий, ∠COA – суміжний до кута АОВ. ∠BOC – тупий, ∠AOB – суміжний до кута ВОС. 87. ∠AOC і ∠COB – суміжні. 88. а) ∠ABD i ∠CBD; […]...

  3. Вертикальні кути. Кут між прямими Урок № 11 Тема. Вертикальні кути. Кут між прямими Мета: домогтися засвоєння учнями означення вертикальних кутів, формулювання і доведення теореми про властивість вертикальних кутів; означення кутів між прямими. Сформувати вміння: – будувати вертикальні кути; – знаходити вертикальні кути на рисунку; – розв’язувати задачі із застосуванням теореми про рівність вертикальних кутів та суму суміжних кутів. Тип […]...

  4. Суміжні й вертикальні кути Геометрія Основні властивості найпростіших геометричних фігур Суміжні й вертикальні кути Два кути називаються Суміжними, якщо в них одна сторона спільна, а інші сторони є доповняльними півпрямими. На рисунку і – суміжні. Властивості суміжних кутів Теорема 1. Сума суміжних кутів дорівнює . (Зверніть увагу: кути, сума яких дорівнює , не обов’язково суміжні.) Теорема 2. Коли два […]...

  5. Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих Розділ 2. Взаємне розміщення прямих па площині § 9. Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих 170. Рис. 119: ∠1 і ∠2 – внутрішні різносторонні кути. Рис. 120: ∠1 і ∠2 – відповідні кути. Рис,121: ∠1 i ∠2 – внутрішні різносторонні кути. 171. Внутрішні односторонні кути: ∠ANM і ∠NMB, ∠CNM і ∠NMD. […]...

  6. СУМІЖНІ І ВЕРТИКАЛЬНІ КУТИ Геометрія Евкліда є лише першим кроком до вивчення форм реального простору. О. Смогоржевський РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ У цьому розділі підручника ви розширите і поглибите свої знання про прямі і промені однієї площини, ознайомитеся з дуже важливими поняттями: суміжні кути, вертикальні кути, перпендикулярні прямі, паралельні прямі тощо, а також із важливими загальноматематичними […]...

  7. Вправи для повторення до розділу 2 Розділ 2. Взаємне розміщення прямих па площині Вправи для повторення до розділу 2 До § 5. 226. На рис. 184 суміжні кути ∠2 і ∠3. на рис. 185 суміжні кути ∠1 і ∠4 та ∠2 i ∠3. На рис. 186 суміжні кути ∠1 і ∠2 та ∠3 i ∠4. 227. 1) Так, можна. Треба побудувати […]...

  8. Многогранні кути 607. Правильний октаедр має 8 граней, кожна з яких – правильний трикутник. Він має 6 чотиригранних кутів. 608. Чотиригранний кут 40°; 70°; 110° і 140° існує неопуклий. 609. Якщо всі плоскі кути чотиригранного кута рівні, то кожний його двогранний кут дорівнює протилежному (октаедр). Площини, які проходять через його протилежні ребра, – перпендикулярні. 611. Якщо у […]...

  9. Зовнішній кут трикутника та його властивості Розділ 3. Трикутники. Ознаки рівності трикутників § 18. Зовнішній кут трикутника та його властивості 438. ∠BAK – зовнішній кут при вершині А. 439. ∠LDP – зовнішній кут при вершині D. 441. ∠A + ∠B = 70° – за властивістю зовнішнього кута трикутника. 442. Зовнішній кут трикутника при вершині С дорівнює 74° згідно з властивістю зовнішнього […]...

  10. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої Розділ 2. Взаємне розміщення прямих па площині § 7. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої 128. m ⊥ n, MN ⊥ АВ. 129. KA ⊥ c, ВМ ⊥ с. 130. ВL ⊥ a. MВ ⊥ a. 131. 1) Відрізки AB і MN перпендикулярні, оскільки вони лежать на перпендикулярних прямих a і b. 2) […]...

  11. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 19. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників 466. 1) PF – гіпотенуза, PL і LF – катети. 2) PF довша за PL, PF довша за LF, оскільки PF – гіпотенуза. 467. На рис. 321 трикутники рівні за двома катетами. Оскільки АС = ML, СВ = LP, […]...

  12. Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною Розділ 2. Взаємне розміщення прямих па площині § 10. Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною 199. 1) ∠1 = ∠8, ∠6 = ∠3 (як відповідні кути при паралельних прямих а і b і січній с). 2) ∠2 = ∠4 (як внутрішні різносторонні кути при паралельних прямих а і b і […]...

  13. Кут. Вимірювання кутів. Бісектриса кута Розділ 1. Елементарні геометричні фігури та їхні властивості § 3. Кут. Вимірювання кутів. Бісектриса кута 33. 1) М – вершина кута, МА і МК – сторони кута АМК; 2) L – вершина кута, LP і LF – сторони кута PLF; 3) N – вершина кута, NB i NC – сторони кута BNC. 34. 1) O […]...

  14. Вправи 150-175 150. ∠1 = 90°, ∠2 = ∠1 = 90° – вертикальні кути; ∠3 – суміжний куту ∠1. ∠3 = 180° – 90° = 90°, ∠3 = ∠4 = 90° (вертикальні кути). 151. ∠(ac) = 70°; ∠(ab) = 90°; ∠(bc) = 90° – ∠(ac) = 90° – 70° = 20°. 152. а ⊥ с; ∠(ab) = […]...

  15. Властивості кутів трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 10. Властивості кутів трикутника 344. ∠E = 60°, ∠F = 40°, ∠D = 80°. ∠E + ∠F + ∠D = 60° + 40° + 80° = 180°. 345. На мал. 208 неправильно сказано градусну міру кутів? АВС, оскільки? ABC – прямокутний, a ∠B + ∠C = […]...

  16. Тригранний і многогранний кути Геометрія Многогранники Тригранний і многогранний кути Нехай промені a, b, c виходять з однієї точки й не лежать в одній площині. Тригранним кутом називається фігура, яка складається з трьох плоских кутів , , (див. рисунок). Ці кути називаються Гранями тригранного кута, а їх сторони – Ребрами. Спільна вершина плоских кутів називається Вершиною тригранного кута. Двогранні […]...

  17. Властивості й ознака рівнобедреного трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 12. Властивості й ознака рівнобедреного трикутника 476. На мал. 72: ML і МК – бічні сторони, KL – основа, ∠K = ∠L. 477. KD = DF, КЕ = EF, ∠K = ∠F, ∠KDE = ∠FDE, ∠DEK = ∠DEF = 90°. 478. Щоб провести бісектрису, медіану і […]...

  18. Суміжні кути Урок № 10 Тема. Суміжні кути Мета: домогтися розуміння учнями змісту наслідків з теореми про суму суміжних кутів та змісту понять “наслідок”, “посилання”; використовуючи знання теореми про суміжні кути та її наслідки, виробити вміння розв’язувати задачі на обчислення та доведення, в яких йдеться про суміжні кути. Тип уроку: застосування знань, умінь та навичок. Наочність і […]...

  19. Вправи 375-424 375. ВС – бісектриса ∠ABD; ∠ABD = 80° + 80° = 160°; ∠BAC + ∠ABD = 20° + 160° = 180°; ∠BAC і ∠ABD – внутрішні односторонні кути при прямих АС і BD та січній АВ. Отже, BD || АС. 376. ∠A = 70°, ∠B = 40°, BE – бісектриса ∠ABD; ∠DBE = ∠ABE = […]...

  20. Сума кутів трикутника Геометрія Основні властивості найпростіших геометричних фігур Сума кутів трикутника Теорема. Сума кутів трикутника дорівнює . Із цієї теореми випливають наслідки: 1. У будь-якому трикутнику принаймні два кути гострі (тобто в трикутнику не може бути більше одного прямого або тупого ­кута). 2. Кути рівностороннього трикутника дорівнюють . Зовнішнім кутом трикутника при даній вершині називається кут, суміжний […]...

  21. Тригранні кути 562. Нехай дано тригранний кут, усі плоскі кути якого прямі. Лінійний кут кожного тригранного кута прямий, отже всі його двогранні кути прямі. 563. Якщо всі двогранні кути тригранного кута рівні, то кожний з них більше за 60°, оскільки ∠1 + ∠2 + ∠3 > 180°; ∠Α = ∠1 – ∠2 = ∠3, то 3∠A > […]...

  22. Кути трикутника і чотирикутника Урок № 50 Тема: Кути трикутника і чотирикутника Мета. Познайомити учнів з видами кутів і трикутників в залежності від кутів, які входять до кута. Навчити учнів вимірювати кути за допомогою транспортира. Формувати уміння і навички розв’язувати геометричні задачі. Розвивати логічне мислення учнів, шляхом розв’язування задач, продовжувати формувати вміння працювати з підручником. Форми роботи: бліцопитування, робота […]...

  23. Кут між мимобіжними прямими Геометрія Стереометрія Кут між мимобіжними прямими Дві прямі, що перетинаються, утворюють суміжні та вертикальні кути. Кутова міра меншого із суміжних кутів називається Кутом між прямими. Кут між перпендикулярними прямими дорівнює за означенням. Кут між паралельними прямими вважаємо таким, що дорівнює нулю. Кутом між мимобіжними прямими називається кут між прямими, які перетинаються й паралельні даним мимобіжним […]...

  24. Кути та їх міри Урок № 18. Тема. Кути та їх міри Мета. Засвоїти поняття кута градусної міри кута, променя, що проходить між сторонами кута; вимірювати кути; записувати кути з малюнка; застосовувати властивості кутів до розв’язання задач, розвивати увагу та допитливість, виховувати інтерес до математики. Обладнання: кодоскоп Хід уроку І. Організація класу ІІ. Перевірка домашнього завдання. Двоє учнів розв’язують […]...

  25. Відрізок. Вимірювання відрізків. Відстань між двома точками Розділ 1. Елементарні геометричні фігури та їхні властивості § 2. Відрізок. Вимірювання відрізків. Відстань між двома точками 13. На рисунку зображені відрізки: AB, AK, BK, ВМ. AK = 38 мм, MB = 12 мм. 14. На рисунку зображені відрізки: PC, PD, CD, PT. PC = 9 мм. PD = 31 MM. PT = 27 мм. […]...

  26. Ознаки паралельності двох прямих § 3. Паралельні прямі. Сума кутів трикутника 13. Ознаки паралельності двох прямих Практичні завдання 300. 1) Кути АОМ і CEO – відповідні; 2) кути АОЕ і СЕК – відповідні; 3) кути АОE і OED – різносторонні; 4) кути АОЕ і CEO – односторонні. 1) відповідні; 2) односторонні; 3) різносторонні. 301. 1) ∠1 i ∠5; ∠2 […]...

  27. Вправи 100-49 100. А || b, с || d. 4 точки перетину. 101. 1) Всі чотири прямі перетинають пряму с. 2) Одна пряма паралельна, три перетинають пряму с. 102. 1) m || с; 2) m || b; в) m || а. 103. а || b. Якщо b i c не перетинаються, то через т. М проведено 2 […]...

  28. Кути та їх вимірювання Урок № 19 Тема. Кути та їх вимірювання Мета. Формувати уміння та навички будувати кут заданої величини, порівнювати кути, визначати їх градусну міру, користуючись транспортиром, розрізняти на око прямий, тупий та гострий кути. Розвивати окомір, виховувати охайність та старанність. Хід уроку I. Організація класу. II. Перевірка домашнього завдання. 1. Фронтальне опитування А) Що називають кутом? […]...

  29. Рівняння. Кути. Прямокутник. Трикутник і його види УРОК 41 Тема. Рівняння. Кути. Прямокутник. Трикутник і його види Мета: підготовити учнів до тематичної контрольної роботи. Тип уроку: повторення і систематизація знань. Хід уроку I. Актуалізація опорних знань Усні вправи 1. Знайти корінь рівняння: 1) х + 15 = 29; 2) 30 – х = 17; 3) х – 12 = 19; 4) 12 […]...

  30. Рівняння. Кути. Трикутники УРОК 42 Тема. Рівняння. Кути. Трикутники Мета: перевірити рівень засвоєння учнями навчального матеріалу; перевірити рівень сформованості вмінь учнів: вимірювати і будувати кути за допомогою транспортира; обчислювати невідомі сторони й периметр трикутника; розв’язувати рівняння з використанням правил знаходження невідомих компонентів дій додавання і, віднімання. Тип уроку: контроль знань. Хід уроку І. Тематична контрольна робота № 3 […]...

  31. Промінь. Кут. Вимірювання кутів § 1. Найпростіші геометричні фігури та їхні властивості 3. Промінь. Кут. Вимірювання кутів Практичні завдання 49. Промені AB і АС – не доповняльні. Промінь AN – доповняльний до променя AB, а промінь AM – доповняльний до променя АС. На рисунку зображено промені АB, АС, AN, AM. 50. Промені AB і ВА не е доповняльними, оскільки […]...

  32. Рівнобедрений трикутник і його властивості § 2. Трикутники 8. Рівнобедрений трикутник і його властивості Практичні завдання 196. 197. 198. Вправи 199. 1) Р = 13 + 2 х 8 = 29(см). Відповідь: 29 см. 2) Нехай х см – бічна сторона, тоді 15 + 2х = 39, тоді 2х = 39 – 15; 2х = 24; х = 24 : […]...

  33. Перша та друга ознаки рівності трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 13. Перша та друга ознаки рівності трикутників 301. На рис. 227 трикутники рівні за першою ознакою (за двома сторонами і кутом між ними). На рис. 228 трикутники рівні за другою ознакою (за стороною і прилеглими двома кутами). 302. У? ABC і? CDA спільний елемент – сторона AВ. У? […]...

  34. Кути трикутника і чотирикутника. Розв’язання задач Урок № 51 Тема. Кути трикутника і чотирикутника. Розв’язання задач Мета. Продовжити формування в учнів. вміння розв’язувати задачі геометричного змісту, повторити основні поняття теми, сприяти формуванню практичних навичок при виконанні вправ. Форми роботи: фронтальна бесіда, індивідуальна робота біля дошки, виконання тренувальних вправ, робота з підручником. Обладнання: лінійка, транспортир, кольорова крейда, косинець, таблиці. Тип уроку: урок […]...

  35. Описане та вписане коло трикутника § 3. Паралельні прямі. Сума кутів трикутника § 20. Описане та вписане коло трикутника 540. 1) Різносторонній гострокутний трикутник. 2) Прямокутний трикутник. 3) Тупокутний трикутник. 541. 1) Рівнобедрений гострокутний трикутник. 2) Рівнобедрений тупокутний трикутник. 542. 543. 544. Вправи 545. Медіана BD рівнобедреного трикутника ABC є в той же час і серединним перпендикуляром до сторони АС […]...

  36. Рівність геометричних фігур Розділ 1. Найпростіші геометричні фігури та їх властивості § 11. Рівність геометричних фігур 397. Щоб сумістити фігури F1 i F, можна скопіювати фігуру F1 на кальку, потім перевернути кальку і покласти на фігуру F. 398. Відрізки OP і MN сумістити не можна, бо вони мають різну довжину. 399. Кути ABC і MON сумістити не можна, […]...

  37. Двогранні кути 520. Нехай дано двогранний кут, міра якого 60°, ∠AOB = 60°. AO + MN, BO + MN, АВ + β, АВ = 12 см. ΔАОВ – прямокутний. 521. Нехай дано двогранний кут, який дорівнює 45°. т. В? α, ОВ = 8 дм. АВ + β. Δ ΟΒΑ – прямокутний. 522. Нехай дано двогранний кут ∠BOA. […]...

  38. Дотична до кола, її властивості Розділ 4. Коло і круг. Геометричні побудови § 22. Дотична до кола, її властивості 607. Проведемо радіус ОР, а потім за допомогою косинця побудуємо пряму m, перпендикулярну до радіуса. За теоремою 2 пряма m є дотичною до кола. 608. Проведемо радіус ОМ, а потім за допомогою косинця побудуємо пряму n, перпендикулярну до радіуса. За теоремою […]...

  39. Властивості прямокутного трикутника § 3. Паралельні прямі. Сума кутів трикутника § 17. Властивості прямокутного трикутника 457. Найбільший катет трикутника дорівнює 24 см. 458. ?DEF – прямокутний, ∠F = 90°, ∠D = 30°, DE = 18 см. Відповідь: 9 см. 459. ?KCM – прямокутний, ∠M = 90°, ∠C = 60°, MC = 7 см. ∠MKC = 90° – 60° […]...

  40. Кут між мимобіжними прямими Урок 53 Тема. Кут між мимобіжними прямими Мета уроку: формування поняття кута між мимобіжними прямими, а також вмінь учнів знаходити кути між мимобіжними прямими. Обладнання: стереометричний набір, моделі куба, тетраедра, прямокутного паралелепіпеда. Хід уроку II. Перевірка домашнього завдання В кінці уроку збираються учнівські зошити для перевірки їх ведення і виконання домашнього завдання. III. Сприйняття й […]...

Ви зараз читаєте: Вертикальні кути. Кут між двома прямими, що перетинаються
«
»