Властивості модуля – Модуль і його властивості
Математика – Алгебра
Модуль і його властивості
Модуль числа – це відстань від 0 до точки, що відповідає цьому числу на координатній прямій, виміряна в одиничних відрізках.
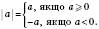
Отже, 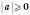 для всіх значень a.
для всіх значень a.
Властивості модуля
1. 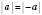 .
.
2. Якщо 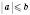 , то
, то 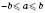 .
.
3. Якщо 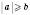 , то
, то 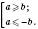
4. Модуль суми скінченного числа дійсних чисел не перевищує суми модулів
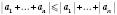 .
.5. Модуль різниці не менший за різницю модулів цих чисел:
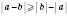 .
.6. Модуль добутку скінченного числа співмножників
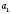 , …,
, …, 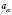 дорівнює добутку модулів цих співмножників:
дорівнює добутку модулів цих співмножників: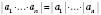 .
.7. Модуль частки дорівнює частці від ділення модуля діленого на модуль дільника:
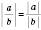 , якщо
, якщо 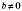 .
.Приклади розв’язування рівнянь та нерівностей, що містять знак модуля
1)
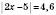
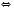
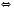
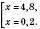
Відповідь:
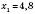 ,
, 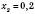 .
.2)
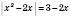
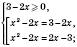
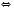
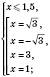
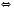
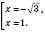
Треба враховувати, що модуль будь-якого числа є числом невід’ємним, отже, корені
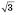 і 3 є сторонніми.
і 3 є сторонніми.Відповідь:
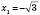 ,
, 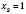 .
.3)
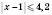
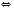
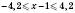
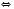
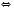
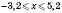 .
.Відповідь:
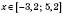 .
.4)
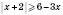
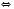
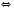
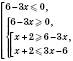
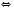
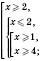
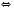
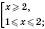
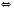
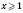 .
.Відповідь:
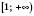 .
.Складаючи першу сукупність, ми урахували, що модуль будь-якого числа є завжди число невід’ємне. Із цього випливає, що при тих значеннях x, коли права частина є числом недодатним, нерівність завжди виконується.
5) Дуже корисним у розв’язуванні завдань з модулем є спосіб поділення координатної прямої на такі інтервали, що в них можна визначити знак підмодульного виразу й розкрити знак модуля.
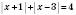 .
.Знайдемо, при яких значеннях х підмодульні вирази перетворюються на нуль:
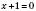 ;
; 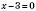 ;
;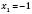 .
. 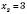 .
.Отже, розіб’ємо числову пряму на три інтервали й будемо розв’язувати рівняння на кожному з них окремо (див. рисунок).
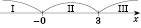
Щоб визначити, який знак має на певному інтервалі кожний із підмодульних виразів, досить підставити в нього замість х довільне число з цього інтервалу.
І.
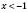 .
.Візьмемо, наприклад,
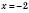 , тоді
, тоді,
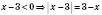 .
.Отже, маємо:
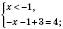
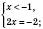
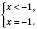 На цьому інтервалі розв’язків не має.
На цьому інтервалі розв’язків не має.  .
.ІI.
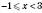 .
.Беремо
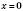 ,
, 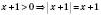 ;
;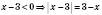 .
.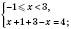
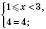
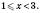
III.
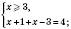
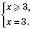
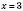 .
.Об’єднуємо розв’язки, отримані на всіх трьох інтервалах (I, II і III).
Відповідь:
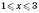 .
.ТУМАН »