Головна ⇒ 📌Плани-конспекти уроків по математиці ⇒ Властивості степеня з натуральним показником (продовження). Степінь степеня

Властивості степеня з натуральним показником (продовження). Степінь степеня

Урок № 23

Тема. Властивості степеня з натуральним показником (продовження). Степінь степеня

Мета: свідоме засвоїти зміст властивостей піднесення степеня до степеня, виробляти вміння виконувати перетворення виразів із застосуванням раніше набутих знань про властивості степеня в комплексі з названою властивістю; систематизувати знання учнів про властивості степеня.

Тип уроку: засвоєння знань, умінь та навичок.

Хід уроку

I. Перевірка домашнього завдання

@ Серед вправ, запропонованих учням для виконання вдома, на особливу

увагу заслуговують: № 1 (8, 9), № 2. Тому їх перевіримо (біля дошки працюють два учні). Усі інші учні самостійно виконують завдання бліц-контролю.

№ 1. Які з рівностей правильні:

1) 514 : 57 = 12;

2) 514 : 57 = 52;

3) 514 : 57 = 17;

4) 514 : 57 = 57?

№ 2. Запишіть у вигляді степеня з основою х.

1) х5 : х3;

2) х4 : х;

3) х5 : хn (n? 5);

4) х2n-1 : хn.

№ 3. Обчисліть 16 : (22 – 23).

@ Під час перевірки виконаних вправ бліц-контролю, повторюємо вивчену напередодні властивість частки степенів з однаковою основою та основну властивість степеня.

II. Робота з випереджальним домашнім завданням

@ На дошці записано умову домашнього завдання

(див. № 3 домашнього завдання попереднього уроку) й учні самостійно працюють над заповненням таблиці:

Степінь

Основа степеня

Показник

Запис у вигляді добутку

Спрощений вираз

Запис у вигляді тотожності

Висновки

Корекція

III. Засвоєння знань

@ Основна навчальна мета уроку – не тільки сформулювати відповідну властивість степеня, а й виділити “місце” цієї властивості серед вивчених раніше властивостей степеня. Тобто учні повинні усвідомити не тільки те, що під час піднесення степеня в степінь основа не змінюється, а показники перемножуються, але й той факт, що вивчені властивості дають нам можливість у разі, коли мова йде про добуток або частку, або степінь степеня (для добутку й частки основа повинна бути однаковою), виконувати дії тільки із показниками цих степенів.

Доведення властивості степінь степеня проводимо, спираючись на основну властивість степеня.

Запис у зошитах учнів має такий вигляд:

Конспект 9

Степінь степеня

1. Якщо a – будь-яке, т, п – натуральні числа, то (ат)n = amn.

2. Приклад: 1) (a5)3 = а5 – 3 = а15; 2) .

3) .

IV. Застосування знань. Засвоєння вмінь та навичок

@ Серед вправ, що винесені на опрацювання, виділяємо такі:

1) на закріплення алгоритму піднесення степеня до степеня;

2) на подання степеня у вигляді степеня із заданим показником;

3) вправи, що передбачають комплексне застосування алгоритмів множення та ділення степенів з однаковою основою та піднесення степеня до степеня.

Виконання усних вправ

1. Піднесіть до степеня:

1) (m3)4; 2)(n10)2; 3) (b15)4; 4) (cx)2; 5) (аn+1)3; 6) (xn+2)n.

2. Поставте замість * таке число або букву, щоб запис був правильним (якщо це можливо).

1) (m*)3 = m6; 2) (m5)* = m15; 3) (m3)* = m10; 4) ((*)2)6 = m24.

3. Степенями яких натуральних чисел є числа: 4; 8; 9; 16; 25; 27; 32; 36; 49? Яким чином ви продовжили б цей ряд?

Виконання письмових вправ

1. Подайте у вигляді степеня вираз:

1) (а6)2;

2) (-а5)4;

3) х4 – х3;

4) (х4)3;

5) ((а3)2)5;

6) (a10)3 – (a5)4;

7) (-a6)7 – (-a3)3 : a15;

8) a24 : (a8)2 – a13.

@ Найтиповіші помилки, які слід одразу ж попереджувати, – це плутанина з діями, що їх треба виконувати з показником; по-друге, робота зі знаками (привчаємо учнів до того, що знаки виразів треба визначати в першу чергу), по-третє, стежимо за порядком виконання дій: піднесення до степеня – дія 3-го ступеня, виконується в першу чергу (якщо немає інших); множення і ділення – дії 2-го ступеня, виконуються в другу чергу, причому в порядку, в якому вони записані (якщо читати зліва направо).

2. Обчисліть значення виразу (у разі необхідності використовуємо таблиці степенів натуральних чисел).

1) 218 : (27)2;

2) (78)2 : (73)5;

3) 115 – (113)7 : 1126;

4) 92 – 273;

5) ;

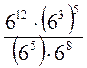6) .

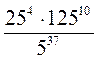@ У прикладі 2.6) звертаємо ще раз увагу на те, що під час множення і ділення степенів за вивченим алгоритмом необхідно, щоб степені мали однакову основу, тому перехід до однієї основи (цей термін треба виділити й акцентувати на ньому) є першим обов’язковим кроком під час розв’язування цих вправ.

3*. Обчисліть значення виразу:

1) 3 – 26 – 8 – 43 + 5 – 82;

2) 4 – 36 – 11 – 272 + 7 – 93.

4*. Подайте у вигляді степеня вираз:

1) (am – a3)n;

2) (bn+2 : b)k;

3) (ak – ak)n;

4) (x2)m – (x3)k.

5*. Подайте z20 У вигляді степеня з основою: z2; z4; z5; z10.

V. Підсумок уроку. Рефлексія

Які з рівностей є неправильними:

1) m5 – m3 = m8;

2) m5 + m3 = m8;

3) (m5)3 = m8;

4) (m5)3 = m15;

5) m5 : m7 = m8;

6) ;

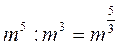7) m5 : m3 = m2;

8) m5 – m3 = m2;

9) m5 – m3 – m2 = 0?

Чому?

VI. Домашнє завдання

№ 1. Подайте у вигляді степеня вираз:

1) (y4)3;

2) (-x6)2;

3) m5m4;

4) (m5)4;

5) ;

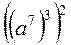6) (a6) – (a2)4;

7) (-a5)3 – (-a4)7 : a12;

8) a32 : (a9)3 – a.

№ 2. Обчисліть значення виразу:

1) 224 : (28)2;

2) (113)4 : (115)3 ;

3) ;

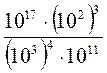4) .

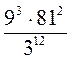№ 3. Випереджальне домашнє завдання. Використовуючи означення степеня з натуральним показником та сполучну властивість множення і користуючись алгоритмом доведення, доведіть, що:

1) (2 – 3)5 = 25 – 35;

2) .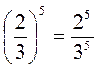
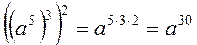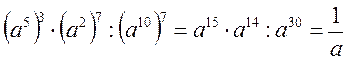