Головна ⇒ 📌ГДЗ з математики ⇒ Вправи 100-49

Вправи 100-49

100.

Вправи 100 49

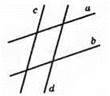
А || b, с || d. 4 точки перетину.

101. 1)

Вправи 100 49

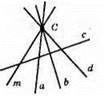
Всі чотири прямі перетинають пряму с.

2)

Вправи 100 49

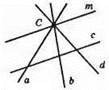
Одна пряма паралельна, три перетинають пряму с.

102.

Вправи 100 49

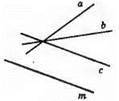
1) m || с; 2) m || b; в) m || а.

103. а || b.

Вправи 100 49

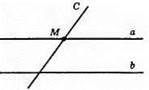
Якщо b i c не перетинаються, то через т. М проведено 2 прямі паралельні b, що неможливо.

104. а і b – перетинаються; с || b, d || а. Прямаdперетинає прямі b i c.

Вправи 100 49

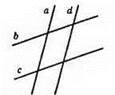
105.

Вправи 100 49

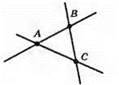
106.

b || с.

Вправи 100 49

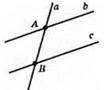
107.

Вправи 100 49

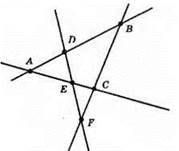
4 прямі перетинаються в 6 точках.

108. 1)

Вправи 100 49

∠(bd) = ∠(ad) – ∠(ac) – ∠(bc);

∠(bd) = 180° – 135° – 20° = 25°;

∠(bd) = 25°;

2)

Вправи 100 49

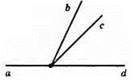
∠(bd) = ∠(bc) + ∠(cd);

∠(cd) = 180° – 135° = 45°;

∠(bd) = 20° + 45° = 65°.

109. ∠AOB = ∠A1OB;

∠AOB + ∠A1OB = 180°;

∠AOB = 90°.

Вправи 100 49

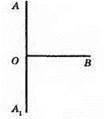
110. a)

Вправи 100 49

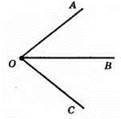
Ці кути мають спільну вершину;

Б) не обов’язково.

111. Обидва суміжні кути можуть бути тільки прямими.

112.

Вправи 100 49

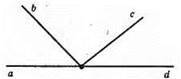
Суміжні

кути: ∠(ab) і ∠(bd); ∠(ac) i ∠(cd).

113.

Вправи 100 49

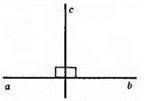
∠(ac) = ∠(bc) = 90°.

114. 150°, 120°, 90°, 45°.

115.

Вправи 100 49

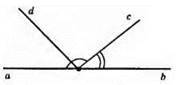
A) ∠(ac) і ∠(bc);

Б) ∠(ac) + (bc) = 180°;

В) ∠(ad) і ∠(db), ∠(ac) і ∠(bc).

116.

Вправи 100 49

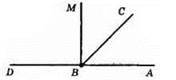
1) ∠ABC = 45°; б) ∠DBA = 180°.

117.

Вправи 100 49

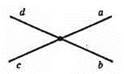
∠(ad) і ∠(ab); ∠(ab) і ∠(bc); ∠(bc) і ∠(cd); ∠(cd) i ∠(ad).

118.

Вправи 100 49

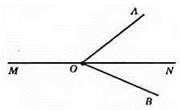
∠AON і ∠MOA; ∠NOB і ∠BOM – суміжні кути.

119.

Вправи 100 49

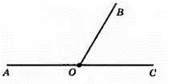
А) ∠BOC : ∠AOB = 5 : 31; x – спільна міра кутів, тоді ∠BOC = 5х, ∠AOB = 31x. ∠AOB + ∠BOC = 180°; 5x + 31x = 36°; 36x = 180°; x = 180° : 36; x = 5°; ∠AOB = 155°; ∠BOC = 25°.

Відповідь: 25°, 155°.

Б) ∠BOC < ∠AOB на 70°; ∠BOC = x, ∠AOB = x + 70°. x + x + 70° = 180°; 2x = 180° – 70°; 2x = 110°; x = 55°; ∠BOC = 55°, ∠AOB = 55° + 70° = 125°.

120.

Вправи 100 49

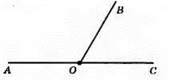
А) Нехай ∠BOC = x, тоді ∠AOB = 3x; ∠BOC + ∠AOB = 180°; x + 3x = 180°; 4x = 180°; x = 180° : 4; x = 45°; ∠BOC = 45°, ∠AOB = 3 x 45° = 135°.

Б) ∠BOC = x, ∠AOB = x + 20°; x + x + 20° = 180°; 2x = 160°; x = 160° : 2; x = 80; ∠BOC = 80°, ∠AOB = 80° + 20° = 100°.

121.

Вправи 100 49

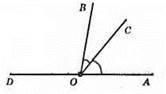
∠BOC = ∠COA = 50°, ∠AOB = 100°. ∠BOD – суміжний ∠AOB; ∠BOD + ∠AOB = 180°; ∠AOB = 180° – 100°; ∠AOB = 80°.

122. ∠1 > ∠3; ∠2 < ∠4.

Вправи 100 49

123.

Вправи 100 49

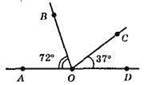
∠AOB = 72°, ∠COD = 37°, ∠BOC = 180° – 72° – 37° = 71°.

124.

Вправи 100 49

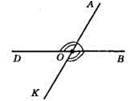
∠AOB – даний кут, ∠AOD і ∠BOK – суміжні з ним, ∠AOD = ∠BOK = 240° : 2 = 120°, ∠AOB = 180° – 120° = 60°.

Відповідь: 60°.

125.

Вправи 100 49

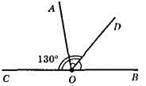
∠AOB – даний кут. OD – бісектриса ∠AOB. OB і ОС – доповняльні промені, ∠DOC = 130°. ∠DOB = 180° – 130° = 50°, ∠DOB = ∠DOA = 50°, ∠AOB = 2∠DOB = 50° х 2 = 100°.

Відповідь: 100°.

126.

Вправи 100 49

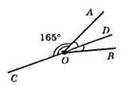
∠AOB – даний кут, OD – бісектриса даного кута, ОС і OD – доповняльні промені, ∠AOC = 165°. ∠AOD і ∠AOC – суміжні кути, ∠AOD = 180° – 165° = 15°, ∠AOD = ∠DOB = 15°, ∠AOB = ∠AOD +∠DOB = 15° + 15° = 30°.

Відповідь: 30°.

127.

Вправи 100 49

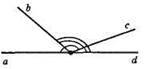
∠(ac) = 160°, ∠(bd) = 140°, ∠(cd) = 180° – 160° = 20°, ∠(ab) = 180° – 140° = 40°.

∠(bc) = 180° – (∠(ab) + ∠(cd)) = 180° – (40° + 20°) = 180° – 60° = 120°.

Відповідь: ∠(bc) = 120°.

128.

Вправи 100 49

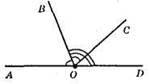
∠BOD = 112°, ∠AOC = 138°.

1) ∠AOB = 180° – ∠BOD = 180° – 112° = 68°;

2) ∠COD = 180° – ∠AOC = 180° – 138° = 42°;

3) ∠BOC = 180° – ∠AOB – ∠COD = 180° – 68° – 42° = 70°.

Відповідь: 70°.

129.

Вправи 100 49

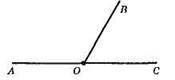
X – спільна міра кутів. ∠AOB – ∠BOC = 5x; ∠BOC = 2x; ∠AOB = 7x.

∠BOC + ∠AOB = 180°, 2x + 7x = 180°; 9x = 180°; x = 180° : 9; x = 20°; ∠BOC = 2 x 20° = 40°; ∠AOB = 7 x 20° = 140°.

Відповідь: 40° і 140°.

130.

Вправи 100 49

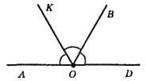
∠AOB – даний кут OK – бісектриса кута. ∠BOD і ∠AOB – суміжні, ∠KOB = ∠BOD, ∠KOB = ∠AOK, OK – бісектриса, отже, ∠AOK = ∠KOB = ∠BOD = 180° : 3 = 60°; ∠AOB = 120°.

Відповідь: 120°.

131.

Вправи 100 49

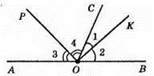
∠AOC і ∠COB – суміжні кути, OK – бісектриса ∠COB, ∠1 = ∠2, OP – бісектриса ∠AOC, ∠3 = ∠4.

(∠1 + ∠4) + (∠2 + ∠3) = 180°; ∠1 + ∠4 = ∠2 + ∠3; ∠1 + ∠4 = 90°; ∠POK = 90°.

Відповідь: 90°.

132.

Вправи 100 49

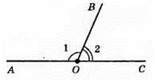
∠1 + ∠2 = 180°. OB – спільна сторона. ∠AOB і ∠COB – суміжні кут.

133.

Вправи 100 49

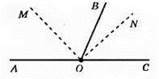
∠MON – 90°, ОМ і ON – бісектриси кутів ∠AOB і ∠BOC.

Ці кути суміжні, OB – спільна сторона, а ОС і ОА – доповняльні промені; точки А, О, С лежать на одній прямій.

134.

Вправи 100 49

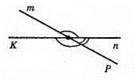
M i p, k i n – доповняльні промені.

135.

Вправи 100 49

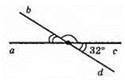
∠(cd) = 32°, ∠(ad) = 180° – 32° = 148°, ∠(ab)= 180° – 148° = 32°.

Відповідь: ∠(ab) = 32°, ∠(ad) = 148°.

136.

Вправи 100 49

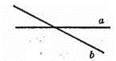
1) Дві прямі при перетині не можуть утворити три гострі кути.

2) Не можуть утворити тільки один тупий кут.

Вправи 100 49

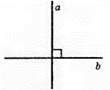
3) Можуть при перетині утворити чотири прямі кути.

137.

Вправи 100 49

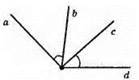
Два рівні кути зі спільною вершиною не завжди вертикальні.

138.

Вправи 100 49

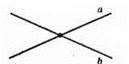
А) Вертикальні кути; б) суміжні кути; в) вертикальні кути.

139. Якщо прямі перпендикулярні.

140. Гострий кут.

141. Ці прямі – перпендикулярні.

142.

Вправи 100 49

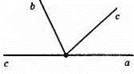
С може бути перпендикулярною до якої-небудь із прямих а і b.

143.

Вправи 100 49

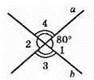
A) ∠1 = 80°, ∠2 = 80°, ∠3 = ∠4 = 100°;

Б)

Вправи 100 49

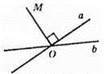
M ⊥ а, m не є перпендикулярною до прямої b.

144. c ⊥ a, b || c.

Вправи 100 49

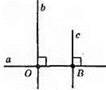
145.

Вправи 100 49

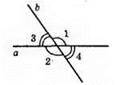
∠1 = 125°, ∠2 = ∠1 = 125°, ∠3 = ∠4 = 180° – 125° = 55°. Кут між цими прямими 55°.

146.

Вправи 100 49

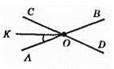
А) ОК – бісектриси ∠COA, ∠AOK = 23°, ∠COA = ∠DOB = 46°, ∠BOC = ∠AOD = 180° – 46° = 134°.

Відповідь: 46°. 46°, 134°, 134°.

Б) ∠BOC в 3 рази > ∠BOD; ∠BOD = х, ∠COB = 3х; х + 3х = 180° (суміжні кути); 4х – 180°; х = 180° : 4; х = 45°; ∠AOC = ∠BOD = 45°, ∠COB = ∠AOD = 135°.

147.

Вправи 100 49

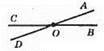
A) ∠AOC + ∠BOD = 320°, ∠AOC = ∠BOD (вертикальні кути). ∠AOC = ∠BOD = 320° : 2 = 160°; ∠AOВ і ∠AOC – суміжні кути; ∠AOВ = 180° – ∠AOC = 180° – 160° = 20°; ∠COD = ∠AOB = 20°.

Б)

Вправи 100 49

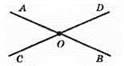
∠AOD більше ∠DOB на 50°; ∠DOB = x, ∠AOD = x + 50°. ∠AOD і ∠DOB – суміжні кути; x + x + 50° = 180°; 2x = 180° – 50°; 2x = 130°; x = 130° : 2; x = 65°; ∠AOC = ∠DOB = 65°; ∠AOD = ∠COB = 65° + 50° = 115°.

Відповідь: 65°, 65°, 115°, 115°.

148. AB ⊥ CD

Вправи 100 49

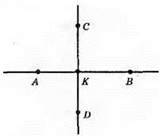
A) AK ⊥ CD, BK ⊥ CD, AB ⊥ CD;

6) KD ⊥ AK, KC ⊥ AK, CD ⊥ AK, DC ⊥ AK.

149.

Вправи 100 49

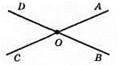
AC перетинається з прямою BD. ∠AOD – тупий, ∠COB = ∠AOD – вертикальні кути, ∠COB – тупий, ∠AOB – суміжний тупому куту, ∠AOB – гострий, ∠COD = ∠AOB, ∠COD – гострий кут.


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Вправи 150-175 150. ∠1 = 90°, ∠2 = ∠1 = 90° – вертикальні кути; ∠3 – суміжний куту ∠1. ∠3 = 180° – 90° = 90°, ∠3 = ∠4 = 90° (вертикальні кути). 151. ∠(ac) = 70°; ∠(ab) = 90°; ∠(bc) = 90° – ∠(ac) = 90° – 70° = 20°. 152. а ⊥ с; ∠(ab) = […]...

  2. Вправи 375-424 375. ВС – бісектриса ∠ABD; ∠ABD = 80° + 80° = 160°; ∠BAC + ∠ABD = 20° + 160° = 180°; ∠BAC і ∠ABD – внутрішні односторонні кути при прямих АС і BD та січній АВ. Отже, BD || АС. 376. ∠A = 70°, ∠B = 40°, BE – бісектриса ∠ABD; ∠DBE = ∠ABE = […]...

  3. Вправи для повторення до розділу 2 Розділ 2. Взаємне розміщення прямих па площині Вправи для повторення до розділу 2 До § 5. 226. На рис. 184 суміжні кути ∠2 і ∠3. на рис. 185 суміжні кути ∠1 і ∠4 та ∠2 i ∠3. На рис. 186 суміжні кути ∠1 і ∠2 та ∠3 i ∠4. 227. 1) Так, можна. Треба побудувати […]...

  4. Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих Розділ 2. Взаємне розміщення прямих па площині § 9. Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих 170. Рис. 119: ∠1 і ∠2 – внутрішні різносторонні кути. Рис. 120: ∠1 і ∠2 – відповідні кути. Рис,121: ∠1 i ∠2 – внутрішні різносторонні кути. 171. Внутрішні односторонні кути: ∠ANM і ∠NMB, ∠CNM і ∠NMD. […]...

  5. Вправи 325-374 325. ?ABC; AB = AC; ?A1B1C1; A1B1 = A1C1; ∠B = ∠B1; BK = B1K1. ∠AKB = ∠CKB = ∠A1K1B1 = ∠C1K1B1 = 90°. ?АВK = ?A1B1K1. 1) BK = В1K1; 2) ∠1 = ∠2; 3) ∠3 = ∠4, отже, AB =A1B1. ?АВС = ?А1В1С1. AB = A1B1; BC = В1С1; ∠B = ∠B1. 326. […]...

  6. Суміжні та вертикальні кути § 1. Найпростіші геометричні фігури та їхні властивості § 4. Суміжні та вертикальні кути Практичні завдання 86. ∠BAC – гострий, ∠OAB – суміжний до кута ВАС. ∠АОВ – прямий, ∠COA – суміжний до кута АОВ. ∠BOC – тупий, ∠AOB – суміжний до кута ВОС. 87. ∠AOC і ∠COB – суміжні. 88. а) ∠ABD i ∠CBD; […]...

  7. Вправи 275-324 275. Кут В. а) ВА = ВС, ?АВС – рівнобедрений, у нього дві сторони рівні; Б) ∠A = ∠C. 276. ∠A = 60°; AD – бісектриса кута А. BC ⊥ AD; AB = AC; ∠B = ∠C. 277. AB = ВС; АС – основа. Нехай АВ = ВС = х м, тоді АС = (х […]...

  8. Вправи 225-273 225. L ⊥ AB; X – точка прямої l; О – середина AB. ?АОХ = ?BOX (за першою ознакою рівності трикутників). 1) АО = OB; 2) ∠3 = ∠4 = 90°; 3) ОХ – спільна сторона. З цього випливає АХ = ВХ, отже, точка X рівновіддалена від кінців відрізка А і В. 226. Три прямі […]...

  9. Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною Розділ 2. Взаємне розміщення прямих па площині § 10. Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною 199. 1) ∠1 = ∠8, ∠6 = ∠3 (як відповідні кути при паралельних прямих а і b і січній с). 2) ∠2 = ∠4 (як внутрішні різносторонні кути при паралельних прямих а і b і […]...

  10. Вправи 176-224 176. Якщо три точки лежать на прямій, вони не можуть бути вершинами трикутника. 177. А) Кути прилеглі до сторони МР: ∠KMP і ∠KPM; Б) ∠KMP – протилежний стороні KP; В) сторона протилежна куту K – МР; В) сторони прилеглі до кута Р – KP і РМ. 178. Якщо два трикутники рівні, то їх периметри рівні. […]...

  11. Вправи 425-474 425. АС – основа; AB = CB; ∠ADC = 150°. ∠CAD = ∠BAD = x; ∠ACD = 2x; x + 2x + 150° = 180°; 3x = 180° – 150°; 3x = 30°; x = 10°; ∠C = ∠A = 20°; ∠B = 180° – (20° + 20°) = 140°. Відповідь: 20°, 20°, 140°. 426. […]...

  12. Вправи 475-524 475. ?ABC – прямокутний; ∠A = 30°; АС = 18 см; ВК – бісектриса, проведена до катета АС; ∠CBK = ∠ABK = ∠CBA : 2 = 60° : 2 = 30°; ∠CBA = 90° – ∠CAB = 90° – 30° = 60°; СК = х, тоді AK = 18 – х. ?АВК – прямокутний; ∠A […]...

  13. Вправи 525-574 525. АВ = CD; AO : OB = CO : OD; ?СОВ = ?AOD (за двома сторонами і кутом МІНІ ними). З рівності трикутників маємо: BC = AD. ?ВСА = ?DAC. 1) АС – спільна сторона; 2) AB = CD; 3) BC = DA; ∠MCA = ∠MAC; отже, ∠A = ∠C; ?CMА – рівнобедрений; МС […]...

  14. Суміжні й вертикальні кути Геометрія Основні властивості найпростіших геометричних фігур Суміжні й вертикальні кути Два кути називаються Суміжними, якщо в них одна сторона спільна, а інші сторони є доповняльними півпрямими. На рисунку і – суміжні. Властивості суміжних кутів Теорема 1. Сума суміжних кутів дорівнює . (Зверніть увагу: кути, сума яких дорівнює , не обов’язково суміжні.) Теорема 2. Коли два […]...

  15. Вертикальні кути Розділ 1. Найпростіші геометричні фігури та їх властивості § 5. Вертикальні кути 152. 1) ∠AYX і ∠BYZ – вертикальні; 2) ∠OLK і ∠MLN – не вертикальні. 153. 1) ∠AOD – вертикальний з кутом 1; 2) ∠АОС і ∠DOB – суміжні з кутом 1. 154. ∠BOA і ∠COD – суміжні. ∠BOA = ∠COD = 60°. 155. […]...

  16. Вертикальні кути. Кут між двома прямими, що перетинаються Розділ 2. Взаємне розміщення прямих па площині § 6. Вертикальні кути. Кут між двома прямими, що перетинаються 107. 1) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 15°, дорівнює 15°. 2) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 129°, дорівнює 129°. Відповідь: 1) 15°; […]...

  17. Зовнішній кут трикутника та його властивості Розділ 3. Трикутники. Ознаки рівності трикутників § 18. Зовнішній кут трикутника та його властивості 438. ∠BAK – зовнішній кут при вершині А. 439. ∠LDP – зовнішній кут при вершині D. 441. ∠A + ∠B = 70° – за властивістю зовнішнього кута трикутника. 442. Зовнішній кут трикутника при вершині С дорівнює 74° згідно з властивістю зовнішнього […]...

  18. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої Розділ 2. Взаємне розміщення прямих па площині § 7. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої 128. m ⊥ n, MN ⊥ АВ. 129. KA ⊥ c, ВМ ⊥ с. 130. ВL ⊥ a. MВ ⊥ a. 131. 1) Відрізки AB і MN перпендикулярні, оскільки вони лежать на перпендикулярних прямих a і b. 2) […]...

  19. Кути – ПЛАНІМЕТРІЯ Формули й таблиці МАТЕМАТИКА ПЛАНІМЕТРІЯ Паралельні прямі перетинають сторони кута. Кути Кут – плоска фігура, що складається із двох променів зі цільним початком й обмеженої ними частини площини. Промені називаються сторонами, їхня спільна точка – вершиною, обмежена ними частина площини – внутрішньою областю. α + α’ = 180° α і α’ – суміжні кути β […]...

  20. Перша та друга ознаки рівності трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 13. Перша та друга ознаки рівності трикутників 301. На рис. 227 трикутники рівні за першою ознакою (за двома сторонами і кутом між ними). На рис. 228 трикутники рівні за другою ознакою (за стороною і прилеглими двома кутами). 302. У? ABC і? CDA спільний елемент – сторона AВ. У? […]...

  21. Вправи 625-682 625. Геометричним місцем центрів кіл радіуса R, що проходить через дану точку А, є коло із центром в точці А і радіусом R. 626. Геометричним місцем центрів кіл, що дотикаються до сторін даного нерозгорнутого кута, є бісектриса даного кута без його вершини О. ОК – бісектриса. 627. Геометричним місцем точок С, які є вершинами трикутників […]...

  22. Коло і його елементи Розділ 4. Коло і круг. Геометричні побудови § 21. Коло і його елементи 578. PL – хорда, що проходить через центр кола, називається діаметром. 579. 1) 5 х 2 = 10(см); 2) 4,7 х 2 = 9,4 (дм). 580. 1) 8 мм х 2 = 16 мм; 2) 4,8 см х 2 = 7,6 см. […]...

  23. Вправи для повторення розділу 4 Розділ 4. Коло і круг. Геометричні побудови Вправи для повторення розділу 4 До § 21. 756. AB – діаметр, ОС – радіус. AD – хорда. 757. 1) Коло з променем ОК має одну спільну точку. 2) Коло з прямою ОК має дві спільні точки. 758. ?АОВ = ?ВОС за двома сторонами і кутом між ними […]...

  24. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника Розділ 3. Трикутники. Ознаки рівності трикутників § 15. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника 351. 1) AT – висота трикутника ABC. 2) AN – медіана трикутника ABC. 3) АР – бісектриса трикутника? AВС. 352. Оскільки AK – висота, то ∠BKA = ∠CKA = 90°. 353. Оскільки АК – бісектриса, то ∠BAK = […]...

  25. Пряма й обернена теореми Геометрія Основні властивості найпростіших геометричних фігур Пряма й обернена теореми Формулювання теореми складається з двох частин. В одній говориться про те, що дано. Ця частина називається Умовою. У другій частині говориться про те, що треба довести. Ця частина називається Висновком. Приклади 1) Якщо кути суміжні, то їх сума дорівнює 180°. Умова Висновок 2) У прямокутному […]...

  26. Вправи 1-49 1. А є ВС; В є АС. 2. А є с; В ∉ с. AB і с перетинаються в точці А. 3. Ці прямі мають тільки одну спільну точку А. 4. Точки В і С лежать по один бік від точки А. 5. а) Точка М лежить між L i N; Б) L і М […]...

  27. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 19. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників 466. 1) PF – гіпотенуза, PL і LF – катети. 2) PF довша за PL, PF довша за LF, оскільки PF – гіпотенуза. 467. На рис. 321 трикутники рівні за двома катетами. Оскільки АС = ML, СВ = LP, […]...

  28. Запитання і вправи для повторення § 7 Відповідь: (3; 3), (-1; -2), (1; 0,5). 1012. а) х – 2y = 4; X 0 4 Y -2 0 Б) 4х + у = -4; X 0 -1 Y -4 0 В) 3х – 2y = 6. X 0 2 У -3 0 Відповідь: пара чисел (-2; 3) не являється розв’язком системи рівнянь Х […]...

  29. Ознаки паралельності двох прямих § 3. Паралельні прямі. Сума кутів трикутника 13. Ознаки паралельності двох прямих Практичні завдання 300. 1) Кути АОМ і CEO – відповідні; 2) кути АОЕ і СЕК – відповідні; 3) кути АОE і OED – різносторонні; 4) кути АОЕ і CEO – односторонні. 1) відповідні; 2) односторонні; 3) різносторонні. 301. 1) ∠1 i ∠5; ∠2 […]...

  30. Вправи 575-624 575. АВ і АС дотикаються до кола з центром О у точках В і С. ∠CBO = 40°. ?АBО – прямокутний, OB ⊥ AB (OB – радіус, проведений в точку дотику). ?АСО – прямокутний (ОС – радіус, проведений в точку дотику). ∠ABO = 90°; ∠ACO = 90°; ?ВОС – рівнобедрений, OB = ОС; ∠OBC = […]...

  31. Властивості перетворення подібності Геометрія Подібність фігур Властивості перетворення подібності Теорема 1. Перетворення подібності переводить прямі у прямі, півпрямі – у півпрямі, відрізки – у відрізки. Теорема 2. Перетворення подібності зберігає кути між півпрямими. Із цього випливає, що перетворення подіб­ності переводить паралельні прямі в паралельні прямі. Дві фігури називаються Подібними, якщо вони переводяться одна в одну перетворенням подібності. Позначення: […]...

  32. Вправи для повторення розділу 1 До § 1. 617. Цілі раціональні вирази: Дробові раціональні вирази: А + с 618. 50а кг завезли цукру. Якщо а = 12, то 50а = 50 • 12 = 600 (кг). До § 2. 624. n, n + 1, n + 2 – три послідовні цілі числа; N + (n + 1) + (n + […]...

  33. Суміжні кути Урок № 10 Тема. Суміжні кути Мета: домогтися розуміння учнями змісту наслідків з теореми про суму суміжних кутів та змісту понять “наслідок”, “посилання”; використовуючи знання теореми про суміжні кути та її наслідки, виробити вміння розв’язувати задачі на обчислення та доведення, в яких йдеться про суміжні кути. Тип уроку: застосування знань, умінь та навичок. Наочність і […]...

  34. СУМІЖНІ І ВЕРТИКАЛЬНІ КУТИ Геометрія Евкліда є лише першим кроком до вивчення форм реального простору. О. Смогоржевський РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ У цьому розділі підручника ви розширите і поглибите свої знання про прямі і промені однієї площини, ознайомитеся з дуже важливими поняттями: суміжні кути, вертикальні кути, перпендикулярні прямі, паралельні прямі тощо, а також із важливими загальноматематичними […]...

  35. Властивості й ознака рівнобедреного трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 12. Властивості й ознака рівнобедреного трикутника 476. На мал. 72: ML і МК – бічні сторони, KL – основа, ∠K = ∠L. 477. KD = DF, КЕ = EF, ∠K = ∠F, ∠KDE = ∠FDE, ∠DEK = ∠DEF = 90°. 478. Щоб провести бісектрису, медіану і […]...

  36. Вертикальні кути. Кут між прямими Урок № 11 Тема. Вертикальні кути. Кут між прямими Мета: домогтися засвоєння учнями означення вертикальних кутів, формулювання і доведення теореми про властивість вертикальних кутів; означення кутів між прямими. Сформувати вміння: – будувати вертикальні кути; – знаходити вертикальні кути на рисунку; – розв’язувати задачі із застосуванням теореми про рівність вертикальних кутів та суму суміжних кутів. Тип […]...

  37. Прямокутник Геометрія Чотирикутники Прямокутник Прямокутник – це паралелограм, у якого всі кути прямі. Властивості прямокутника Оскільки прямокутник є паралелограмом, він має всі властивості паралелограма і ще деякі інші. Теорема. Діагоналі прямокутника рівні. На рисунку . . ; – рівнобедрені. Ознаки прямокутника Теорема 1. Якщо в чотирикутнику всі кути рівні, то він є прямокутником. Теорема 2. Якщо […]...

  38. Вправи для повторення розділу 3 До § 22. 1116. 1) х + 3 = 2; -5 + 3 = 2; -2 ≠ 2; ні; 2) 2 – х = 7; 2 – (-5) = 7; 7 = 7; -5 є коренем рівняння; 3) х : 5 = 1; -5 : 5 = 1; -1 ≠ 1; ні; 4) 4х = […]...

  39. Властивості кутів трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 10. Властивості кутів трикутника 344. ∠E = 60°, ∠F = 40°, ∠D = 80°. ∠E + ∠F + ∠D = 60° + 40° + 80° = 180°. 345. На мал. 208 неправильно сказано градусну міру кутів? АВС, оскільки? ABC – прямокутний, a ∠B + ∠C = […]...

  40. Кут. Вимірювання кутів. Бісектриса кута Розділ 1. Елементарні геометричні фігури та їхні властивості § 3. Кут. Вимірювання кутів. Бісектриса кута 33. 1) М – вершина кута, МА і МК – сторони кута АМК; 2) L – вершина кута, LP і LF – сторони кута PLF; 3) N – вершина кута, NB i NC – сторони кута BNC. 34. 1) O […]...

Ви зараз читаєте: Вправи 100-49
«
»