Вправи 575-624
575.
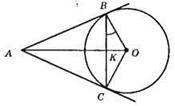
АВ і АС дотикаються до кола з центром О у точках В і С. ∠CBO = 40°.
?АBО – прямокутний, OB ⊥ AB (OB – радіус, проведений в точку дотику).
?АСО – прямокутний (ОС – радіус, проведений в точку дотику).
∠ABO = 90°; ∠ACO = 90°;
?ВОС – рівнобедрений, OB = ОС; ∠OBC = ∠OCB = 40°; ∠BOC =180°- (40° + 40°) = 100°. ?АВО = ?АСО – прямокутні (АО = CO; АО – спільна сторона).
∠AOB = ∠AOC = 100° : 2 = 50°;
?АВО; ∠BAO = 90° – 50° = 40°;
?АСО; ∠OAC = 90° – 50° = 40°;
∠BAC = ∠BAO + ∠CAO = 40° + 40° = 80°.
Відповідь:
576.
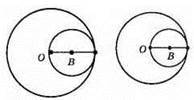
Радіус другого кола може бути: R = 10 – 8 = 2 (см); R = 10 + 8 = 18 (см).
577.
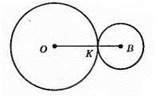
Два кола дотикаються зовнішньо. OB – відстань між центрами кіл.
OB = 8 см; OK = R1; KB = R2; d1 – діаметр одного кола, d2 – діаметр другого кола; d1 – d2 = 4 см; d1 + d2 = 2(R1 + R2) = 2 x 8 = 16 см.
Складемо систему рівнянь: 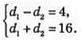
2d1 = 20; d1 = 20 : 2 = 10 см; d2 = 16 – 10 = 6 см.
Відповідь: 10 см і 6 см.
578.
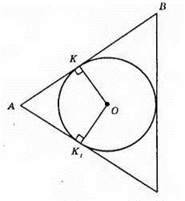
А) три дотичні до кола не можуть перетинатися в одній точці.
579.
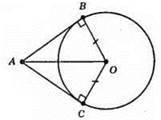
AB і АС дотикаються до кола із центром О в точках
?АСО – прямокутний ОС ⊥ АС (властивість дотичної).
?АВО = ?АСО (АО – спільна сторона; ВО = ОС – радіуси кола). З їхньої рівності маємо: ∠BOA = ∠COA = 120° : 2 = 60°.
?АВО; ∠BAO = 90° – 60° = 30°. ВО – катет, що лежить проти кута 30°,
ВО = 1/2АО = 1/2 • 30 = 15 (СМ).
Відповідь: 15 см.
580.
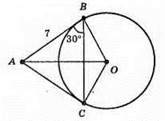
АВ і АС дотикаються до кола; AB = 7 см; ∠ABC = 30°; ?АВО = ?АСО – прямокутні (АО – спільна, OB = ОС). OB ⊥ AB, ОС ⊥ АС (властивість дотичних).
?ВОС – рівнобедрений OB = ОС; ∠CBO = ∠BCO = 90° – 30° = 60°; ∠BOC = (180° – 120°) : 2 = 30°.
?АВО; ∠BOA = 30°, АВ – катет, що лежить проти кута 30°, АВ = 1/2АО; АО = 14 см.
Відповідь: 14 см.
581. а) R1 = 5; R2 = 2 і d = 1. R1 – радіус першого кола; R2 – радіус другого кола; d – відстань між їх центрами; R3 – радіус третього кола. R3 = 1; R3 = 2; R3 = 3; R3 = 4;
Б) якщо R1 = 3; R2 = 4; d = 5, то R3 = 1; R3 = 2; R3 = 3; R3 = 6.
582. а)
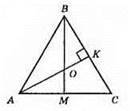
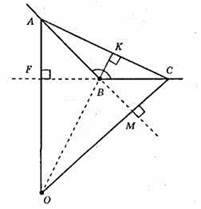
?АВС – рівносторонній. AB = ВС = АС; ∠A = ∠B = ∠C = 60°. ВМ i АК – медіани висоти і бісектриси; ?ВОК – прямокутний AK ⊥ ВС; ∠MBC = 30°; ВМ – бісектриса; ∠BOK = 90° – 30° = 60°; ∠BOK – кут між медіанами ВМ i АК;
Б) ВМ – відстань від вершини В до АС; АК – відстань від вершини А до сторони ВС. Відстані від вершин до прямих, що містять протилежні сторони рівностороннього трикутника, рівні, бо ці відстані – висоти рівностороннього трикутника, а у рівносторонньому трикутнику всі висоти рівні.
583. а)
Б)
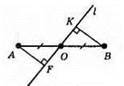
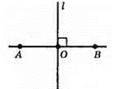
L перетинає відрізок AB у його середині.
А) якщо l ⊥ AB, то АО = OB. АО і OB – відстань від А і В до l. AF ⊥ l, ВК ⊥ l; АF i ВК – відстані від точок А і В до прямої l. ?AOF = ?ВОК – прямокутні; АО = OB; ∠AOF = ∠BOK (вертикальні кути). З рівності трикутників маємо: FР = ВК.
584. а) спочатку поділити відрізок на 2 частини, потім кожну частину ще поділити на 2 частини, відрізок буде поділено на 4 рівні відрізки;
Б) поділити кут на 2 частини, а потім кожний кут поділити ще на 2 рівні частини.
585. а) кут 90° поділити на 2 частини; б) кут 180° поділити на 4 рівні частини; 3/4 кута становить 135°.
587. а < b
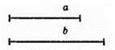
А) 3а, відкласти послідовно 3 рівних відрізки довжиною а;
Б) b – а; відкласти від початку відрізка b, відрізок а;
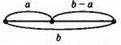
В) відрізок а, послідовно відкласти 2 відрізки довжиною b.
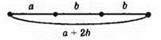
588.
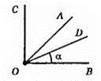
А) кут β поділити на 2 рівних кути;
Б) від заданого променя відкласти кут α; від сторони кута α відкласти кут β;
В) побудувати кут β = ∠AOB, від променя ОА відкласти ∠AOC = β. Від променя OB відкласти ∠BOD = α. ∠DOC = 2β – α.
589.
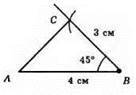
1) Побудувати AB = 4 см;
2) ABC = 45°; на промені ВС, відрізок ВС = 3 см.
590.
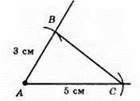
1) Побудувати ∠BAC = 60°. На сторонах кута відкласти відрізки АС = 5 см; AB = 3 см.
591.
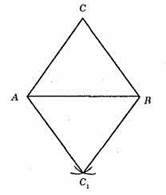
Із точки А як із центра побудувати частину кола радіуса АС, із точки В як із центра побудувати частину кола радіусом ВС. С1 – точка перетину дуг цих кіл, ?АВС = ?АВС1.
592. а)
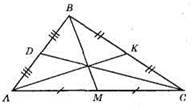
ВМ, АК, CD – медіани трикутника АВС, точки К, М, D – середини сторін трикутника;
Б)
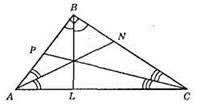
BL, BP, AN – бісектриси трикутника, ділять кути трикутника навпіл;
В)
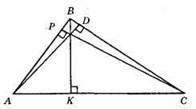
ВК ⊥ АС, CP ⊥ AB, AD ⊥ ВС; CP, AD, ВК – висоти? АВС;
Г) ?ABC – тупокутний; ВК ⊥ AC, CM ⊥ AB, AF ⊥ ВС; О – точка перетину висот AF, ВК, CM.
593. a)
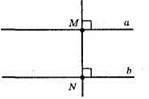
A || b, MN – відстань між двома паралельними прямими.
Б)
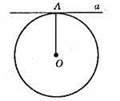
А – дотична, А – точка дотику; ОА – радіус, проведений в точку дотику; ОА ⊥ а.
594. Побудувати кут 120°, поділити променем на 2 частини за допомогою циркуля. 120° : 2 = 60°.
596.
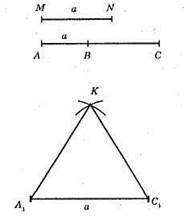
1) Побудували A1C1 = а;
2) На відрізку АС = Р (Р – периметр) побудували AB = а; ВС = 2А1К;
3) Поділили відрізок ВС навпіл;
4) Коло із центром в точці А1 і радіусом 1/2BC;
5) Коло із центром в точці С1 і радіусом 1/2B.
?А1КС1 – рівнобедрений з основою а і периметром Р.
597.
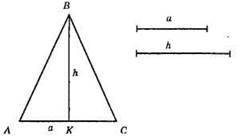
1) Побудували відрізок АС = а;
2) Поділили АС навпіл; АК = ВС;
3) Через точку К провели пряму перпендикулярно АС, від точки К відкладемо ВК = h.
?ABC рівнобедрений з основою а та висотою h.
598.
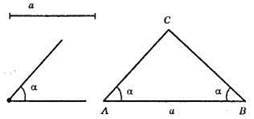
1) AB = а; 2) від т. А кут САВ = α; 3) від т. А кут СВА = α; 4) ?АВС – рівнобедрений з основою а та кутом при основі α.
599.
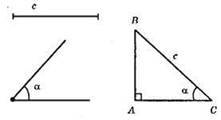
1) Побудували ∠BAC = α; 2) На сторони кута АВ = с; 3) Із точки В провели ВС перпендикулярно до другої сторони кута; 4) ?АВС – прямокутний із гіпотенузою С і гострим кутом α.
600.
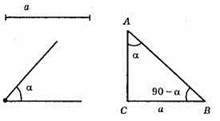
1) Побудуємо прямий кут MNP. Від сторони NP відкладемо ∠KNP = α; ∠MNK = 90° – α;
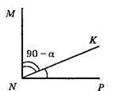
2) Побудуємо прямий ∠C;
3) На стороні кута відкладемо ∠CBA = 90° – α;
4) ?АВС – прямокутний з катетом ВС = а і гострим кутом α.
601.
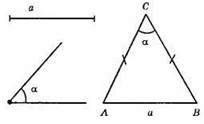
1) Побудуємо розгорнутий кут MNP;
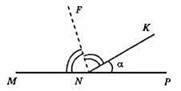
2) Від променя NP відкладемо кут ∠KNP = α;
3) Поділимо ∠MNK навпіл.
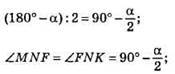
4) Побудуємо відрізок AB; AB = а; від променя AB відкладемо кут ∠CAB = ∠MNF, від променя ВА відкладемо ∠CBA = ∠MNF;
5) ?ABC – рівнобедрений з основою а та кутом а, протилежним основі.
602.
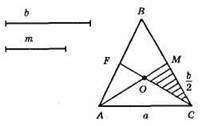
1) АВ = ВС = b; AM = FC = m; АО : ОМ = CO : OF = 2 : 1. За допомогою теореми Фалеса розділимо відрізок т на 3 рівні частини;
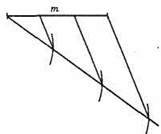
2) Побудуємо відрізок ВС = b (бічна сторона). Знайдемо середину М. Побудуємо? МОС за трьома сторонами.
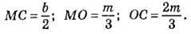
Побудуємо? FOA = ?МОС; з’єднаємо АС. Продовжимо AF і CM до перетину в точці В. ?ABC – шуканий трикутник.
603.
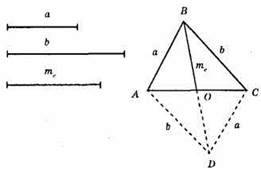
1) Відкладемо відрізок ВО = mс і подвоїмо його, BO = OD = 2mс;
2) Із кінців відрізка проведемо коло радіусом DC = a; DA радіусом b;
3) ?ABC – трикутник із сторонами а і b і медіаною mс.
604.
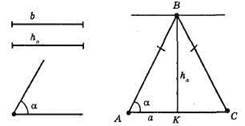
1) сторона АС = а;
2) проведемо на відстані ВК = ha пряму, паралельну даній стороні АС = а;
3) ∠BAC = α;
4) з’єднаємо В і С;
5) ?АВС зі стороною АС, прилеглим до неї кутом а і висотою, проведеною до цієї сторони.
605.
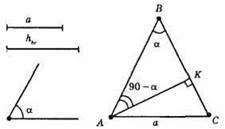
1) ВС – пряма; 2) АК ⊥ ВС; 3) AK = hHC;
4) AС = а;
5) від променя АК побудуємо ∠КАВ = 90° – α;
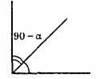
6) ?АВС, сторона АС = а; АК = hHC; ∠B = α.
606.
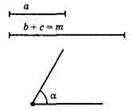
Розв’язок можливий, якщо а < m, бо а < b + с в будь-якому трикутнику.
Побудуємо? BCD, ВС = a; BD = m; ∠B = α. Проведемо серединний перпендикуляр від CD, він перетинає BD в точці A, AD = АС. Отримаємо? BCD, де ВС = a, ∠B = α, AB + АС = m, бо АС = AD.
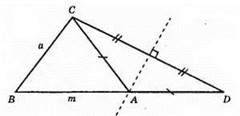
Доведемо, що серединний перпендикуляр перетинає BD. Припустимо, а перетинає сторону ВС в точці М, а пряму BD в точці К, якщо KB > BD, то ∠KCD < ∠BCD.
За властивістю серединного перпендикуляра? DKC – рівнобедрений, отже, ∠KCD = ∠D, але ∠D > ∠BCD, так як m > а, тоді ∠D < ∠C. Прийшли до суперечності, отже, D перетинає BD.
607.
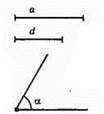
Задача має розв’язок, якщо d < а, |АС – АВ| = d.
1)
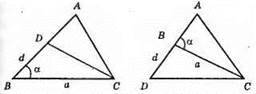
α – гострий кут. Якщо AB > АС, d = AC, відкладемо на стороні AB відрізок BD = d, тоді AD = AB – d = AC, тобто точка А лежить на серединному перпендикулярі до CD.
Якщо АС > AB, то відкладемо на продовженні сторони AB відрізок BD = d, d = АС – AB; AD = АВ + BD = AB + d, тобто AD = АС, тому точка буде належати серединному перпендикуляру до CD.
2) α – тупий кут. АС > AB, тоді на продовженні сторони AB відкладемо BD = d, тоді AD = АС і точка А лежить на серединному перпендикулярі до CD.
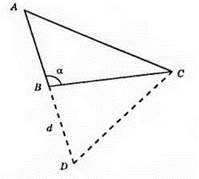
А) α – гострий кут, α = АС – AB. Побудуємо ∠B = α, відкладемо на одній стороні кута ВС = а, а на доповняльному промені до другої сторони BD = d.
Знайдемо точку А (проведемо серединний перпендикуляр до сторони CD, бо AB = AD – DB = АС – d, то d = АС – AB; ?ABC – шуканий.
Б) α – гострий кут; d = AB – АС. Побудуємо ∠B = d. Відкладемо на одній стороні кута ВС = а, а на другій BD = d.
Знайдемо точку А, провівши серединний перпендикуляр до відрізка CD, бо BA = d + АС, d = AB – АС, ?АВС – шуканий.
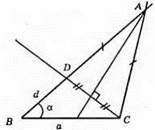
Якщо α – тупий кут, d = АС + АВ.
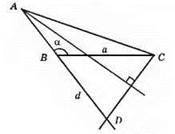
608.
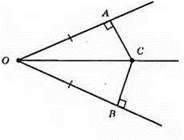
А) ∠AОВ; ОА = OB; АС ⊥ ОА; ВС ⊥ OB, Доведемо, що ОС – бісектриса цього кута.
?АОС = ВОС – прямокутні; ОС – спільна сторона, OB = ОА. З рівності трикутників маємо: ∠АОС = ∠ВОС, отже, ОС – бісектриса ∠AОВ.
609.
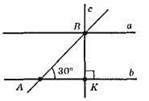
A || b, c – січна. AB = 22 CM, BK ⊥ a, ВК ⊥ b. ВК – відстань між паралельними прямими. ?АВК – прямокутний, ВК – катет, що лежить проти кута ∠BAK = 30°, ВК = 1/2АВ;
ВК = 1/2 • 22 = 11 см.
Відповідь: 11 см.
610. а) ні; б) ні; в) так.
611. а) ні; б) так.
612. в) ні.
613. а) так.
614.
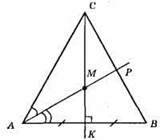
А) Геометричним місцем точок, рівно – віддалених від вершин А і В, є серединний перпендикуляр до сторони AB – СК ⊥ AB;
Б) геометричним місцем точок рівновіддалених від сторін АС і AB буде бісектриса кута САВ, АР – бісектриса;
В) М – точка перетину побудованих геометричних місць.
615. Дано колос центром О і хордою АВ. а) геометричним місцем точок, рівновіддалених від точок А і В, є пряма OK ⊥ AB, що проходить через середину AB, ця пряма проходить через точку О;
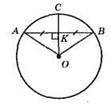
Б) геометричне місце точок кола, рівновіддалених від сторін кута ∠AOC, є бісектриса цього кута, на колі це точка С.
616.
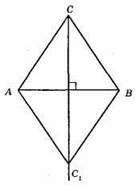
Геометричне місце точок, рівновіддалених від точок А і В, є серединний перпендикуляр до відрізка AB. AB = АС = ВС; AB = AC1 = BC1, ?АВС і? АВС1 – рівносторонні.
618.
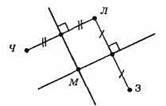
Точка, рівновіддалена від Чернігова, Луцька і Запоріжжя, – точка М перетину серединних перпендикулярів до відрізків, що з’єднують ці міста.
619. a)
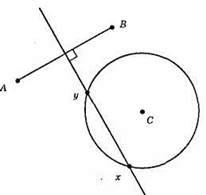
Б)
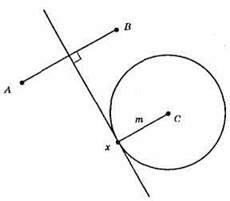
В)
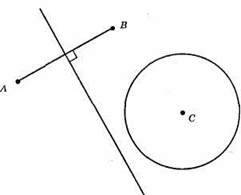
Дано: точки А, В, С. Побудувати точку, що рівновіддалена від точок А і В і лежить на заданій відстані від точки С. Точки, що рівновіддалені від точок А і В, належать серединному перпендикуляру до відрізка AB. Геометричним місцем точок, що лежать на заданій відстані т від точки С, є коло радіуса m. Таких точок, що рівновіддалені від точок А і В і лежать на заданій відстані від точки С, може бути: а) дві: х і у; б) одна: х; в) жодної.
620.
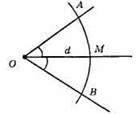
Геометричним місцем точок, рівновіддалених від сторін даного кута, є бісектриса цього кута. Геометричним місцем точок, які знаходяться на відстані d від вершини О, є коло із центром О і радіусом d. Точка перетину кола і бісектриси – точка М.
621.
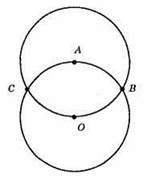
Точки B i С віддалені від точки А на відстань R. В і С – точки перетину кіл із центрами в точках А і О і радіусами R.
622.
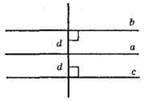
Геометричним місцем точок, рівновіддалених від даної прямої а на відстань d, є дві прямі, паралельні а й віддалені від неї на d. а || b; а || с.
623.
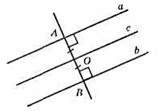
Геометричним місцем точок, рівновіддалених від двох паралельних прямих, є пряма, яка паралельна цим прямим (с || а; с || b) і проходить через середину спільного перпендикуляра. AB ⊥ а, AB⊥ b, АО = OB.
624.
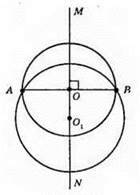
Геометричним місцем центрів кіл, що проходять через точки А і В. є серединний перпендикуляр до відрізка AB. MN ⊥ АВ.