Вправи для повторення розділу 4
Розділ 4. Коло і круг. Геометричні побудови
Вправи для повторення розділу 4
До § 21.
756.
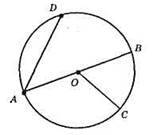
AB – діаметр, ОС – радіус. AD – хорда.
757.
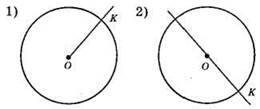
1) Коло з променем ОК має одну спільну точку.
2) Коло з прямою ОК має дві спільні точки.
758. ?АОВ = ?ВОС за двома сторонами і кутом між ними (ОА = OB, OB = ОС – як радіуси кола, ∠АОВ = ∠ВОС – за умовою).
Із рівності трикутників випливає, що AB = ВС.
759. ∠АОК – зовнішній кут до кута KOB. ∠АОК = 180° – 130° = 50°.
?АОК – рівнобедрений,
?KOB – рівнобедрений, оскільки ОК = OB – як радіуси, тоді ∠ОКВ = ∠ОВК = (180° – 130°) : 2 = 25°.
?АКВ – прямокутний, оскільки діаметр видно з будь-якої точки кола під кутом 90°. Отже, ∠АКВ = 90°. Отже, ∠А = 65°, ∠К = 90°, ∠B = 25°.
Відповідь: 25°, 65°, 90°.
760.
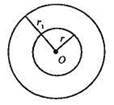
Кінці радіусів кола утворюють коло з тим самим центром і радіусом, вдвічі більшим від даного радіуса.
761.
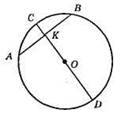
Нехай AB – дана хорда. За допомогою косинця проведемо діаметр CD ⊥ AB. Тоді за
762.
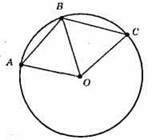
Нехай AB = ВС = ОС = ОА, тоді? АОВ і? ВОС – рівносторонні.
∠A = ∠AОВ = ∠АВО = 60°. ∠С = ∠ОВС = ∠ОСВ = 60°. ∠АВС = ∠АВО + ∠ОВС = 60° + 60° = 120°.
Відповідь: 120°.
763. AB – діаметр. ∠АКВ = 90°, оскільки діаметр кола видно з будь-якої точки кола під кутом 90°.
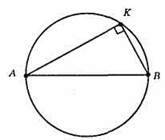
Нехай ∠КАВ = х°, тоді ∠КВА = 4х°. х + 4х = 90°; 5х = 90°; х = 18°. Отже, ∠А = 18°, ∠B = 18° х 4 = 72°.
Відповідь: 18°, 72°, 90°.
764.
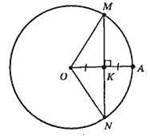
Нехай ОК = АК, MN ⊥ ОА.
З? ОМК: ∠ОРК = 30°, оскільки OK = 1/2ОМ. ?MON – рівнобедрений, оскільки ОМ = ON – як радіуси, тоді ∠ONM = ∠OMN = 30°, ∠MON = 180° – ∠ONM – ∠OMN = 180° – 30° – 30° = 120°. Отже, в? MON ∠MON = 120°, ∠OMN = 30°, ∠MNO = 30°.
Відповідь: 30°, 30°, 120°.
765.
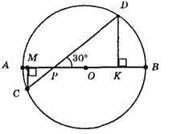
Нехай DK ⊥ АВ, CM ⊥ АВ, ∠DPB = ∠CPM = 30°, PD = 7 CM.
З прямокутного? DKP:
DK = 1/2РD = 1/2 • 7 = 3,5 CM.
З прямокутного? CMP:
MC = 1/2CP = 1/2 • 1 = 0,5 CM.
Відповідь: 0,5 см; 3,5 CM.
До § 22.
766.
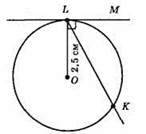
767.
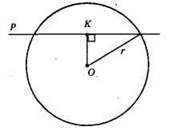
1) Пряма р перетинає коло, оскільки ОК < r, 12 см < 14 см.
2) Пряма р дотикається до кола, оскільки ОК = r, 7 см = 70 мм.
3) Пряма р не має спільних точок з колом, оскільки ОК > r, 2 дм > 18 см.
4) Пряма р перетинає коло, оскільки ОК < r, 0,3 дм < 32 мм.
768.
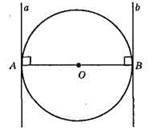
Нехай а і b – дотичні, тоді а ⊥ AB, b ⊥ AB, а || b. Отже, дотичні до кола, проведені через кінці діаметра, не перетинаються.
769.
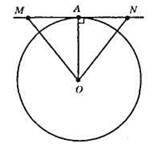
Нехай MN – дотична до кола, тоді ОА ⊥ MN (оскільки дотична до кола є перпендикулярною до радіуса, який проведений в точку дотику).
?АОМ = ?AON за двома катетами (ОА – спільний катет, AM = AN – за умовою). Із рівності трикутників випливає, що ОМ = ON.
770.
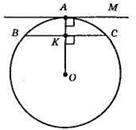
Оскільки ВК = КС, то ВС ⊥ ОА. Оскільки М – дотична, то AM ⊥ ОА.
Оскільки ВС ⊥ ОА і АМ ⊥ ОА, то ВС || AM. Отже, дотична, проведена через кінець радіуса, паралельна даній хорді.
До § 23.
771.
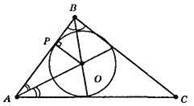
Оскільки центром кола, вписаного у трикутник, є точка перетину бісектрис цього трикутника, то за допомогою транспортира побудуємо бісектриси кутів А і В. Проведемо OP ⊥ AB – це і буде радіус вписаного кола. За допомогою циркуля вписуємо коло з центром у т. О радіусом ОР.
772.
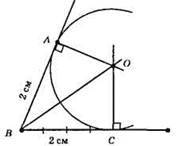
Будуємо бісектрису кута B. На сторонах кута відкладаємо відрізки ВС = ВА = 2 см. З точок С і А за допомогою косинця будуємо перпендикуляри до перетину у точці A. За допомогою циркуля вписуємо коло з центром у т. О радіусом, який дорівнює ОА.
773.
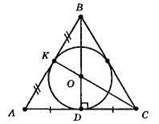
Нехай BD і СК – медіани, О – центр кола, вписаного в? ABC.
Оскільки О – точка перетину бісектрис, то BD і СК – бісектриси, медіани і висоти, а бісектриси, медіани і висоти співпадають тільки в рівносторонньому трикутнику. Отже, ?ABC – рівносторонній.
774.
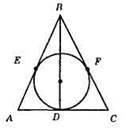
Нехай? ABC – рівнобедрений (AB = СВ), Е, F, D – точки дотику. За умовою ЕА : ЕВ = 2 : 3. Нехай ЕА = 2х, ЕВ = 3х. Враховуючи рівність відрізків дотичних, проведених з однієї точки до кола, маємо: P? ABC = AB + ВС + СА = (2х + 3х) + (3х + 2х) + (2х + 2х) = 14х. За умовою Р = 70 см, отже, 14х = 70 см, х = 5 см. Тоді AB = ВС = 2х + 3х = 5х = 5 х 5 = 25 (см), АС = 2х + 2х = 4х = 4 х 5 = 20 (см).
Відповідь: 25 см, 25 см, 20 см.
До § 24.
775.
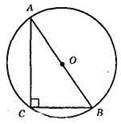
?ABC – прямокутний. О – центр кола – середина гіпотенузи.
776.
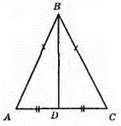
Центр описаного кола лежить на серединних перпендикулярах до сторін трикутника. Нехай? ABC – рівнобедрений (AB = ВС), BD ⊥ AC, тоді AD = DC, оскільки висота, проведена до основи є медіаною. Маємо BD ⊥ АС і AD = DC, отже, DB належить серединному перпендикуляру до основи АС.
777.
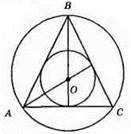
Нехай? ABC – рівносторонній. Точка О – центр вписаного кола в рівносторонній трикутник, отже, точка О – точка перетину бісектрис трикутника ABC. Оскільки в рівносторонньому трикутнику бісектриси є висотами і медіанами, то бісектриси лежать на серединних перпендикулярах до сторін трикутника, які перетинаються в т. О. Отже, центр кола, описаного навколо рівностороннього трикутника, збігається з центром кола, вписаного в цей трикутник.
До § 25.
778.
1)
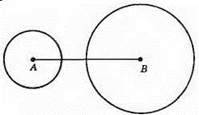
AB = 4 CM. Кола не перетинаються.
2)
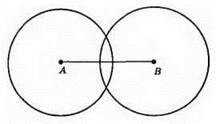
АВ = 4 см. Кола перетинаються.
779.
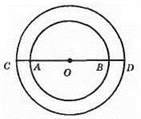
Нехай СА = 3 см, AB = 8 CM, BD = 3 см.
АО = АВ : 2 = 8 см : 2 = 4 см.
СО = СА + АО = 3 см + 4 см = 7 см.
Відповідь: 4 см, 7 см.
780. Нехай OB = 10x. ОА = 7x. AB = OB – ОА = 10x – 7х = 3x. За умовою 3x = 12 см, х = 4 см. Тоді OB = 10 х 4 = 40 (см), ОА = 7 x 4 = 28 (см).
Відповідь: 40 см, 28 см.
781.
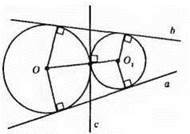
Три спільні дотичні можна провести до кіл, які мають зовнішній дотик.
782. І випадок. Кола мають зовнішній дотик.
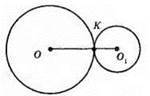
Нехай O1K = 5x, OK = 3x, тоді 5х + 3х = 16; 8x = 16; х = 2. Отже, O1K = 5 x 2 = 10 (см), ОК = 3 x 26 (см).
Відповідь: 10 см, 6 см.
II випадок. Кола мають внутрішній дотик.
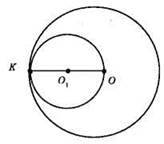
Нехай OK = 5х, О1К = 3х. Тоді O1O = OK – O1K = 5х – 3х = 2х; 2х = 16; х = 8. Отже, ОК = 5 х 8 = 40 (см), О1К = 3 х 8 = 24 (см).
Відповідь: 40 см, 24 см.
До § 26.
783.
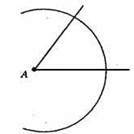
Коло перетне кожну зі сторін.
784.
АВ = ВС.
785.
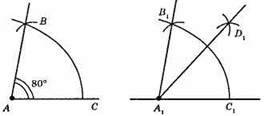
1) Проведемо промінь A1D.
2) Описуємо кола рівних радіусів із центрами А і A1. Одне коло перетинає сторони кута А в точках В і С, друге перетинає промінь AD в точці С1.
3) Описуємо коло із центром С1 і радіусом СВ. Точка В1 – точка перетину побудованих кіл.
4) Проводимо промінь A1B1.
5) Кут В1А1С1 – шуканий.
6) Радіусом з п. 2) точок С1 і В1 опишемо дуги у внутрішній області кута до їхнього перетину, отримаємо т. D1. Проведемо промінь А1D1 – бісектрису.
786.
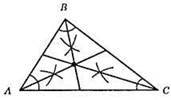
З кожної вершини кутів проведемо дугу кола довільного радіуса. З точок перетину дуг зі сторонами кутів проведемо дуги тим самим радіусом до їхнього перетину. Проведемо промені через вершини кутів і отримані точки перетину. Проведені промені – бісектриси кутів.
787.
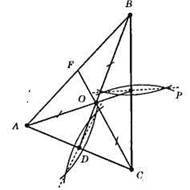
1) 3 точки А радіусом циркуля, більшим за половину сторони АС, опишемо дугу.
2) 3 точки С тим же радіусом циркуля опишемо дугу до перетину з першою дугою.
3) Через точки перетину дуг проведемо пряму, яка перетинає сторону АС в точці/).
4) Проведемо BD – медіану. Аналогічно робимо побудови для інших сторін трикутника. Отримані медіани BD, CF і АР – перетинаються в точці О.
788. 1) Поділимо ∠BAC навпіл, а потім ∠BAD навпіл. ∠BAF = 1/4∠BAC.
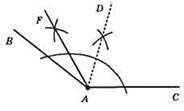
2)
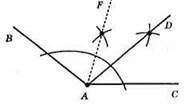
Поділимо ∠BAC навпіл, а потім ∠FAC навпіл. ∠BAD = 3/4∠BAC.
789.
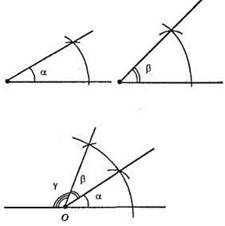
γ – третій кут трикутника.
1) Від довільного променя відкладемо кут α.
2) Від сторони кута а відкладемо кут β.
3) Кут, суміжний з кутом α + β, буде шуканим.
790.
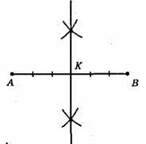
Нехай АВ – гіпотенуза.
1) Накреслимо коло радіуса АК = AB/2.
2) Проведемо діаметр АВ.
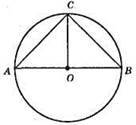
3) До AB в т. О будуємо перпендикуляр. Точка С його перетину з колом визначає шуканий? АВС (АС = ВС), ∠ACB = 90°.
791.
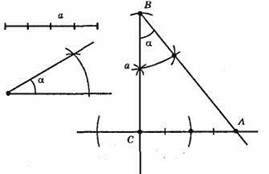
1) Будуємо прямий кут.
2) На одній стороні кута відкладемо відрізок, що дорівнює α.
3) Від променя ВС відкладемо кут, що дорівнює куту α.
4) ?АВС – шуканий.
792.
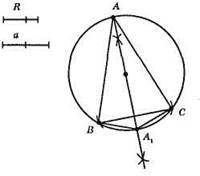
1) Будуємо коло з центром О і з радіусом R.
2) 3 довільної точки В будуємо коло з радіусом а, яке перетне побудоване коло в точці С.
3) Будуємо серединний перпендикуляр до ВС, який перетне коло у точках А і А1.
793. 1) Побудуємо відрізок АС = b.
2) Від променя АС відкладемо кут α.
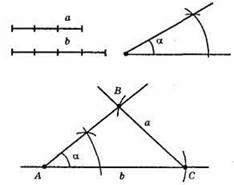
3) Точка В – точка перетину кола з центром у т. С і радіуса а і променя АВ.
4) ?ABC – шуканий.
794.
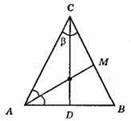
1) Слід побудувати кути 180° – β,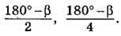 
2) Побудувати? АМС за стороною AM = l та кутами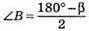 
і 
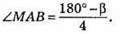
3) Провести промінь ВМ та серединний перпендикуляр CD до сторони AB, які перетнуться в точці С.
4) ?ABC – шуканий.
795.
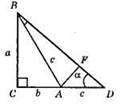
1) Будуємо прямокутний трикутник BCD за катетами ВС = a, CD = b + с.
2) Проводимо серединний перпендикуляр до сторони BD, який перетне сторону CD в точці А.
3) ?ABC – шуканий.
Дійсно, оскільки точка А належить серединному перпендикуляру, то AD = AB = с, тоді АС = b, ВС = а.
До § 27.
796.
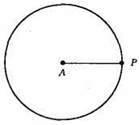
Геометричне місце точок, рівновіддалених від даної точки О на задану відстань ОР – коло з центром у точці О і радіусом ОР.
797.
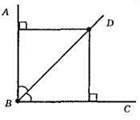
Геометричним місцем точок, рівновіддалених від сторін прямого кута ABC, є бісектриса BD.
798.
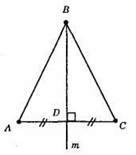
Пряма m, що містить висоту BD рівнобедреного трикутника ABC (AB = ВС), яка проведена до основи, є серединним перпендикуляром до відрізка АС (оскільки висота рівнобедреного трикутника, проведена до основи, є медіаною). Отже, пряма m є геометричним місцем точок, рівновіддалених від кінців основи.
799.
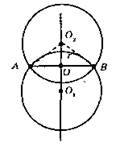
Центри побудованих кіл лежать на серединному перпендикулярі, проведеному до відрізка, що з’єднує дві дані точки A i В.
Якщо радіус кола менший від AB/2, то задача розв’язків не має.
Якщо r = AB/2, то задача має один розв’язок.
Якщо r > AB/2, то задача має два розв’язки.
800.
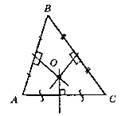
Геометричним місцем точок, рівновіддалених від усіх вершин трикутника ABC, є точка О – центр кола, описаного навколо? ABC.
801.
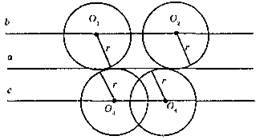
Геометричним місцем центрів кіл радіуса r, що дотикаються до прямої а, є дві прямі (які лежать по різні боки від прямої а), які паралельні прямій а і віддалені від прямої а на r.
802.
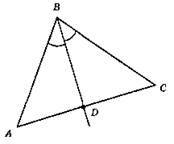
Оскільки точки, рівновіддалені від сторін кута, лежать на бісектрисі кута, то шукана точка D – точка перетину бісектриси кута, утвореного сторонами трикутника, і третьої сторони.
803.
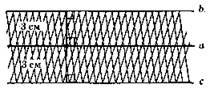
Геометричним місце точок, що знаходяться на відстані, яка не перевищує 3 см від заданої прямої а, є смуга, утворена паралельними прямими b і с, які паралельні прямій а і знаходяться від неї на відстані 3 см.
804.
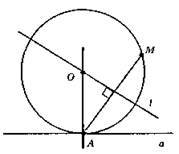
Центр кола знаходиться в точці перетину серединного перпендикуляра l до відрізка AM і прямої ОА, яка перпендикулярна до прямої а.
805.
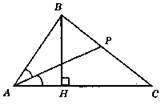
1) Будуємо прямокутний трикутник АВН, у якого катет ВН дорівнює висоті шуканого трикутника, а кут А дорівнює даному куту.
2) Проводимо бісектрису кута ВАН.
3) Точка Р – точка перетину прямої ВР і променя АР.
4) ?АВС – шуканий.
806.
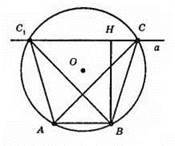
Будуємо коло за заданим радіусом.
2) Від довільної точки А відкладемо відрізок AB, який дорівнює стороні.
3) Проводимо пряму а, яка паралельна стороні AB і знаходиться на відстані, що дорівнює висоті шуканого трикутника.
4) Точки С і C1 – точки перетину прямої а і кола.
5) ?ABC і? ABC1 – шукані трикутники.
Завдання для перевірки знань за курс геометрії 7 класу
1.
A є m, B ∉ m.
2.
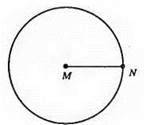
3.
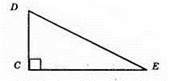
DE – гіпотенуза, CD і СЕ – катети.
4.
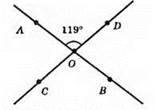
∠COB = ∠AOD = 119° – як вертикальні кути.
∠АОС = ∠DOB = 180° – 119° = 61° (за теоремою про суміжні кути).
Кут між прямими AB і CD дорівнює 61 °.
61°, 61°, 119°, 119°.
5.
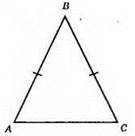
Нехай? ABC – рівнобедрений, AB = ВС = 9 см, Р? ABC = 24 см, тоді АС = Р? ABC – (AB + BC)= 24 – (9 + 9) = 24 – 18 = 6 (см).
Відповідь: 6 см.
6. ?CDN = ?MND за першою ознакою рівності трикутників, оскільки DC = MN – за умовою, ∠CDN = ∠DNM – за умовою, DN – спільна сторона.
7.
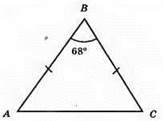
Нехай? ABC – даний трикутник, ∠B = 68°.
Нехай ∠A = х°, тоді ∠C = х° + 14°. ∠A + ∠B + ∠C = 180°, x + 68° + x 14° = 180°; 2х = 98; х = 49. Отже, ∠A = 49°, ∠C = 49° + 14° = 63°.
Відповідь: 49°, 63°.
8. Відкладемо відрізок AB = 6 см. Від т. А і В відкладемо кут ∠A = 50° і ∠B = 60°. ?ABC – шуканий.
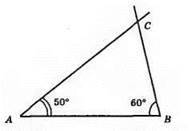
9. Нехай у прямокутному трикутнику ABC (∠C = 90°) ∠A = x°, тоді ∠В = 90° – х°. За властивістю суміжних кутів ∠PAR = 180° – x°, ∠RBA = 180° – (90° – х°) = 90° + х°.
За умовою задачі маємо: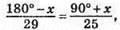 
звідси 4500 – 25x = 26401 – 29x.
54x = 1890; x = 35.
Отже, ∠A = 35°, ∠B = 90° – 35° = 55°.
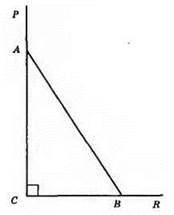
Відповідь: 35°, 55°.
(1 votes, average: 5.00 out of 5)
Loading...