Головна ⇒ 📌ГДЗ з математики ⇒ Задачі на побудову та їх розв’язування

Задачі на побудову та їх розв’язування

Розділ 4. Коло і круг. Геометричні побудови

§ 26. Задачі на побудову та їх розв’язування

674.

Задачі на побудову та їх розвязування

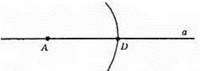
Позначимо на прямій а точку А – початок відрізка AВ. Побудуємо циркулем коло із центром у точці А, радіус якого дорівнює AB. Це коло перетне пряму а у деякій точці D. Очевидно, що АВ =AD. Отже, AD – шуканий відрізок.

675.

Задачі на побудову та їх розвязування

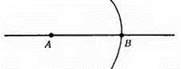
Побудова аналогічна завданню 674.

676.

Задачі на побудову та їх розвязування

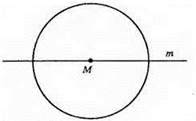
Коло перетне пряму m у двох точках.

677.

Задачі на побудову та їх розвязування

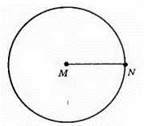
678.

Задачі на побудову та їх розвязування

class=""/>

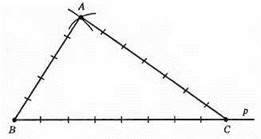
1) За допомогою лінійки проведемо довільну пряму р і позначимо на ній довільну точку В. Відкладемо на прямій р відрізок ВС = 8 см.

2) Розхилом циркуля, що дорівнює 7 см, опишемо дугу із центром у точці С.

3) Розхилом циркуля, що дорівнює 5 см, опишемо дугу кола із центром у точці В. Точка А – точка перетину дуг, проведених з точок В і С.

4) З’єднаємо точки А, В, С відрізками.

?ABC – шуканий.

679.

Задачі на побудову та їх розвязування

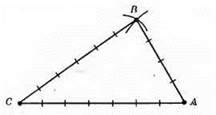
1) Проведемо довільну пряму т. На ній відкладемо відрізок СА = 7 см.

2) Розхилом циркуля, що дорівнює 4 см, опишемо дугу кола із центром у точці А.

3) Розхилом циркуля,

що дорівнює 6 см, опишемо дугу кола із центром у т. С. Точка В – точка перетину дуг, проведених з точок А і С.

4) З’єднаємо точки А, В, С відрізками.

?ABC – шуканий.

680.

Задачі на побудову та їх розвязування

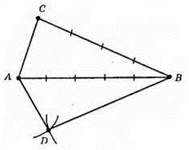
1) Розхилом циркуля, що дорівнює стороні АС трикутника АВС, опишемо дугу кола із центром у т. А.

2) Розхилом циркуля, що дорівнює стороні СВ трикутника ABC, опишемо душу кола із центром у т. В. Точка D – точка перетину дуг.

3) З’єднаємо т. А, D, В.

?ADB – шуканий.

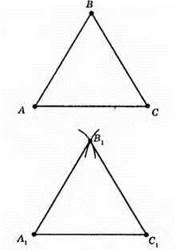
681. 1) Будуємо відрізок А1С1 = АС.

2) Розхилом циркуля, який дорівнює стороні AB? ABC, опишемо дугу кола із центром у точці A1.

3) Розхилом циркуля, що дорівнює стороні ВС? ABC, опишемо дугу кола із центром у точці С1. Точка В – точка перетину дуг.

4) З’єднаємо точки А1, В1, С1 відрізками. Трикутник А1В1С1 – шуканий.

Задачі на побудову та їх розвязування

682.

Задачі на побудову та їх розвязування

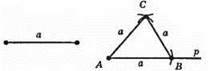
1) За допомогою лінійки проводимо довільну пряму р і позначимо на ній т. А.

2) За допомогою циркуля відкладемо засічкою на прямій р а відрізок AB = а.

3) Розхилом циркуля, що дорівнює а, опишемо дуги кола із центром у т. А і т. В. Точка С – точка перетину дуг.

4) З’єднаємо точки А, В і С відрізками.

?ABC – шуканий.

683.

Задачі на побудову та їх розвязування

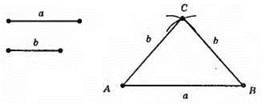
1) Будуємо а.

2) Розхилом циркуля, який дорівнює Ь, проводимо дуги кіл із центрами у т. А і т. В. Точка С – точка перетину дуг.

3) З’єднаємо т. А, В і С відрізками.

?ABC – шуканий.

684.

Задачі на побудову та їх розвязування

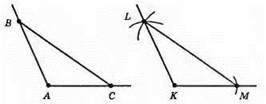
1) Позначимо на сторонах даного кута А точки В іС.

2) Побудуємо? LKM, що дорівнює? ВАС, так щоб LK = BA, LM = ВС, КМ = АС.

3) ∠LKM = ∠BAC – як відповіді кути рівних трикутників.

4) ∠LKM – шуканий.

685.

Задачі на побудову та їх розвязування

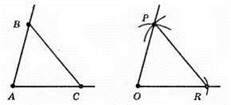
1) Позначимо на сторонах даного кута т. В і т. С.

2) Побудуємо? ОРR, що дорівнює? ABC, так, щоб OP = AB, PR = ВС, OR = AC.

3) ∠POR = ∠BAC – як відповідні кути рівних трикутників.

4) ∠POR – шуканий.

686.

Задачі на побудову та їх розвязування

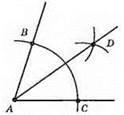
Нехай ∠A = 70°.

1) Проведемо дугу кола довільного радіуса із центром у т. А, яка перетинає сторони кута А в точках В і С.

2) 3 т. В і С опишемо дуги таким самим радіусом у внутрішній області кута до їх перетину. Отримаємо т. D.

3) Проведемо промінь AD.

Промінь AD – шукана бісектриса.

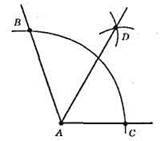
687. Нехай ∠A = 110°.

1) Проведемо дугу кола довільного радіуса із центром у т. А, яка перетинає сторони кута А в точках В і С.

2) 3 точок В і С опишемо дуги таким самим радіусом у внутрішній області кута до їх перетину. Отримаємо т. D.

3) Проведемо промінь AD.

Промінь AD – шукана бісектриса.

Задачі на побудову та їх розвязування

688.

Задачі на побудову та їх розвязування

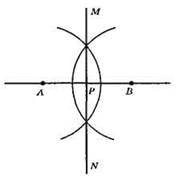
Нехай AB – даний відрізок.

1) 3 т. А радіусом циркуля, більшим за половину відрізка AB опишемо дугу.

2) 3 т. В таким самим радіусом циркуля опишемо дугу до перетину з першою дугою в точках М і N.

3) Через т. М і N проведемо пряму MN, яка перетинає відрізок AB в т. Р.

Р – шукана точка.

689.

Задачі на побудову та їх розвязування

Нехай AB – даний відрізок.

1) 3 т. А радіусом циркуля, більшим за половину відрізка AB опишемо дугу.

2) 3 т. В таким самим радіусом опишемо дугу до перетину з першою дугою в т. М і N.

3) Через т. М і N проведемо пряму MN. Пряма МТ перетинає відрізок AB в т. Р.

Р – середина AB.

690.

Задачі на побудову та їх розвязування

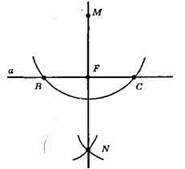
Нехай т. М не належить прямій а.

1) 3 т. М довільним радіусом, більшим за відстань від т. М до прямої а, проведемо дугу, яка перетинає пряму а в точках B і С.

2) Із точок В і С тим самим радіусом циркуля опишемо дуги до їхнього перетину в точці N по інший бік від точки М.

3) Проведемо пряму MN.

Пряма MN – шукана пряма.

691.

Задачі на побудову та їх розвязування

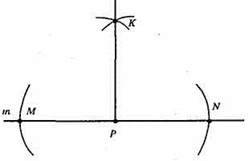
Нехай Р є m.

1) На даній прямій то довільним радіусом циркуля відкладемо від т. Р два рівних відрізка РМ і PN.

2) Із точок М i N радіусом, що дорівнює MN, опишемо дуги до їхнього перетину. Отримаємо т. К.

3) Проведемо пряму KP.

KP – шукана пряма.

692.

Задачі на побудову та їх розвязування

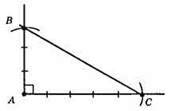
Щоб побудувати прямокутний трикутник за двома катетами, слід побудувати прямий кут і на його сторонах відкласти відрізки, що дорівнюють катетам: АВ = 3 см, АС = 5 см.

?ABC – шуканий.

693.

Задачі на побудову та їх розвязування

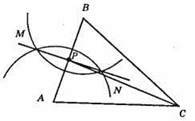
1) 3 точки А радіусом циркуля, більшим за половину відрізка АВ, опишемо дугу.

2) 3 точки В таким самим радіусом проведемо дугу до перетину з першою дугою в точках М і N. Через т. М і N проведемо пряму, яка перетинає AB в точці Р. Р – середина сторони АВ.

Проведемо пряму CP. СР – шукана медіана.

694.

Задачі на побудову та їх розвязування

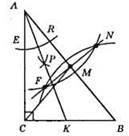
1) 3 точок А і С проводимо кола довільного радіусу, які перетинаються в точках N i F.

2) Знаходимо точку М перетину прямої FN та сторони АВ.

3) СМ – шукана медіана.

4) Проведемо дугу кола довільного радіуса із центром в т. А, яка перетинає сторони кута А в точках E i R.

5) 3 точок E i R опишемо дуги таким самим радіусом у внутрішній області кута до їхнього перетину. Отримаємо т. Р.

6) АР, а отже, і АК – бісектриса кута А.

695.

Задачі на побудову та їх розвязування

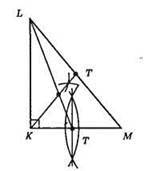
Побудова аналогічна завданню 694.

696.

Задачі на побудову та їх розвязування

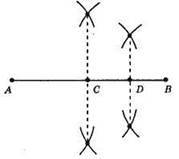
1) Ділимо відрізок АВ навпіл.

2) Ділимо відрізок СВ навпіл.

3) Відрізок AD = 3/4AB.

697.

Задачі на побудову та їх розвязування

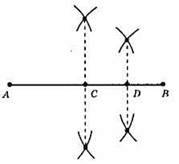
1) Ділимо відрізок АВ навпіл.

2) Ділимо відрізок CD навпіл.

3) DB = 1/4BA.

698.

Задачі на побудову та їх розвязування

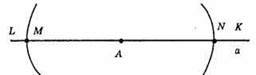
1) На прямій а існує дві точки M i N, віддалені від т. А на відстань 4 см.

2) На прямій а існує безліч точок, віддалених від даної точки А на відстань більше 4 см, це промені NK і ML без початків.

3) На прямій а існує безліч точок, віддалених від даної точки А на відстань меншу ніж 4 см, це відрізок MN без його кінців.

699.

Задачі на побудову та їх розвязування

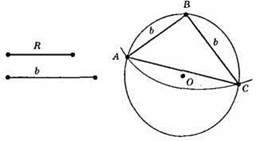
1) Будуємо коло з центром у т. О і з радіусом R.

2) 3 довільної точки В кола будуємо коло радіуса b, яке перетинає побудоване коло в точках А і С.

3) ?ABC – шуканий.

700.

Задачі на побудову та їх розвязування

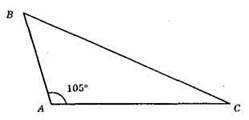
1) Будуємо кут ∠A = 105°.

2) На сторонах кута відкладаємо відрізки AB = 3 см, АС = 5 см.

3) ?ABC – шуканий.

701.

Задачі на побудову та їх розвязування

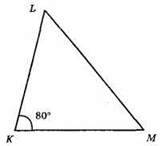
1) Будуємо кут ∠K = 80°.

2) На сторонах кута відкладаємо відрізки KL = 6 см, КМ = 4 см.

3) ?KLM – шуканий.

702.

Задачі на побудову та їх розвязування

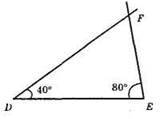
1) Побудуємо кут ∠D = 40°.

2) На одній стороні кута відкладаємо відрізок DE = 6 см.

3) Будуємо ∠E = 80°.

4) Точка F – точка перетину сторін кутів D i E.

5) ADEF – шуканий.

703.

Задачі на побудову та їх розвязування

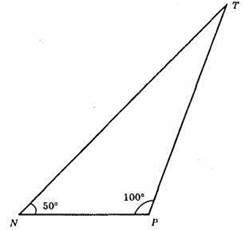
1) Будуємо ∠N = 50°.

2) На одній стороні відкладемо відрізок NP = 4 см.

3) Будуємо ∠P = 100°.

4) ?NPT – шуканий.

704.

Задачі на побудову та їх розвязування

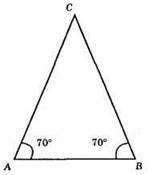
1) Будуємо AB = 4 см.

2) Будуємо ∠ВАС = 70°.

3) Будуємо ∠ВАС = 70°.

4) ?ABC – шуканий.

705.

Задачі на побудову та їх розвязування

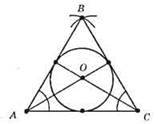
1) Будуємо відрізок АС = 5 см, який дорівнює стороні рівностороннього трикутника.

2) За допомогою циркуля проведемо дуги з центром у точках А і С, радіусом, який дорівнює АС.

3) Оскільки центр вписаного кола є точкою перетину бісектрис, будуємо бісектриси кутів А і С. О – точка перетину бісектрис – центр вписаного кола.

706.

Задачі на побудову та їх розвязування

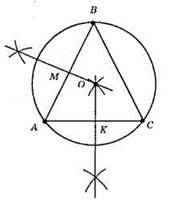
?ABC – довільний трикутник. Оскільки центром описаного кола навколо трикутника є точка перетину серединних перпендикулярів, то побудуємо серединні перпендикуляри до сторін AB і АС.

1) Знайдемо середини відрізків AB і АС. Точки М і К – середини відрізків відповідно AB і АС.

2) Побудуємо перпендикуляри до сторін трикутника АВ і АС, які проходять через точки М і К відповідно, т. О – точка перетину серединних перпендикулярів – центр описаного кола.

707.

Задачі на побудову та їх розвязування

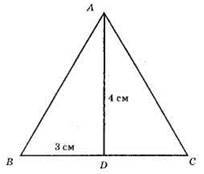
1) Будуємо прямокутний трикутник ABD за катетом BD = 6/2 = 3 (см) і AD = 4 см.

2) На промені BD від точки D відкладемо DC = 3 см.

3) ?АBС – шуканий.

Оскільки AD – висота і медіана трикутника ABC, то трикутник ABC – рівнобедрений.

708.

Задачі на побудову та їх розвязування

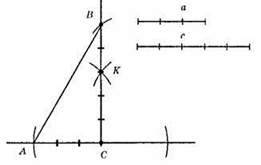
1) Із точки С відкладемо рівні відрізки АС = а.

2) Із отриманих точок проводимо кола більшого радіуса, які перетнуться в точці К.

3) Через точку перетину кіл і точку С проводимо пряму СК.

4) Із точки А проводимо коло радіуса с, яке перетне пряму СК в точці В.

5) ?АВС шуканий, оскільки ВС ⊥ АС, бо ВС – серединний перпендикуляр, АС = а, ВА = с.

709. 1) Із точки С на прямій відкладаємо рівні відрізки СА = а.

2) Із отриманих точок проводимо кола більшого радіуса, які перетнуться в точці К.

Задачі на побудову та їх розвязування

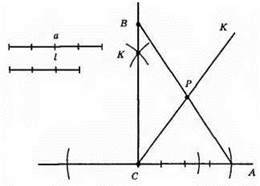
3) Через точку перетину кіл і точку С проводимо пряму КС.

4) Будуємо бісектрису кута С – СК.

5) На прямій СК відкладаємо бісектрису трикутника, яка дорівнює l. Отримаємо т. Р.

6) Через точки A і Р проводимо пряму до перетину з прямою СК, отримаємо точку В.

7) ?ABC – прямокутний шуканий трикутник, оскільки СК – серединний перпендикуляр.

710.

Задачі на побудову та їх розвязування

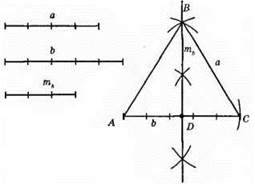
1) Будуємо? ABD за трьома сторонами: AB = a, BD = mb, AD = b/2.

2) Відкладемо на промені AD відрізок АС = b.

3) Проводимо відрізок ВС.

4) ?ABC – шуканий.

711. ОА – радіус кола. Оскільки дотична перпендикулярна до радіуса, то побудуємо пряму, перпендикулярну до ОА.

1) На прямій О А довільним радіусом циркуля відкладемо від т. А два рівні від, різки AB і АС.

Задачі на побудову та їх розвязування

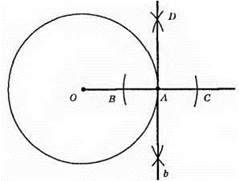
2) Із точок В і С радіусом, який дорівнює ВС, опишемо дуги до їхнього перетину. Отримаємо т. D.

3) Проведемо пряму b через т. D і А, яка перпендикулярна до ОА. Отже, b – дотична до кола.

712.

Задачі на побудову та їх розвязування

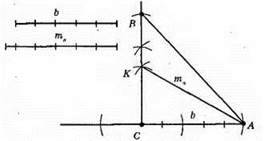
1) Будуємо прямокутний трикутник за катетом b і гіпотенузою, яка дорівнює mа.

2) Оскільки mа – гіпотенуза прямокутного? ABC, то відкладемо на прямій СК відрізок КВ = СК.

3) ?АВС – шуканий.

713.

Задачі на побудову та їх розвязування

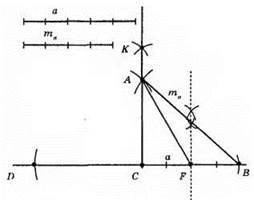
1) Із т. С на прямій відкладемо рівні відрізки СВ = а.

2) Із отриманих точок D і В проводимо кола більшого радіуса, які перетнуться в точці К.

3) Через точку К і точку С проводимо пряму KС.

4) Розділимо відрізок СВ на дві рівні частини. Т. F – середина відрізка.

5) 3 точки F проведемо кола радіуса та до перетину з прямою КС. Отримаємо т. А.

6) З’єднаємо т. А з т. В.

?ABC – шуканий.

714.

Задачі на побудову та їх розвязування

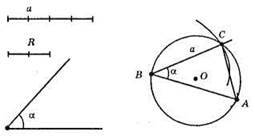
1) Будуємо коло з центром у точці О і з радіусом R.

2) 3 довільної точки В кола будуємо коло з радіусом а.

3) Від променя ВС відкладемо кут СВА = α, сторона якого перетне коло у точці А.

4) ?АВС – шуканий.

715.

Задачі на побудову та їх розвязування

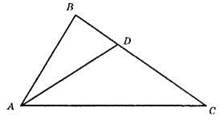
1) Будуємо? ADC за двома сторонами AD = l, АС = b і кутом між ними ∠DAC = α/2.

2) Будуємо ∠BAD = α/2, точка В – точка перетину сторони AB кута BAD і продовження сторони DC.

716.

Задачі на побудову та їх розвязування

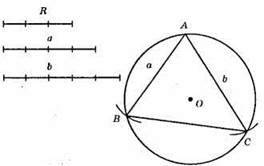
1) Будуємо коло з центром у т. О і радіусом R.

2) 3 довільної точки А будуємо коло з радіусом а, яке перетне побудоване коло в точці В.

3) 3 цієї ж точки А будуємо коло з радіусом 6, яке перетне побудоване коло в точці С.

4) ?АВС – шуканий.

717.

Задачі на побудову та їх розвязування

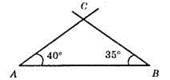
1) Будуємо відрізок AB = 4 см.

2) Від т. А відкладаємо ∠A = 40°.

3) Знайдемо ∠В. ∠В = 180° – 40° – 105° = 35°.

4) Від т. В відкладаємо кут 35°.

5) ?ABC – шуканий.

718.

Задачі на побудову та їх розвязування

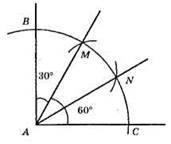
1) За допомогою косинця будуємо прямий кут. А.

2) Довільним радіусом описуємо коло з центром в т. А до перетину сторін кута в точках В і С.

3) 3 точок В і С, як з центрів проводимо дві дуги того ж радіуса до перетину з побудованим колом в точках М і N.

4) ∠BAM = 30°, ∠MAC = 60°.

719.

Задачі на побудову та їх розвязування

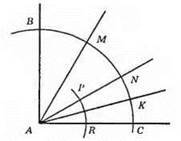
1) Спочатку будуємо кут NAC, який дорівнює 30° (як в попередньому завданні).

2) Будуємо бісектрису ∠NAC. Проводимо дугу кола довільного радіуса із центром у т. А, яка перетинає сторони кута NAC в точках Р і R.

3) 3 точок Р і R опишемо дуги у внутрішній області кута таким самим радіусом до їхнього перетину, отримаємо точку К.

4) Проведемо промінь AK. АК – бісектриса. Отже, ∠NAK = ∠KAC = 15°.

720. I.

Задачі на побудову та їх розвязування

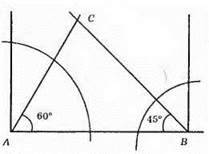
1) Будуємо прямий кут А за допомогою косинця.

2) Від точки А на стороні кута відкладаємо 5 см, отримаємо AВ = 5 см.

3) За допомогою циркуля будуємо кут А = 60°.

4) За допомогою циркуля будуємо кут В = 45°.

5) ?ABC – шуканий.

II. Нехай т. В належить прямій а.

Задачі на побудову та їх розвязування

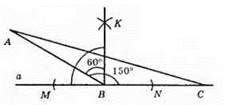
1) На дані й прямій а довільним радіусом відкладемо від т. В два рівних відрізка ВМ і BN.

2) Із точок М і N радіусом, що дорівнює MN опишемо дуги до їхнього перетину, отримаємо точку К.

3) Проведемо пряму KB. КВ ⊥ МС.

4) Побудуємо кут, який дорівнює 60°. Для цього поділимо кут КВМ на три рівних кути (див. завдання 718). Отримаємо: ∠ABK = 60°, тоді ∠ABC = 60° + 90° = 150°.

5) Відкладемо на сторонах кута ВА = ВС = 4 см.

6) З’єднаємо точки А і С. Отримаємо? АДС – шуканий.

721. I.

Задачі на побудову та їх розвязування

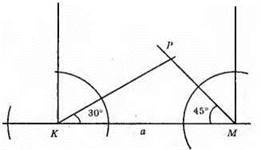
1) На прямій а відкладемо КМ = 4 см.

2) 3 точок К і М проведемо прямі перпендикулярні до прямої а.

3) Побудуємо кут, який дорівнює 30° з вершиною в точці К (див. завдання 718).

4) Побудуємо кут, який дорівнює 45° з вершиною в т. М (див. завдання 720.1)).

5) ?КРМ – шуканий.

II.

Задачі на побудову та їх розвязування

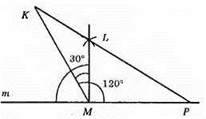
1) На прямій m позначимо т. М.

2) Проведемо LM ⊥ m.

3) Побудуємо кут, який дорівнює 30°, тоді ∠KMP = ∠KML + ∠LMP = 30° + 90° = 120°.

4) На сторонах кута КМР відкладемо відрізки КМ = МР = 5 см.

5) ?КМР – шуканий.

722. Знайдемо кут при основі трикутника.

Задачі на побудову та їх розвязування

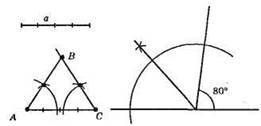
1) Побудуємо кут, який дорівнює 80° і суміжний з ним кут.

2) Поділимо суміжний кут навпіл, це і буде кут при основі трикутника. Будуємо трикутник за стороною і двома прилеглими кутами. Отже, ?ABC – шуканий.

723. Побудова аналогічна завданню 722.

724.

Задачі на побудову та їх розвязування

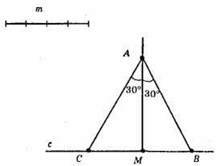
Оскільки в рівносторонньому трикутнику медіана є і бісектрисою, то кут при вершині трикутника ділиться на два рівних кути кожен по 30°.

Рис. 1) Будуємо медіану AM.

2) 3 т. А відкладаємо кути 30° по різні боки від медіани.

3) Через т. М проводимо пряму с ⊥ АМ.

4) ?ABC – шуканий.

725.

Задачі на побудову та їх розвязування

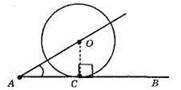
∠OAC = 30°, ОС ⊥ AB (оскільки AB – дотична, ОС – радіус кола), ОС = 5 см. Оскільки? АОС – прямокутний (∠C = 90°) з кутом 30°, то АО = 2ОС = 2 x 5 = 10 см.

Відповідь: 10 см.

726.

Задачі на побудову та їх розвязування

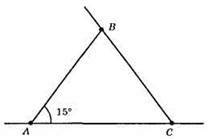
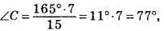
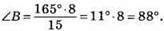
Hexaй ∠A = 15°, ∠C : ∠B = 7 : 8. ∠B + ∠C = 180° – 15° = 165°, тоді Задачі на побудову та їх розвязування Задачі на побудову та їх розвязування

Оскільки зовнішній кут при вершині трикутника суміжний з внутрішнім кутом і вони в сумі дорівнюють 180°, то зовнішній кут, тим менше, чим більше внутрішній кут, суміжний з ним.

Найбільший кут трикутника дорівнює 88°, отже, найменший зовнішній кут дорівнює 180° – 88° = 92°.

Відповідь: 92°.

727.

Задачі на побудову та їх розвязування

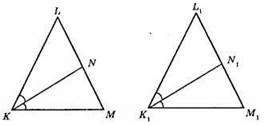
Нехай? KLM = ?K1L1M1, KN, K1N1 – бісектриси. Оскільки? KLM = ?K1L1M1, то ∠M = ∠M1, KM = K1M1, ∠NKM = ∠N1K1M1 – як половини рівних кутів. Тоді? NKM = ?N1K1M1 – за стороною і двома прилеглими кутами. Отже, KN = K1N1.

728.

Задачі на побудову та їх розвязування

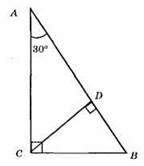
?ABC – прямокутний, ∠A = 30°, AB = 60 CM. CD ⊥ AB.

∠B = 90° – ∠A = 90° – 30° = 60°.

З прямокутного? СDB: ∠DCB = 90° – ∠B = 90° – 60° = 30°.

З? АВС: CB = 1/2AB = 1/2 • 60 = 30 (CM).

З? CDB: DB = 1/2CB = 1/2 • 30 = 15 (см).

AD = AB – DB = 60 – 15 = 45 (см).

Відповідь: 15 см, 45 см.

729.

Задачі на побудову та їх розвязування

Відповідь: 40.


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Найпростіші задачі па побудову Розділ 1. Найпростіші геометричні фігури та їх властивості § 18. Найпростіші задачі па побудову 708. Щоб побудувати трикутник, що дорівнює трикутнику ABC, треба провести три кола радіусами 5 см, 6 см і 9 см. 709. 710. 1) AС = 5 см; 2) AС = 0,35 дм; 3) AС = 43 мм. 711. 1) Будуємо відрізок […]...

  2. Складніші задачі на побудову Розділ 1. Найпростіші геометричні фігури та їх властивості § 19. Складніші задачі на побудову 736. Так. 737. Мал. 401. X належить бісектрисі кута В та колу. Мал. 402. X належить бісектрисі кута В та серединному перпендикуляру ОХ до відрізка ВС. Мал. 403. X належить серединному перпендикуляру ВО до відрізка АС та колу. 738. 1) Спочатку […]...

  3. Вправи для повторення розділу 4 Розділ 4. Коло і круг. Геометричні побудови Вправи для повторення розділу 4 До § 21. 756. AB – діаметр, ОС – радіус. AD – хорда. 757. 1) Коло з променем ОК має одну спільну точку. 2) Коло з прямою ОК має дві спільні точки. 758. ?АОВ = ?ВОС за двома сторонами і кутом між ними […]...

  4. ЗАДАЧІ НА ПОБУДОВУ РОЗДІЛ 4 КОЛО І КРУГ. ГЕОМЕТРИЧНІ ПОБУДОВИ & 21. ЗАДАЧІ НА ПОБУДОВУ З геометричними побудовами мають справу різні фахівці. Геометричні побудови виконують креслярі, архітектори, конструктори, топографи, геодезисти, штурмани. Геометричні фігури також будують: слюсар – на жерсті, столяр – на дошці, кравець – на тканині, садівник – на землі. У задачі на побудову вимагається побудувати геометричну […]...

  5. ГЕОМЕТРИЧНІ ПОБУДОВИ РОЗДІЛ 4 КОЛО І КРУГ. ГЕОМЕТРИЧНІ ПОБУДОВИ & 18. ГЕОМЕТРИЧНІ ПОБУДОВИ Користуючись лінійкою1 і циркулем, можна виконувати багато геометричних побудову тобто креслити геометричні фігури. Розглянемо спочатку, як виконувати найпростіші геометричні побудови. ЗАДАЧА 1 Побудуйте трикутник із даними сторонами. РОЗВ’ЯЗАННЯ. Нехай дано три відрізки: а, b і с (мал. 224). Треба побудувати трикутник, сторони якого дорівнювали […]...

  6. Вправи 625-682 625. Геометричним місцем центрів кіл радіуса R, що проходить через дану точку А, є коло із центром в точці А і радіусом R. 626. Геометричним місцем центрів кіл, що дотикаються до сторін даного нерозгорнутого кута, є бісектриса даного кута без його вершини О. ОК – бісектриса. 627. Геометричним місцем точок С, які є вершинами трикутників […]...

  7. Вправи 575-624 575. АВ і АС дотикаються до кола з центром О у точках В і С. ∠CBO = 40°. ?АBО – прямокутний, OB ⊥ AB (OB – радіус, проведений в точку дотику). ?АСО – прямокутний (ОС – радіус, проведений в точку дотику). ∠ABO = 90°; ∠ACO = 90°; ?ВОС – рівнобедрений, OB = ОС; ∠OBC = […]...

  8. Задачі на побудову Урок № 46 Тема. Задачі на побудову Мета: домогтися засвоєння учнями схеми розв’язання задач на побудову [метод допоміжного трикутника]; сформувати вміння виконувати дії за загальною схемою розв’язання задач на побудову, що приведуть до побудови шуканої фігури. Тип уроку: застосування вмінь та навичок. Наочність і обладнання: набір демонстраційного креслярського приладдя; таблиця “Загальна схема розв’язання задач на […]...

  9. Дотична до кола, її властивості Розділ 4. Коло і круг. Геометричні побудови § 22. Дотична до кола, її властивості 607. Проведемо радіус ОР, а потім за допомогою косинця побудуємо пряму m, перпендикулярну до радіуса. За теоремою 2 пряма m є дотичною до кола. 608. Проведемо радіус ОМ, а потім за допомогою косинця побудуємо пряму n, перпендикулярну до радіуса. За теоремою […]...

  10. ВІДПОВІДІ І ВКАЗІВКИ ВІДПОВІДІ І ВКАЗІВКИ 7. АB. 11. Так. 12. Не належить. 13. КР, РТ, КТ, РК, TP, ТК. 16. 4. 19. Можна. 21. 6. Hа 16,17 або 18 частин. 28. 20,5 см. 29. 8 см. 31.10 дм. 33. 1) 2 см; 6 дм; 20 км. 34. 21 см. 42. Так. 44. а) 5,9 см. 45. а) […]...

  11. Коло Геометрія Основні властивості найпростіших геометричних фігур Коло Колом називається фігура, яка складається з усіх точок площини, рівновіддалених від даної точки. Ця точка називається Цент­ром кола. Відстань від точок кола до його центра називається Радіусом кола. Радіусом також називається будь-який відрізок, що сполучає точку кола з його центром. Відрізок, що сполучає дві точки кола, називається Хордою. […]...

  12. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої Розділ 2. Взаємне розміщення прямих па площині § 7. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої 128. m ⊥ n, MN ⊥ АВ. 129. KA ⊥ c, ВМ ⊥ с. 130. ВL ⊥ a. MВ ⊥ a. 131. 1) Відрізки AB і MN перпендикулярні, оскільки вони лежать на перпендикулярних прямих a і b. 2) […]...

  13. Описані і вписані кола Розділ 1. Найпростіші геометричні фігури та їх властивості § 17. Описані і вписані кола 671. Коло, описане навколо трикутника, зображено на мал. 372. 672. Коло, вписане у трикутник, зображено на мал. 375. 673. Центр кола, описаного навколо гострокутного трикутника, лежить всередині трикутника. Центр кола, описаного навколо прямокутного трикутника, лежить на середині гіпотенузи. Центр кола, описаного […]...

  14. Відстань від точки до прямої. Розв’язування задач на застосування теореми про три перпендикуляри Урок 35 Тема. Відстань від точки до прямої. Розв’язування задач на застосування теореми про три перпендикуляри Мета уроку: формування вмінь учнів застосувати теорему про три перпендикуляри до розв’язування задач, знаходження відстані від точки до прямої. Обладнання: стереометричний набір. Хід уроку І. Перевірка домашнього завдання. 1. Два учні відтворюють на дошці розв’язування задач № 13, 41. […]...

  15. Задачі за готовими рисунками ДОДАТКИ Задачі за готовими рисунками 1 О – центр кола. Знайдіть АС 2 NB – діаметр, NB = 10, ОК = 4. Знайдіть АВ 3 О – центр кола. Знайдіть МО 4 Знайдіть АЕ 5 Знайдіть ВС 6 О – центр кола, АВ дотична, ОА = 25. Знайдіть АВ 7 О – центр кола. АВ […]...

  16. Круг. Площа круга. Круговий сектор Розділ 3 Відношення і пропорції §30. Круг. Площа круга. Круговий сектор Коло ділить площину на дві частини. Частина площини, яка лежить усередині кола, разом із колом утворюють круг (мал. 24). Центр, радіус і діаметр кола одночасно є центром, радіусом і діаметром круга. Відстань від центра до будь-якої точки круга не перевищує радіуса круга. Як знайти […]...

  17. Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих Розділ 2. Взаємне розміщення прямих па площині § 9. Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих 170. Рис. 119: ∠1 і ∠2 – внутрішні різносторонні кути. Рис. 120: ∠1 і ∠2 – відповідні кути. Рис,121: ∠1 i ∠2 – внутрішні різносторонні кути. 171. Внутрішні односторонні кути: ∠ANM і ∠NMB, ∠CNM і ∠NMD. […]...

  18. Кути та їх міри Урок № 18. Тема. Кути та їх міри Мета. Засвоїти поняття кута градусної міри кута, променя, що проходить між сторонами кута; вимірювати кути; записувати кути з малюнка; застосовувати властивості кутів до розв’язання задач, розвивати увагу та допитливість, виховувати інтерес до математики. Обладнання: кодоскоп Хід уроку І. Організація класу ІІ. Перевірка домашнього завдання. Двоє учнів розв’язують […]...

  19. Метод координат. Рівняння сфери, площини, прямої Завдання 2 1. 1) Рівняння сфери, усі точки якої рівновіддалені від початку координат на 1 од. має вигляд х2 + у2 + z2= 1. 2) Оскільки центр сфери – початок координат і вона перетинає ось Оz у точці (0; 0; 1), то вона має радіус 1, а значить, її рівняння; х2 + у2 + z2 […]...

  20. Пропорційність відрізків хорд і січних кола Геометрія Кути, пов’язані з колом Пропорційність відрізків хорд і січних кола Теорема 1. Якщо хорди AB і CD кола перетинаються в точці S, то (рисунок 1). Теорема 2. Якщо з точки P до кола проведені дві січні, що перетинають коло відповідно в точках A, B, C, D, то (рисунок 2). Тобто добуток січної, проведеної до […]...

  21. Вправи для повторення до розділу 2 Розділ 2. Взаємне розміщення прямих па площині Вправи для повторення до розділу 2 До § 5. 226. На рис. 184 суміжні кути ∠2 і ∠3. на рис. 185 суміжні кути ∠1 і ∠4 та ∠2 i ∠3. На рис. 186 суміжні кути ∠1 і ∠2 та ∠3 i ∠4. 227. 1) Так, можна. Треба побудувати […]...

  22. Перпендикулярні прямі Розділ 4 Раціональні числа і дії мідними §51. Перпендикулярні прямі Дві прямі, що мають одну спільну точку, називають прямими, що перетинаються. Їх спільну точку називають точкою перетину. На малюнку 89 прямі а і b перетинаються, М – точка їх перетину. Дві прямі, перетинаючись, окрім розгорнутих, утворюють чотири кути зі спільною вершиною, градусна міра яких менша […]...

  23. Кут між площинами Геометрія Стереометрія Кут між площинами Кут між паралельними площинами вважається таким, що дорівнює . Нехай дані площини перетинаються (див. рисунок). Проведемо площину, перпендикулярну до прямої їх перетину. Ця площина перетинає дані площини по двох прямих. Кут між цими прямими називається Кутом між даними площинами. Означений таким чином кут між площинами не залежить від вибору січної […]...

  24. Вправи 525-574 525. АВ = CD; AO : OB = CO : OD; ?СОВ = ?AOD (за двома сторонами і кутом МІНІ ними). З рівності трикутників маємо: BC = AD. ?ВСА = ?DAC. 1) АС – спільна сторона; 2) AB = CD; 3) BC = DA; ∠MCA = ∠MAC; отже, ∠A = ∠C; ?CMА – рівнобедрений; МС […]...

  25. Коло. Довжина кола Розділ 3 Відношення і пропорції §29. Коло. Довжина кола Дуже давно люди винайшли колесо та побачили його корисні в побуті властивості. Геометричними фігурами, які дають уявлення про колесо, є коло і круг. На малюнку 15 зображено креслярський інструмент – циркуль. На одній його ніжці – вістря, а на другій – грифель. Якщо поставити ніжку з […]...

  26. Тригранні кути 562. Нехай дано тригранний кут, усі плоскі кути якого прямі. Лінійний кут кожного тригранного кута прямий, отже всі його двогранні кути прямі. 563. Якщо всі двогранні кути тригранного кута рівні, то кожний з них більше за 60°, оскільки ∠1 + ∠2 + ∠3 > 180°; ∠Α = ∠1 – ∠2 = ∠3, то 3∠A > […]...

  27. Властивості сфери і кулі 1. Відстань, яка б відділяла мене від мого антипода дорівнювала б Двом радіусам Землі. Відповідь: 2R Землі. 2. Нехай АО – радіус Землі, ОА = 6400 км, О1А – радіус Полярного кола Землі. Координати Полярного кола Землі 66°31′ п. ш. ∠АОВ = 66°31′; ∠О1ОА = 90° – 67° = 23°. З ΔO1ОA: Ο1Α = ОА […]...

  28. Розв’язування задач на знаходження кутів у просторі Урок 57 Тема. Розв’язування задач на знаходження кутів у просторі Мета уроку: формування вмінь учнів знаходити кути у просторі. Обладнання: стереометричний набір, модель куба. Хід уроку 1. Два учні відтворюють розв’язування задач № 48 (2) 49 (1) на дошці. 2. Фронтальне опитування. 1) Сформулюйте теорему про площу ортогональної проекції много­кутника. 2) Знайдіть площу ортогональної проекції […]...

  29. Рівняння сфери, площини і прямої 79. (x – 1)2 + у2 + (2 – 4)2 = 25. 80. A(10; 0; 0), В(0; 10; 0), С(0; 0; 10). 81. M(3; 2; -1) не належить сфері. X2+ у2 + z2 – 2х + 4у – 6z – 2 = 0, бо 32 + 22 + (-1)2 – 2 × 3 + 4 […]...

  30. Точка та прямі § 1. Найпростіші геометричні фігури та їхні властивості 1. Точка та прямі Практичні завдання 1. 2. Прямі ME, МК, ЕК, EM, КМ, КЕ. 3. Точка С належить прямій а, точка С належить прямій b. 4. Утворилося три прямих. 5. 6. Можна отримати три або одну точку перетину. 7. 1) 2) 3) Вправи 8. 1) Прямій […]...

  31. Перетворення подібності та його властивості. Гомотетія УРОК № 38 Тема. Перетворення подібності та його властивості. Гомотетія Мета уроку: формування понять перетворення подібності й гомотетії; вивчення властивостей перетворення подібності; формування вмінь застосовувати вивчені властивості й означення до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення подібності” [13]. Вимоги до рівня підготовки учнів: описують перетворення подібності й гомотетію; будують фігури, у […]...

  32. Рівняння кола УРОК № 26 Тема. Рівняння кола Мета уроку: виведення рівняння кола. Формування вмінь учнів використовувати рівняння кола до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати і вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють рівняння кола. Розпізнають рівняння кола. Хід уроку I. Перевірка домашнього завдання Перевірити наявність […]...

  33. Теорема Гульдіна 1379. У трикутнику ABC AB = ВС, AC = a, BK + AC, BK = h. Центром мас трикутника ABC є точка O – точка перетину медіан трикутника ABC: Тоді і Відповідь: 1380. ABCD – ромб, AB = a, ∠BAD = a, BD? I. SABCD = AB2 sin∠BAD = а2 sin α. Центром мас ромба […]...

  34. Розв’язування задач на знаходження відстані між мимобіжними прямими Урок 41 Тема. Розв’язування задач на знаходження відстані між мимобіжними прямими Мета уроку: формування вмінь учнів у знаходженні відстані між двома мимобіжними прямими. Обладнання: стереометричний набір, моделі куба і прямокутного паралелепіпеда. Хід уроку 1. Фронтальна бесіда за контрольними запитаннями № 13-15 та пе­ревірка правильності розв’язання домашньої задачі. 2. Математичний диктант. Дано зображення куба: варіант 1 […]...

  35. Перпендикуляр до прямої Урок № 19 Тема. Перпендикуляр до прямої Мета: домогтися розуміння учнями змісту теореми про існування та єдиність прямої, що проходить через будь-яку точку площини перпендикулярної даній; понять: “перпендикуляр, проведений з точки до прямої”, “відстані від точки до прямої”. Сформувати вміння: – відтворювати зміст зазначеної теореми та застосовувати її під час розв’язування задач; – на рисунку […]...

  36. Заключний урок з теми “Геометричні побудови” Урок № 51 Тема. Заключний урок з теми “Геометричні побудови” Мета: систематизувати та узагальнити знання учнів, набуті в ході вивчення теми “Геометричні побудови”. Систематизувати та узагальнити вміння учнів розв’язувати задачі: – на застосування означення та властивостей кола і його елементів; – на побудову за допомогою циркуля та лінійки; – на метод застосування означення та властивостей […]...

  37. Описане та вписане коло трикутника § 3. Паралельні прямі. Сума кутів трикутника § 20. Описане та вписане коло трикутника 540. 1) Різносторонній гострокутний трикутник. 2) Прямокутний трикутник. 3) Тупокутний трикутник. 541. 1) Рівнобедрений гострокутний трикутник. 2) Рівнобедрений тупокутний трикутник. 542. 543. 544. Вправи 545. Медіана BD рівнобедреного трикутника ABC є в той же час і серединним перпендикуляром до сторони АС […]...

  38. Існування площини, яка проходить через дану пряму і дану точку УРОК 2 Тема. Існування площини, яка проходить через дану пряму і дану точку Мета уроку: вивчення теореми про існування площини, яка проходить через дану пряму і дану точку, що не лежить на прямій. Обладнання: стереометричний набір. Хід уроку І. Перевірка домашнього завдання 1. Фронтальна бесіда за контрольними запитаннями № 1, 2 §1 із підручника з […]...

  39. Зображення просторових фігур на площині Геометрія Стереометрія Зображення просторових фігур на площині Для зображення просторових фігур на площині, як правило, користуються Паралельним проектуванням. Беремо довільну пряму h, яка перетинає площину рисунка , проводимо через довільну точку A фігури пряму, паралельну h. Точка перетину цієї прямої з площиною рисунка буде зображенням точки A. Побудувавши таким чином зображення кожної точки фігури, дістанемо […]...

  40. КОЛО, КРУГ ТА ЇХ ЕЛЕМЕНТИ. ЦЕНТР КОЛА (круга), РАДІУС, ДІАМЕТР. ПОБУДОВА КОЛА. РОЗВ’ЯЗУВАННЯ ВПРАВ І ЗАДАЧ НА ВИВЧЕНІ ВИПАДКИ АРИФМЕТИЧНИХ ДІЙ АРИФМЕТИЧНІ ДІЇ МНОЖЕННЯ ТА ДІЛЕННЯ (продовження) Урок 68. КОЛО, КРУГ ТА ЇХ ЕЛЕМЕНТИ. ЦЕНТР КОЛА (круга), РАДІУС, ДІАМЕТР. ПОБУДОВА КОЛА. РОЗВ’ЯЗУВАННЯ ВПРАВ І ЗАДАЧ НА ВИВЧЕНІ ВИПАДКИ АРИФМЕТИЧНИХ ДІЙ Мета: ознайомити учнів із кругом і колом; навчати відрізняти круг і коло; вчити працювати з циркулем; формувати вміння розв’язувати приклади і задачі на вивчені випадки арифметичних […]...

Ви зараз читаєте: Задачі на побудову та їх розв’язування
«
»