Задачі підвищеної складності
До § 1. Цілі вирази
1102. а) + 1 – 2 + 3 + 4 + 5 – 6 + 7 – 8 – 9 + 10 = 5;
Б) * 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * 10 = 0, виразити неможливо;
В) * 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * 10 = 60. Замість * поставити “+” або “-” неможливо, щоб отримати 60, бо якщо поставити всі “+”, то одержана сума дорівнює лише 55.
1103. n(n + 1) + (n + 2)(n + 3) = n2 + n + n2 + 2n + 3n + 6 = 2n2 + 6n + 6 = 2(n2 + 3n + 3) – число парне, більше, ніж 2, а тому є складеним числом.
1104. а2 + 2аb + 2а – b + 4.
При а = 2 вираз дорівнює 0, тому 4 + 4b + 4 – b + 4 = 0; 3b = -12; b = -4.
При а = 2 і b = -4 значення виразу а2 + аb + b2 = 22 + 2 • (-4) + (-4)2 = 4 – 8 + 16 = 12.
1105.
А) 10m + 9n = 7m + 7n + 3m + 2n = 7(m + n) + (3m + 2n) – ділиться на 7, бо 7(m + n) ділиться на 7 і 3m + 2n ділиться на 7;
Б) 4m + 5n = 7m + 7n – 3m – 2n = 7(m + n) – (3m + 2n) – ділиться на 7, бо 7(m + n) ділиться на 7 і (3m + 2n) ділиться на 7;
В) m + 3n = 7m + 7n – 6m – 4n = 7(m + n) – 2(3m + 2n) – ділиться на 7, бо 7(mг + n) ділиться на 7 і (3m + 2n) ділиться на 7.
1106. Якщо 5m – n ділиться на 8 і 3m + 4n ділиться на 8, то 5m – n + 3m + 4n ділиться на 8. Тобто 8m + 3n – ділиться на 8.
8m ділиться на 8, тому 3n ділиться на 8, отже, n ділиться на 8.
5m – n – ділиться на 8.
N – ділиться на 8, тому 5m ділиться на 8. Отже, m ділиться на 8.
1107. Нехай а і b – дані цілі числа,
А : 7 = k (ост. с); а = 7k + с;
B : 7 = n (ост. с); b – 7n + с.
А – b = 7k + с – (7n + с) = 7k – 7n = 7(k – n) ділиться на 7.
1109. У двох кошиках повинно бути не більше, ніж 140 яєць, бо один кошик поміщає не більше 70 яєць.
Спільні кратні 2; 3; 4; 5; 6: 60; 120; 180; 240; …
Тоді, якщо при розкладанні яєць по 2; 3; 4; 5; 6 залишалось одне яйце, то їх було: 61, або 121, або 181, або 241 і т. д. Так як їх було не більше 140, то цій умові задовольняють лише 2 числа 61 і 121. При розкладанні по 7 залишилось 2 яйця. Цій умові задовольняє число 121. Отже, яєць було 121.
1110. Нехай 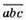 – дане число,
– дане число, 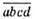 – число, одержане після дописування цифри d. Тоді
– число, одержане після дописування цифри d. Тоді
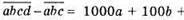
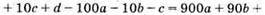
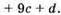
Так як різниця ділиться на 9, то d повинно ділитися на 9. Отже, d = 9.
Відповідь: дописали цифру 9.
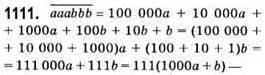
Ділиться на 37, бо 111 ділиться на 37. Тому 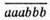 ділиться на 37.
ділиться на 37.
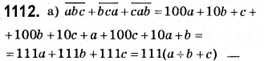
Ділиться на 111, отже, 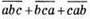 – ділиться на 111.
– ділиться на 111.
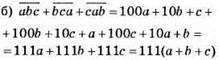 – це число може бути представлено у вигляді квадрату натурального числа лише за умови, що а + b + с = 111, але це неможливо, бо а, b, с – цифри (одноцифрові числа), тому сума їх не може дорівнювати 111. Отже, не існує такого числа
– це число може бути представлено у вигляді квадрату натурального числа лише за умови, що а + b + с = 111, але це неможливо, бо а, b, с – цифри (одноцифрові числа), тому сума їх не може дорівнювати 111. Отже, не існує такого числа 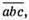 для якого дане число може бути представлене у вигляді квадрату натурального числа.
для якого дане число може бути представлене у вигляді квадрату натурального числа.
1113. а) n = 10. Якщо число складається з парної кількості цифр, то останню цифру записує другий учень і він завжди досягне своєї мети. Першу цифру пише перший учень, а другий учень пише цифру, яка в сумі з першою цифрою дає 9. У десятицифровому числі 5 пар цифр. В останній парі: якщо перший учень напише цифру 9, то другий може дописати теж цифру 9, тобто доповнити її до 18. Сума цифр в кожній парі ділиться на 9, тому і сума цифр всього числа ділиться на 9. Отже, одержане число ділиться на 9.
Б) n = 15. Якщо число містить непарну кількість цифри, то останню цифру пише перший учень і йому не складно порахувати суму цифр уже записаних і дописати таку цифру, щоб сума записаних цифр не ділилась на 9. Тому в цьому випадку другий учень не зможе досягти мети, якщо перший йому буде заважати.
До § 2. Одночлени
1114. а) 34n + 4 = (34)n + 4 = 81n + 4 ділиться на 5, бо число 81n закінчується на 1 при любому значенні n, тоді 81n + 4 закінчується цифрою 5 при любому n, а тому ділиться на 5.
Б) 92n – 1 = (92)n – 1 = 81n – 1 ділиться на 10, бо число 81n закінчується цифрою 1, тоді 81n – 1 закінчується цифрою 0, тому ділиться на 10.
1115. 42n + 4 = (42)n + 4 = 16n + 4 ділиться на 10, бо 16n закінчується цифрою 6, тоді 16n + 4 закінчується цифрою 0.
1116. 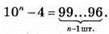
Це число записане цифрами 9, їх (n – 1) шт. і в найнижчому розряді цифра 6. Тому це число ділиться на 3 (і 9, і 6 діляться на 3), але не ділиться на 9, бо 6 не ділиться на 9.
1117. m(m + 1) = 3n + 2n. Якщо m – натуральне число, то m і m + 1 – два послідовних числа. Одне з них парне, друге – непарне, тоді m(m + 1) – парне число. Якщо n – натуральне, то 3n – непарне число, 2n – парне. Тоді 3n + 2n – число непарне.
Оскільки непарне і парне число не можуть бути рівними, то рівність m(m + 1) = 3n + 2n не може виконуватися при любих m і n.
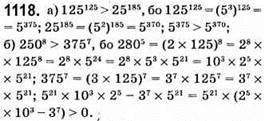
1119. Квадрат цілого числа може закінчуватися цифрами 0; 1; 4; 9; 6.
Четверта степінь цілого числа – це квадрат квадрату числа а4 = (а2)2 і може закінчуватися цифрами 0; 1; 6.
Восьма степінь цілого числа – це квадрат четвертої степені числа а8 = (а4)2 і може закінчуватися цифрами 0; 1; 6.
1120. а) Цілого числа а не існує, щоб квадрат цього числа дорівнював 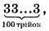 бо квадрат цілого числа не може закінчуватися цифрою 3.
бо квадрат цілого числа не може закінчуватися цифрою 3.
Б) Чисел m і n, для яких рівність m4 = 10n + 4 – правильна, не існує, бо m4 може закінчуватися цифрою 0; 1; 6, а 10n + 4 при любому n закінчується цифрою 4.
В) Чисел m і n, для яких рівність m8 = 10n + 2 – правильна, не існує, бо m8 може закінчуватися цифрою 0; 1; 6, а 10n + 2 закінчується цифрою 2.
1121. 2 • n = m2; 2 • n = (2 • 2) • (2 • 2) = 42, n = 8; 3 • n = а3; 3 • n = 3 • 1 • 1 • 1 • 3 • 13 = 33, n = 9. Щоб ці умови виконувалися одночасно, треба знайти НСК(8; 9) = 72.
2 • 72 144 = 122; 3 • 72 = 216 = 63. Отже, n = 72.
До § 3. Многочлени
1122. а) n = 6а + 3; m = 6b + 4; 3n = 18а + 9; 5m = 30b + 20;
3b + 5n = 18а + 30b + 29 = 6(3а + 5b + 4) + 5.
При діленні числа 3n + 5n на 6 остача 5.
M • n = 36qb + 42b + 18b + 12 = 6(6аb + 4а + 3b + 2).
При діленні числа mn на 6 остача 0.
Б) m = 5а + 2; n = 5b + 3; k = 5с + 4.
Nk – m(m – 1) = (5b + 3)(5с + 4) – (5а + 2)(5а + 1) = 25bс + 20b + 15с + 12 – 25а2 – 5а – 10а – 2 = 25bс + 20b + 15с + 10 – 25а2 – 15а = 5(5bс + 4b + 3с + 2 – 5а2 – 3а) ділиться на 5.
1123. Нехай число одиниць х, тоді десятків і тисяч а + 1, а сотень а + 2.
Тоді дане число 1000(х + 1)+ 100(х + 2) + 10(x + 1) + x = 1000х + 1000 + 100х + 200 + 10х + 10 + х = 111х + 1210 = 11 • (101х + 110) ділиться на 11.
1124. Нехай 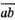 – дане число, тоді друге число –
– дане число, тоді друге число – 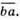 Тоді
Тоді
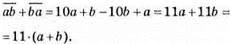
Число 11(а + b) можна подати у вигляді квадрату натурального числа, коли а + b = 11 (а > b). Тоді шукані двоцифрові числа: 65; 74; 83; 92.

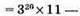 ділиться на 11.
ділиться на 11.
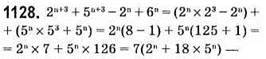
Ділиться на 7.
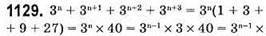
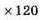 ділиться на 120.
ділиться на 120.
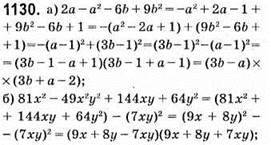
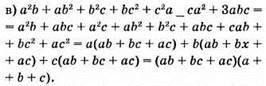
До § 4. Формули скороченого множення
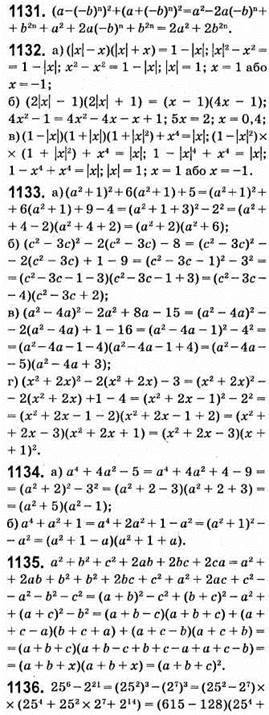
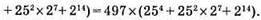
1137. Нехай а і b – цілі числа. Тоді a = 5n + 1; b = 5k + 2.
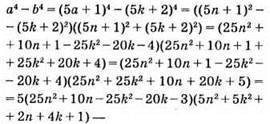
Кратно 5, т. к. множник 5 кратний 5.
1138. m2 – n2 = (m – n)(m + n) – це число може бути простим, коли один з множників дорівнюватиме 1. Так як m – n < m + n, то m – n = 1. Звідси m = n + 1.
1139. а) (m + n)2 – n2 =3; m2 + 2mn + n2 – n2 = 3; m2 + 2mn = 3; m(m + 2n) = 3;
M = 1, тоді m + 2n = 3; 2n = 2; n = 1;
M = 3, тоді m + 2n = 1; не має змісту.
Відповідь: m = 1; n = 1.
Б) m2 – (m – n)2 = 0; m2 – m2 + 2mn – m2 = 9; 2mn – n2 = 9; n(2m – n) = 0;
N = 1; 2m – n = 0; 2n = 10; n = 5;
N = 3; 2m – n = 3; 2m = 6; m = 3;
N = 9; 2m – n = 1; 2m = 10; m = 5.
Відповідь: n = 1, m = 5; n = 3, m = 3; n = 9, m = 5.
1140. (n + 2m)2 – (n + m)2 = 5; (n + 2m – n – m)(n + 2m + n + m) = 5; m(2n + 3m) = 5;
1) m = 1, тоді 2n + 3m = 5; 2n = 2; n = 1;
2) m = 5, тоді 2n + 3m = 1; 2n = -14; n = -7;
3) m = -1, тоді 2n + 3m = -5; 2n = -2; n = -1;
4) m = -5, тоді 2n + 3m = -1; 2n = 14; n = 7.
1141. а) m3 – (m – 2n)3= 99; (m – m + 2n) • (m2 + m(m – 2n) + (m + 2n)2) = 99;
2n(n2 + m(m – 2n) + m) – 2n)2) = 99.
В лівій частині рівності число парне, в правій – непарне. Тому ця рівність не може виконуватися при любих m і n.
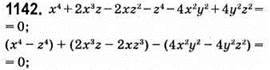
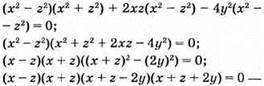
Рівність виконується, якщо у – середнє арифметичне чисел х і z, тобто 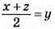 або х + z = 2у, тоді х + z – 2у = 2у – 2у = 0.
або х + z = 2у, тоді х + z – 2у = 2у – 2у = 0.
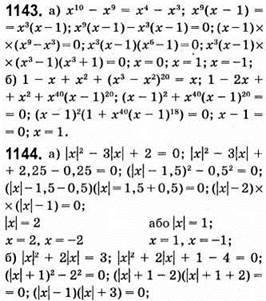

X = 1 або х = -1.
Або |x| + 3 = 0; немає розв’язків;
1145. х2 – 4х + |х| + 5 = 0; х2 – 4х + 4 + |х| + 1 = 0; (х – 2)2 + |х| + 1 = 0.
Рівняння не має коренів, бо (х – 2)2 + |х| ≠ -1 при любих значеннях х.
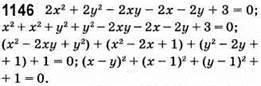
Рівність не може виконуватися, бо (х – y)2 + (х – 1)2 + (y – 1)2 ≠ -1.
1147. Ціле число може мати вигляд:
1) n = 3k; 2) n = 3k + 1; 3) n = 3k + 2.
1) (3k)2 = 9k2 – ділиться на 3;
2) (3k + 1)2 = 9k2 + 6k + 1 при діленні на 3 дає остачу 1;
3) (3k + 2)2 = 9k2 + 12k + 4 = 9k2 + 12k + 3 + 1 при діленні на 3 дає остачу 1.
До § 5. Функції
1150. І: 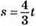 або
або 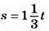
II: s = 1,5t
Переможцем є другий хлопець.
Через 45 с після старту І пройшов 60 м, a II – 67,5 м.
II хлопець на відстані 100 м буде через 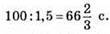
За цей час І хлопець пройде відстань 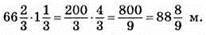
Між ними відстань буде 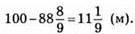
1151. y = kx + b.
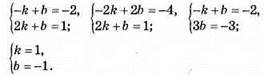
У = x – 1 – графік даної функції. (2а; 2 – а) належить графіку, тоді 2а – 1 = 2 – а; 3а = 3; а = 1.
До § 6. Лінійні рівняння з однією змінною
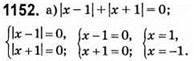
Відповідь: коренів немає.
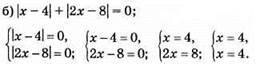
Відповідь: х = 4.
1153. а) |х – а| = 0; х = а = 0; х = а. Рівняння має 1 корінь.
Б) |х| = а. Якщо а < 0, то рівняння коренів не має.
Якщо а = 0, то рівняння має 1 корінь, х = 0.
Якщо а > 0, то рівняння має 2 кореня: x = а і х = – а.
Б) |х – а| + |х – 1| = 0. Рівняння має 1 корінь, х = 1 при а = 1.
Якщо а ≠ 1, то рівняння коренів не має.
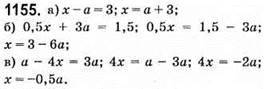
1156. а) ах = 5; х = 5/a.
Якщо а = 0, рівняння не має розв’язків.
Якщо а ≠ 0, рівняння має 1 корінь.
Б) ах = 0; х = 0/a.
Якщо а = 0, рівняння має безліч коренів.
Якщо а ≠ 0, рівняння має 1 корінь: х = 0.
В) аx = 10а.
Якщо а = 0, рівняння має безліч коренів.
Якщо а ≠ 0, то рівняння має 1 корінь: x = 10.
Г) (а + 2)x = 2; 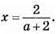 -.
-.
Якщо а = -2, то рівняння не має коренів.
Якщо а ≠ -2, то рівняння має 1 корінь.
Д) 4аx + 4а = 8а; 4а(x + 1) = 8а.
Якщо а = 0, то рівняння має безліч коренів.
Якщо а ≠ 0, то рівняння має 1 корінь: 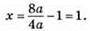
Е) а(1 – х) = 5а.
Якщо а = 0, то рівняння має безліч коренів.
Якщо а ≠ 0, то рівняння має 1 корінь: x = -4.
1157. а) (b – 2)х = b2 – 4; (b – 2)х = (b – 2) • (b + 2).
Якщо b = 2, то рівняння має безліч коренів.
Якщо b ≠ 2, то рівняння має 1 корінь: х = b + 2.
Б) bх – 2х = 2b – 4; x(b – 2) = 2(b – 2).
Якщо b = 2, то рівняння має безліч коренів.
Якщо b ≠ 2, то рівняння має 1 корінь: х = 2.
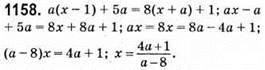
Якщо а = 8, рівняння не має коренів. При всіх інших значеннях а рівняння має 1 корінь.
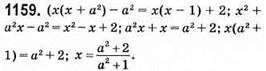
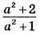 – додатне при будь-якому значенні а, бо а2 + 2 – додатне і а2 + 1 – додатне.
– додатне при будь-якому значенні а, бо а2 + 2 – додатне і а2 + 1 – додатне.
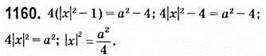
Якщо а = 0, рівняння має 1 корінь: х = 0.
Якщо а ≠ 0, рівняння має 2 кореня: х = ±a/2.
1161. х2 – 12х + 30 = а; (х2 – 12х + 36) – 6 = а; (х – 6)2 = а + 6.
Якщо а = -6, рівняння має 1 корінь: х = 6.
А = -6 – найменше значення, для якого рівняння має хоча б один корінь.
1162. Нехай з моменту першої зустрічі до другої зустрічі автобус їхав х годин і проїхав 60х км. За цей час автомобіль їхав 1/3 год до міста А, 40 хв = 2/3 год відпочивав, тому з п. А до моменту другої зустрічі був у дорозі 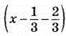 год і проїхав 90(х – 1) км. Відстань, яку проїхав автомобіль, на 30 км більша. Тому 90(х – 1) – 60х = 30; 90х – 60х = 120; 30x = 120; х = 4.
год і проїхав 90(х – 1) км. Відстань, яку проїхав автомобіль, на 30 км більша. Тому 90(х – 1) – 60х = 30; 90х – 60х = 120; 30x = 120; х = 4.
Відстань від А до моменту другої зустрічі 90 • (4 – 1) = 270 км. Тоді відстань від А до В дорівнює 270 + 20 = 290 км.
1163. Нехай міді було х г, тоді олова 1,2x г, а цинку 1,8x г. За умовою задачі х + 1,2x + 1,8x = 1000; 4х = 1000; х = 250 г міді було у сплаві.
1,2 • 250 = 300 голова у сплаві; 300 • 1,5 = 450 г цинку у сплаві.
Відповідь: 450 г.
1164. Нехай місткість чашки х мл. Після 1 доливання молока в чашці 4/5x кави + 1/5х молока. Після другого доливання 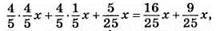 де 16/25х – кава; 9/25х – молокo. За умовою задачі
де 16/25х – кава; 9/25х – молокo. За умовою задачі 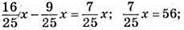
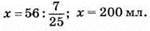
1165. Нехай велосипедист їхав зі швидкістю x км/год. Якби він збільшив швидкість на 2 км/год, то вона б становила (x + 2) км/год. Із збільшеною швидкістю велосипедист їхав би у год, з меншою 1,1 у год. Тоді x • 1,1у = (x + 2) • у; 1,1ху = xy + 2у; 1,1xy – ху – 2у = 0; 0,1xy – 2y = 0; 0,1y(x – 20) = 0; y = 0 – не має змісту або x – 20 = 0, x = 20.
Відповідь: 20 км/год.
До § 7. Системи лінійних рівнянь із двома змінними
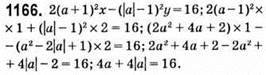
Якщо а > 0: 4а + 4а = 16; 8а = 16; а = 2, то розв’язком рівняння є пара чисел (1; 2).
Якщо а < 0, то рівняння розв’язків не має.
Відповідь: а = 2.
1167. а) 3n – 7m = 5; 3n = 5 + 7m; 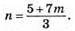
Якщо m = 1, то n = 4; m = 4, n = 11; m = 7, n = 18; …; m = 1 + 3а, n = 4 + 7а, де а – любе ціле число.
Б) n2 – m2 = 9; (n – m)(n + m) = 9;
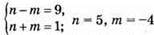 або
або
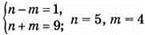 або
або
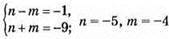 або
або
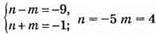 або
або
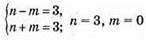 або
або
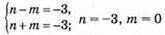
1168. |x| – |y| = 0.
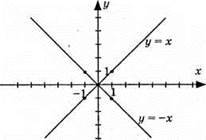
I коорд. кут: x > 0; y > 0; x – y = 0 або у = x.
II коорд. кут: x < 0; y > 0; – x – у = 0 або у = – х.
III коорд. кут: x < 0; у < 0; – x + y = 0 або y = x.
IV коорд. кут: x > 0; у < 0; x + у = 0 або y = – х.
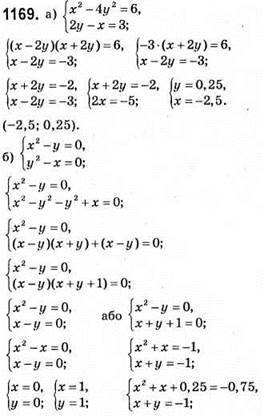
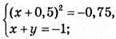
Система не має розв’язків.
Відповідь: (0; 0); (1; 1).
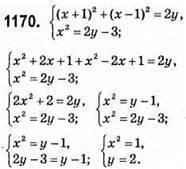
Звідси 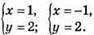
Відповідь: (1; 2); (-1; 2).
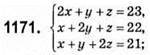
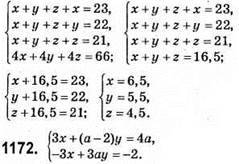
Якщо 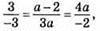 то система має безліч розв’язків.
то система має безліч розв’язків.
9а = -3а + 6; 12а = 6; а = 0,5.
Отже, якщо а = 0,5, то система має безліч розв’язків.
Якщо а ≠ 05, то система має 1 розв’язок.
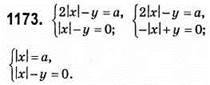
Система має два розв’язки, якщо а > 0.