Загальні відомості про рівняння
Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ
& 22. Загальні відомості про рівняння
Упродовж багатьох століть алгебра розвивалась як наука про рівняння.
Основні відомості про рівняння ви вже знаєте з попередніх класів. Нагадаємо, що вираз, записаний в рівнянні ліворуч від знака рівності, називають лівою частиною рівняння, а вираз, записаний праворуч, – правою частиною рівняння. Якщо в рівняння 4х – 6 = х замість змінної х підставити число 2, то одержимо правильну числову рівність 4 ∙ 2 – 6 – 2, оскільки числові значення обох частин
Рівняння можуть мати різну кількість коренів. Наприклад, рівняння 4х – 6 = х має лише один корінь число 2. Рівняння х(х – 6) = 0 має два корені числа 0 і 6. Будь-яке значення змінної х задовольнятиме рівняння х + 0,1 = 0,1 + х, тому будь-яке число є його розв’язком, отже, це рівняння має безліч коренів. Але не існує жодного значення змінної х, яке б перетворювало рівняння х + 1 = х у правильну числову рівність, оскільки при кожному значенні змінної х значення лівої частини рівняння буде на 1 перевищувати
Розглянемо рівняння х + 1 = 5 і 3х = 12. Кожне з них має єдиний корінь – число 4. Ці рівняння є рівносильними.
Приклад 1. З’ясувати, чи є рівносильними рівняння:
1) 18 – х = 11 і 21 : х = 3;
2) х + 3 = х і 2 – х = 5 – х;
3) х + 3 = 4 і 5х = 10?
Р о з в ‘ я з а н н я. 1) Коренем рівняння 18 – х = 11 є число 7. Коренем рівняння 21 : х = 3 також є число 7. Тому рівняння 18 – х = 11 і 21 : х = 3 – рівносильні.
2) Обидва рівняння x + 2- x і 2 – х = 5 – х не мають коренів, тому є рівносильними.
3) Коренем рівняння х + 3 = 4 є число 1, а коренем рівняння 5х = 10 – число 2. Тому рівняння х + 3 = 4 і 5х = 10 не є рівносильними.
Під час розв’язування рівнянь використовують властивості, які перетворюють рівняння на рівносильні їм рівняння:
Приклад 2. З’ясувати, чи є рівносильними рівняння:
1) 2(х – 1) = 5х і 2х – 2 = 5х;
2) 3а + 2 = 5а – а – 7 і 3а + 2 = 4а – 7;
3) 5х = 2х + 9 і bх – 2х = 9;
4) 0,5b = 1,5b – 3,5 і b = 3b – 7.
Р о з в ‘ я з а н н я. 1) Рівняння 2(х – 1) = 5х і 2х 2 = 5х є рівносильними, оскільки друге рівняння одержуємо з першого розкриттям дужок у його лівій частині.
2) Рівняння 3а + 2 = 5а – а – 7 і 3а + 2 = 4а – 7 – рівносильні, оскільки друге рівняння одержуємо з першого зведенням подібних доданків у його правій частині.
3) Рівняння 5х = 2х – 9 і 5х – 2х = 9 – рівносильні, оскільки друге рівняння одержуємо з першого перенесенням доданка з правої частини рівняння в ліву із зміною знака цього доданка на протилежний.
4) Рівняння 0,5b = 1,5b – 3,5 і b = 3b – 7 – рівносильні, оскільки друге рівняння одержуємо шляхом множення на 2 обох частин першого рівняння.
У IX ст. видатний арабський математик
А ще раніше…
Мухаммед бен Муса аль-Хорезмі у своєму трактаті “Кітаб аль-джебр аль-мукабала” зібрав і систематизував існуючі на той час методи розв’язування рівнянь. Узятий з назви цієї книжки термін “аль-джебр” (у перекладі з арабської означає “відновлення”) надалі почав уживатися як “алгебра” і дав назву цілій науці.
У ті часи, коли аль-Хорезмі писав свій трактат, від’ємні числа вважалися хибними, несправжніми. Тому коли від’ємне число переносили з однієї частини рівняння в іншу, змінюючи його знак, вважали, що воно “відновлюється” (стає додатним), тобто з несправжнього перетворюється на справжнє. Саме таке перетворення рівнянь аль-Хорезмі і назвав “відновленням”.
Властивість взаємного знищення однакових доданків рівняння, що містилися в обох його частинах, аль-Хорезмі назвав “протиставленням” (арабською мовою – “аль-мукабал”).
Аль-Хорезмі був перший учений, хто відокремив алгебру від арифметики і розглянув її як окрему математичну науку. Алгебру аль-Хорезмі в латинському перекладі вивчали європейці протягом XII-XVI ст. Подальший розвиток алгебри пов’язаний саме з європейськими вченими, зокрема з італійськими математиками епохи Відродження.
До XIX ст. алгебра розвивалася як наука, що вивчає методи розв’язування рівнянь. Згодом вона значно збагатилася новими змістовими лініями: спрощення виразів, функції, розв’язування нерівностей тощо, і тепер рівняння – це лише одна зі складових частин алгебри.
Мухаммед бен Муса аль-Хорезмі (783 – бл. 850)
Що називають рівнянням? Що називають коренем (або розв’язком) рівняння? Що означає розв’язати рівняння? Які рівняння називають рівносильними? Які властивості використовують під час розв’язування рівнянь?
831. (Усно) Який із записів є рівнянням (відповідь обгрунтуйте):
1) 7х – 21 > 0;
2) 4х + 5;
3) 7х – 2 = 10;
4) (12 – 10) ∙ 3 = 6?
832. (Усно) Чи є число 3 коренем рівняння:
1) 2х = 6;
2) х – 7 = 4;
3) 2х + 3 = 8;
4) 27 : х = 9?
833. Чи є число 2 розв’язком рівняння:
1) х + 7 = 9;
2) 5х = 12;
3) х – 8 = -6;
4) х : 4 = 2?
834. Яке із чисел є коренем рівняння х2 – 2х + 3:
1) 0; 2) -1; 3) 1; 4) 3?
835. Чи є коренем рівняння х2 = 4 – 3х число:
1) 0; 2) 1; 3) -2; 4) -4?
836. Доведіть, що кожне із чисел 1,3 та -1,3 є коренем рівняння х2 = 1,69.
837. Чи є рівносильними рівняння:
1)х + 2 = 5 і х : 3 = 1;
2)х – 3 = 7 і 2х = 18?
838. Чи є рівносильними рівняння:
1) х – 2 = 3 і 2х= 10;
2) х + 3 = 7 і х : 2 = 3?
839. Доведіть, що:
1) коренем рівняння 2(х – 3) = 2х – 6 є будь-яке число;
2) рівняння у – 7 = у не має коренів.
840. Доведіть, що:
1) коренем рівняння 3(2 – с) = 6 – 3с є будь-яке число;
2) рівняння х = х + 8 не має коренів.
841. Складіть рівняння, що має:
1) єдиний корінь число -2;
2) два корені – числа 5 і -5.
842. З’ясуйте, не розв’язуючи рівнянь, чи є вони рівносильними:
1) 4(х – 2) = 19 і 4х – 8 = 19;
2) 2х – 3 = 3х + 5 і 2х – 3х = 5 + 3;
3) 8(х – 3) = 40 і х – 3 = 5;
4) 
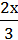= 11 і 2х = 33.
843. Установіть, не розв’язуючи, чи є рівняння рівносильними:
1) 8(х – 1) = 5 і 8х – 8 = 5;
2) 3х + 7 = 4х – 8 і 3х – 4х = -8 – 7;
3) 9(х + 2) = 18 і х + 2 = 2;
4) – 
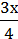= 7 і -3х = 28.
844. Чи має розв’язки рівняння:
1) х + 2 = 2 – х;
2) х + 3 = 3 + х;
3) х + 1 = -1 + х;
4) 0 – х = 0;
5) 0 ∙ (х – 1) = 3;
6) 5(х – 1) = 5х – 5;
7) 0 : х = 0;
8) 2(х – 3) = 2х – 7?
Вправи для повторення
845. Знайдіть значення виразу:
1) 4а – 12b + 8а, якщо а = -13; b = 13;
2) (3х – 2х)(5m + 4m), якщо х = 1 
; m = -1 
.
846. Спростіть вираз:
1) 64 – (8 – 3m)2;
2) a2b2 – (ab + 7)2;
3) t2 + 25 – (t – 5)2;
4) р4 – 16 – (p2 + 4)2.
Цікаві задачі для учнів неледачих
847. Яку остачу при діленні па 1001 дає число
1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 ∙ 7 ∙ 8 ∙ 9 ∙ 10 ∙ 11 ∙ 12 ∙ 13 + 2000?
(1 votes, average: 5.00 out of 5)
Loading...