Завдання для перевірки знань до §§ 19-21
1. 1) у = х2 + х; 3) 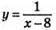 – функції.
– функції.
2. 1) у = 3х – 7; 3) у = 4 – лінійні функції.
3. 1) у = -2х + 6; k = -2; l = 6;
2) у = 7,4x; k = 7,4; l = 0.
4. у = -2х + 7;
1) х = 5; y = -2 • 5 + 7 = -10 + 7 = -3.
Відповідь: х = 5, у = -3.
2) у = 3; 3 = -2х + 7; 2х = 7 – 3; 2х = 4; х = 2.
Відповідь: х = 2, у = 3.
5. у = 2х – 5;
X | 0 | 1 |
У | -5 | -3 |
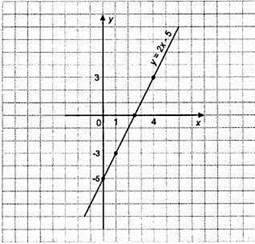
1) Якщо х = 4, то у = 3.
2) Якщо у = -3, то х = 1.
6. у = 0,8х – 7,2.
1) Нулі функції: 0,8х – 7,2 = 0; 0,8х = 7,2; х = 7,2 : 0,8; х = 9.
2) А(10; 1). у = 0,8 • 10 – 7,2 = 8 – 7,2 = 0,8. Графік не проходить через точку А(10; 1).
7. 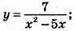 х2 – 5х ≠ 0; х(х – 5) ≠ 0; х ≠ 0, х ≠ 5.
х2 – 5х ≠ 0; х(х – 5) ≠ 0; х ≠ 0, х ≠ 5.
Відповідь: область визначення функції – усі числа, крім 0 і 5.
8. Побудуємо в одній системі координат графіки функцій у = -2,5х і у = -5 та знайдемо координати точок їх перетину.
Y = -2,5х | У = -5 | |||||
X | 0 | 2 | X | 0 | 2 | 4 |
Y | 0 | -5 | У | -5 | -5 | -5 |
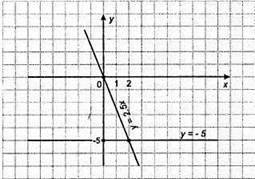
Графіки перетинаються
9. у = х2 – 6х + 11. Найменше значення функції: y = 2.
У = (х2 – 6x + 9) – 9 + 11;
У = (х – 3)2 + 2.
10. у = 3х – 7; -2 ≤ х ≤ 5.
X | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
Y | -13 | -10 | -7 | -4 | -1 | 2 | 5 | 8 |
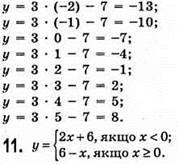
Y = 2х + 6 | Y = 6 – x | |||||
X | -1 | -2 | X | 0 | 2 | 6 |
У | 4 | 2 | Y | 6 | 4 | 0 |
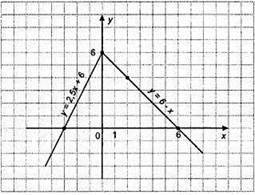
1) Нулі функції: х = -3, у = 6.
2) Функція набуває додатніх значень при -3 < x < 6.
3) Функція набуває від’ємних значень: х є (-∞; -3) ∪ (6; +∞); х < -3 та х > 6.
Related posts:
- Завдання для перевірки знань за курс алгебри 7 класу 1. 1) х – 2 = 5; 7 – 2 = 5; 5 = 5; 7 – корінь рівняння; 2) 56 : х = 6; 56 : 7 = 8; 8 ≠ 6; 7 – не є корінь рівняння. 2. 1) p4 • p3 = р7; 2) t9 : t5 = t4. 3. 1) х […]...
- Завдання для перевірки знань до §§ 25-30 1. 1) 2х + 3у = 9. 2. Розв’язком рівняння 2х + у = 7 є пара чисел (4; -1). 3. Розв’язком системи рівнянь є пара чисел (7; 4). 4. Y = 3х У = -2х – 5 X 0 1 X 0 -1 У 0 3 Y -5 -3 Відповідь: (-1; -3). Відповідь: (2; […]...
- Завдання для перевірки знань до §§ 22-24 1. 1) Ні; 2) 3х = 12; х = 12 : 3; x = 4 – корінь. 2. 1) 5х = -2; 4) 0 • х = 0. 3. 1) -3х = 5; х = -5/3; 1 корінь; 2) 0 • х = 7; немає коренів. 4. 1) -4х = 12; х = -3; 2) […]...
- Завдання для перевірки знань за курс алгебри 7 класу Завдання для перевірки знань за курс алгебри 7 класу 1. Перевірте, чи є число 7 коренем рівняння: 1) х – 2 = 5; 2) 56 : х = 6. 2. Виконайте дії: 1) р4р3; 2) t9 : t5. 3. Чи проходить графік рівняння х – у = 5 через точку: 1) M(6; 2); 2) N(4; […]...
- Повторення та систематизація знань та вмінь учнів з теми “Функції і графіки” Урок № 85 Тема. Повторення та систематизація знань та вмінь учнів з теми “Функції і графіки” Мета: повторити та систематизувати набуті учнями знання про зміст основних понять теми та види задач; повторити та систематизувати основні способи дій, що були опановані учнями під час вивчення теми; провести підготовку до підсумкового тематичного оцінювання. Тип уроку: повторення та […]...
- ДЕСЯТЬ ЗАВДАНЬ ДЛЯ ПЕРЕВІРКИ ЗНАНЬ СВІТ МУЗИЧНИХ ТВОРІВ ДЕСЯТЬ ЗАВДАНЬ ДЛЯ ПЕРЕВІРКИ ЗНАНЬ 1. Що таке музика? Що допомагає музиці “спілкуватися” зі слухачем? Обери правильну відповідь: 2. Хто створює музику? Назви кількох композиторів. Яка музика не має конкретного автора? 3. Хто виконує музику? Обери відповіді та поясни їх: Композитор, піаніст, баяніст, співак, поет, диригент. 4. Як назвати виконавця, який співає […]...
- Функції та їхні властивості. Квадратична функція УРОК № 62 Тема. Функції та їхні властивості. Квадратична функція Тестові завдання 1. Знайдіть область визначення функції . А) х 5; Б) х -5; В) х -5, х 0; Г) х 3, х -5, х 0. 2. Знайдіть нулі функції . А) 0; 2; б) 2; в) 0; -2; г) нулів немає. 3. Яка з […]...
- 5 вправа 648-769 648. х – довжина сторони квадрата; S – площа квадрата; Х – незалежна змінна; у – залежна змінна. S = х2. 649. у = 5х; х – аргумент; у – функція. А) Якщо х = 2, то y = 5 • 2 = 10; якщо х = -1, то у = 5 • (-1) = […]...
- Вправи для повторення розділу 2 До § 19. 819. Площа квадрата залежить від довжини його сторони. Площа квадрата є функцією від довжини сторони квадрата: S = х2. Якщо сторона квадрата а, то площа S = а2. 820. X -4 -2 0 2 4 Y 2/7 0 -2/3 -4 6 G 8/5 -6/5 -4/5 -2/5 0 821. у = 48 – […]...
- Обернені функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Обернені функції Дві функції називаються оберненими, якщо вони виражають ту саму залежність між змінними величинами, але в одній з них за аргумент прийнято х, а за функцію – у, в іншій – навпаки, тобто за аргумент прийнято у, а за функцію – х. Функції у = f(x) […]...
- Схема дослідження – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Функцією (або функціональною залежністю) називається закон, за яким кожному значенню незалежної змінної х з деякої множини чисел, що називається областю визначення функції, ставиться у відповідність тільки одне певне значення величини у. Графіком функції називається множина всіх точок координатної площини з координатами (х, у), такими, при яких абсциса […]...
- Зростаючі й спадні функції Математика – Алгебра Числові функції Зростаючі й спадні функції Функція називається Зростаючою на деякому інтервалі, якщо для будь-яких двох значень аргументу з цього інтервалу більшому значенню аргументу відповідає більше значення функції. Функція називається Спадною На деякому інтервалі, якщо для будь-яких значень аргументу з цього інтервалу більшому значенню аргументу відповідає менше значення функції. Приклади 1) y […]...
- Вправи на закріплення знань про правила перевірки ненаголошених е, и в корені слова. Складання усної розповіді на тему “Зустріч птахів” Урок 90 Тема. Вправи на закріплення знань про правила перевірки ненаголошених е, и в корені слова. Складання усної розповіді на тему “Зустріч птахів” Мета: продовжувати формувати вміння перевіряти ненаголошені е, и в корені; розширювати лексичний запас учнів; формувати навичку роботи з орфографічним словником; виховувати повагу до старших, до народних традицій, любов до природи і праці. […]...
- Поняття про обернену функцію УРОК 17 Тема. Поняття про обернену функцію Мета уроку: формування понять: оборотна функція, обернена функція. Вивчення алгоритму знаходження формули функції, оберненої до даної, властивості графіків взаємно-обернених функцій. І. Аналіз контрольної роботи II. Сприймання і усвідомлення нового матеріалу На уроках математики ви неодноразово розв’язували задачу: обчислити значення функції у = f(x) при заданому значенні х0 аргументу. […]...
- Степеневі функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Степеневі функції Графіки функції є параболами степеня n Графіки функції є гіперболами Функція y = ах, де а > 0, а ≠ 1, називається показниковою функцією з основою а. Приклад 0 < а < 1 Y = (1/2)x А > 1 Y = 2х Область визначення Х […]...
- Показникова функція, її графік і властивості УРОК 43 Тема. Показникова функція, її графік і властивості Мета уроку. Засвоєння учнями поняття показникової функції, її властивостей і графіка. Обладнання. Таблиця “Показникова функція”. І. Аналіз контрольної роботи II. Повідомлення теми уроку III. Сприймання і усвідомлення нового матеріалу Функція виду у = ах, де а > 0, а? 1, називається показниковою (з основою а). Усне […]...
- Огляд властивостей основних функцій УРОК 2 Тема. Огляд властивостей основних функцій Мета уроку: Повторення і узагальнення властивостей елементарних функцій: у = kx + b, у = , у = х2, у= х3, у = , у = , у = ?х2 + bx + с. І. Перевірка домашнього завдання 1. Один учень пояснює розв’язання вправи № 1 (5), другий […]...
- Графік функції. Графічний спосіб задання функції Розділ 2. ФУНКЦІЇ & 20. Графік функції. Графічний спосіб задання функції У 6 класі ми вже розглядали графік залежності між двома величинами. Розглянемо поняття графіка функції. Приклад 1. Нехай дано функцію у = + 3, де -2 ≤ х ≤ 3. Знайдемо значення цієї функції для цілих значень аргументу і занесемо результати в таблицю: Х […]...
- Числові функції Математика – Алгебра Числові функції Залежність змінної y від змінної x називається Функцією, якщо кожному значенню x відповідає єдине значення y. x називається Аргументом, або Незалежною змінною, y – Залежною змінною, або Функцією від x. Позначення: , і т. д. Множина значень, яких набуває незалежна змінна x, називається областю визначення функції. Позначення: , і т. […]...
- Обернені тригонометричні функції: у = arcsin х, у = arccos х УРОК 18 Тема. Обернені тригонометричні функції: у = arcsin х, у = arccos х Мета уроку: вивчення властивостей обернених тригонометричних функцій: у = arcsin х, у = arccos х. І. Перевірка домашнього завдання Математичний диктант. Закінчіть математичні твердження: 1. Функція, яка набуває кожного свого значення в єдиній точці області визначення називається… 2. Оберненою до функцій […]...
- Лінійна функція, її графік і властивості 849. Лінійною функцією є: 850. Прямою пропорційністю є функції: 851. y = 6x – 5 X -3 -2 -1 0 1 2 3 У -23 -17 -11 -5 1 7 13 852. 1) y = -2x + 5 Якщо x = -4, то у = -2 • (-4) + 5 = 13. Якщо x = […]...
- Дослідження властивостей функції і побудова її графіка Математика – Алгебра Похідна Дослідження властивостей функції і побудова її графіка Для того щоб дослідити функцію , треба: 1) знайти область визначення ; 2) знайти область значень ; 3) дізнатися про парність чи непарність функції ; 4) з’ясувати, чи є функція періодичною; 5) знайти нулі функції; точки перетину графіка з осями координат; 6) визначити проміжки, […]...
- Практичні завдання для самоконтролю знань – ВПРАВИ ДЛЯ САМОКОНТРОЛЮ ЗНАНЬ ЕКОНОМІЧНИЙ АНАЛІЗ ЧАСТИНА III. ФІНАНСОВИЙ АНАЛІЗ 7. АНАЛІЗ ФІНАНСОВОГО СТАНУ ПІДПРИЄМСТВА ВПРАВИ ДЛЯ САМОКОНТРОЛЮ ЗНАНЬ Практичні завдання для самоконтролю знань Завдання 1. На підставі даних звіту (додатки А, Б) визначте склад і структуру реальних активів. Порівняйте темпи зростання реальних активів з темпами зростання майна підприємства. Зробіть висновки за результатами аналізу. Завдання 2. На підставі даних […]...
- Властивості тригонометричних функцій – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Властивості тригонометричних функцій Функції У = sin x У = cos x Y = tg x 1. Область визначення Х (-∞;+∞) Х (-∞;+∞) X ≠ π/2 + πn, n Z 2. Множина значень Y Y Y (-∞;+∞) 3. Періодичність Усі тригонометричні функції – періодичні з найменшим додатним періодом Т […]...
- Функції та графіки Математика – Алгебра Функції та графіки Функція може задаватися описом, таблицею, графіком, формулою тощо. Область визначення функції зручно записувати за допомогою числових проміжків. Приклади 1) ; ; 2) ; ; 3) ; ; 4) ; . Пояснимо, як ми знайшли область визначення в останньому прикладі. Функція визначена для тих і тільки тих значень x, які […]...
- Розв’язування ірраціональних нерівностей УРОК 39 Тема. Розв’язування ірраціональних нерівностей Мета уроку. Познайомити учнів з узагальненим методом інтервалів. Формування умінь розв’язувати ірраціональні нерівності. І. Перевірка домашнього завдання 1. Перевірити розв’язування вправ № 71 (3), 67 (1), 79 (1) за розв’язаннями на дошці, заготовленими до уроку. 2. Самостійна робота Розв’яжіть рівняння: А) = . (4 бали) Б) – = 2. […]...
- Поняття про обернену функцію Математика – Алгебра Тригонометричні функції Поняття про обернену функцію Функція, яка приймає кожне своє значення в єдиній точці області визначення, є Оборотною. У такої функції за значенням залежної змінної можна однозначно визначити, якому значенню аргументу воно відповідає. Інакше кажучи, якщо функція є оборотною й число а належить до її області значень , то рівняння має […]...
- Функції та графіки. Лінійна функція Урок № 67 Тема. Функції та графіки. Лінійна функція Мета: повторити та узагальнити відомості щодо змісту основних понять теми; повторити, систематизувати набуті практичні вміння; провести підготовку до тематичної контрольної роботи. Тип уроку: узагальнення та систематизація знань, умінь, навичок. Хід уроку I. Організаційний момент 1. Готовність до уроку. 2. План роботи на уроці. II. Перевірка домашнього […]...
- Арифметичні операції над диференційовними функціями Математика – Алгебра Похідна Арифметичні операції над диференційовними функціями Теорема 1. Якщо функції і в точці мають похідні, то функція в цій точці також має похідну, яка дорівнює . Теорема 2. Якщо функції і в точці мають похідні, то в цій точці функція також має похідну, яка дорівнює . Наслідок. Якщо функція має похідну в […]...
- Розділ 4. Функції Або немає розв’язку. 6. 1) Так; 2) ні; 3) ні; 4) так. 7. 1) -4 = -2 • (-1)2 – 3 + 1; -4 = -2 – 3 + 1; -4 = -4; А належить графіку функції; 2) 0 ≠ -2 • 12 + 3 + 1; 0 ≠ -2 + 4; 0 ≠ 2; […]...