Знаходження площі трикутника за двома сторонами і кутом між ними
УРОК № 12
Тема. Знаходження площі трикутника за двома сторонами і кутом між ними
Мета уроку: виведення формули для знаходження площі трикутника за двома сторонами і кутом між ними. Формування вмінь застосовувати виведену формулу до розв’язування задач.
Тип уроку: комбінований.
Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника”[13].
Вимоги до рівня підготовки учнів: використовують формулу для знаходження площі трикутника за двома сторонами і кутом між ними під час розв’язування
Хід уроку
І. Перевірка домашнього завдання
Перевірити наявність виконаних домашніх завдань та відповісти на запитання, які виникли в учнів при виконанні домашнього завдання.
Задача 1. Розв’язання
Із трикутника ABC маємо: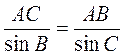 
, 
.
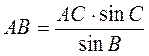Ураховуючи, що 
B = 180° – A – C = 180° – (? + ?), sinВ = sin(180° – (? + ?)) = sin(? + ?), а також, що sinC = sin?,
Маємо: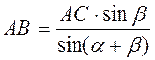 
.
Відповідь. .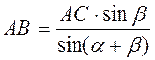
Задача 2. Розв’язання
; 
;
; 
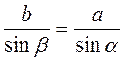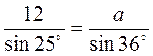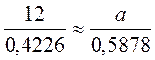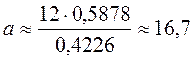.? = 180° – ? – ? 
180° – 36° – 25° = 119°.
; 
; 
; 
.
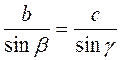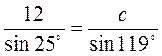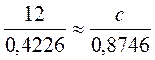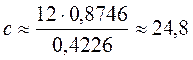Відповідь, а 16,7, с 24,8, ? 119°.
Самостійна робота (6 балів за кожне завдання).
Варіант 1
1. У трикутнику а = 37, ? = 70°, ? = 51°. Знайдіть b, с, ?. 2. У трикутнику a = 48, b = 35, ? = 65°. Знайдіть?, ?, с.
Варіант 2
1. У трикутнику а = 24, b = 13, с = 15. Знайдіть?, ?, ?. 2. У трикутнику а = 12, b = 10, ? = 40°. Знайдіть?, ?, с.
Відповіді до самостійної роботи
Варіант 1. 1. b 41, с 34, ? 59°.
2. с 47, ? 68°, ? 47°.
Варіант 2. 1. ? 118°, ? 28°, ? 34°.
2. ? 32°, ? 108°, с 17,8.
II. Повторення й систематизація знань учнів
Запитання до класу
1. Що таке площа? Сформулюйте властивості площі. 2. Чому дорівнює площа прямокутника? 3. Чому дорівнює площа квадрата зі стороною а? 4. Як зміниться площа прямокутника, якщо:
А) зменшити одну сторону вдвічі, а другу сторону залишити без змін;
Б) кожну сторону збільшити вдвічі?
5. Заповніть пропуски: 1км2 = … м2; 1 м2 = … см2; 1см2 = … мм2; 1 га = … м2; 1 а = … м2. 6. Чому дорівнює площа паралелограма? 7. Чому дорівнює площа трикутника, якщо відома його сторона а та висота па, проведена до неї?
III. Сприйняття й усвідомлення нового матеріалу
Вивчення теореми
Теорема. Площа трикутника дорівнює половині добутку двох будь-яких сторін на синус кута між ними.
Доведення
Нехай трикутник ABC – даний (рис. 40).
Доведемо, що S? ABC = 
AB • AC • sinA.
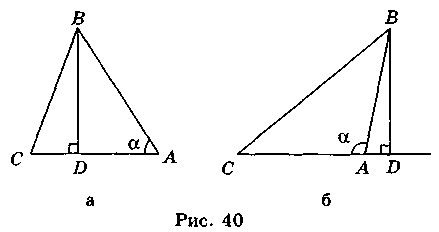
Проведемо у трикутнику ABC висоту BD. Маємо: S? АВС = AC • BD.
Якщо кут А гострий, то із трикутника ABD маємо: BD = AB • sin? (рис.40,а).
Якщо кут А прямий, то із трикутника DAB маємо: BD = AB • sin90° = АВ.
Якщо кут А тупий (рис. 40, б), то BD = AB • sin(180° – ?) = AB sin?.
Отже, S? ABC = AB • AC • sinA, що і треба було довести.
Розв’язування вправ
1) Знайдіть площу трикутника, дві сторони якого дорівнюють 6 см і 5 см, а кут між ними 30°. 2) Знайдіть площу правильного трикутника зі стороною а.
Розв’язання
Оскільки трикутник ABC рівносторонній (рис. 41), то АВ = АС = ВС = а, A = B = C = 60°.
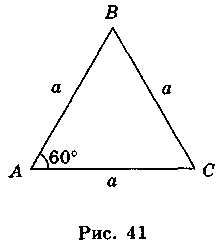
Тоді S = AB • AC • sinA = A • a • sin60° =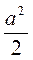 
• 
= 
.
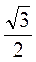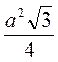Відповідь. .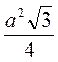
Учням слід порекомендувати запам’ятати цю формулу.
IV. Закріплення й осмислення нового матеріалу
Розв’язування задач
1. У трикутнику ABC АС = а, ВС = b. При якому куті С площа трикутника буде найбільшою?
Розв’язання
Оскільки S = AC • BC • sinC = Ab sinC, то значення S буде найбільшим, якщо sinC = 1, тобто C = 90°, тоді S = Ab.
Відповідь. 90°.
2. Доведіть, що площа паралелограма дорівнює добутку його сусідніх сторін на синус кута між ними: S = ab sin?, де а і b – сторони паралелограма, а? – кут між ними. 3. Суміжні сторони паралелограма дорівнюють 8 см і 6 см, а його гострий кут становить 30°. Знайдіть площу паралелограма. (Відповідь. 24см2) 4. Сторона ромба дорівнює 6 см, а один із кутів становить 150°. Знайдіть Площу ромба. (Відповідь. 18 см2) 5. Сторони паралелограма дорівнюють 9 см і 10 см, а площа становить 45 см2. Знайдіть кути паралелограма. (Відповідь. 30° і 150°) 6. Паралелограм і прямокутник мають однакові сторони. Знайдіть гострий кут паралелограма, якщо площа його дорівнює половині площі прямокутника.
Розв’язання
Нехай сторони паралелограма і прямокутника дорівнюють а і b (рис. 42).
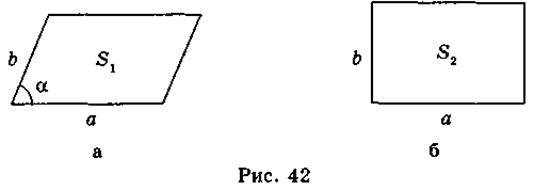
S1 = ab sin?, S2 = ab, де S1 – площа паралелограма, S2 – площа прямокутника, ? – гострий кут паралелограма. Ураховуючи, що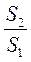 
= 2, маємо 
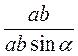= 2, звідси sin? = . Отже, ? = 30°.
Відповідь. 30°.
7. Знайдіть площу ромба, якщо його висота дорівнює 10 см, а гострий кут становить 30°.
Розв’язання
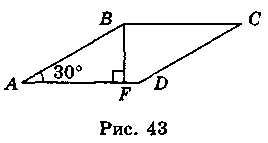
Нехай у ромбі ABCD (рис. 43) BF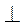
AD, BF = 10 см, BAD = 30°. Із прямокутного трикутника ABF маємо: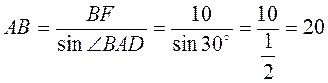 
(см). Отже, площа ромба: S = AD • BF = 20 • 10 = 200 (см2).
Відповідь. 200 см2.
8. Доведіть, що коли діагоналі чотирикутника перетинаються, то площа чотирикутника дорівнює половині добутку його діагоналей на синус кута між ними.
Розв’язання
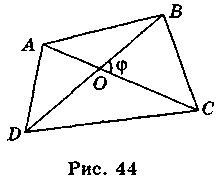
Нехай ABCD – довільний опуклий чотирикутник (рис. 44).
Доведемо, що SABCD = AC• BD • sin?, де? = BOC.
SABCD = S? BOC + S? AOB + S? AOD + S? DOC = BO • OC • sin? + АО • BO • sin(180° – ?) + АО • DO • sin? + DO • ОС • sin(180° – ?) =
= BO • OC sin? + АО • ВО • sin? + АО • DO • sin? + DO • OC sin? = (BO • OC + AO • BO + AO • DO + DO • OC) sin? =
= (BO • (AO + OC) + DO • (AO + OC)) sin? = (BO • АС + DО • АС) sin? = AC • (BO + DO) sin? = AC • BD sin?.
V. Домашнє завдання
1. Вивчити формулу для знаходження площі трикутника за двома сторонами і кутом між ними. 2. Розв’язати задачі. 1) Квадрат і ромб мають однакові периметри. Яка з фігур має більшу площу? Поясніть відповідь. 2) Знайдіть площу рівнобедреного прямокутного трикутника з гіпотенузою а. 3) Знайдіть площу рівнобедреного трикутника, у якого бічні сторони дорівнюють по 1 м, а кут між ними становить 70°.
VI. Підбиття підсумків уроку
Запитання до класу
1. Чому дорівнює площа трикутника, якщо відома його сторона і висота, проведена до цієї сторони? 2. Чому дорівнює площа трикутника, якщо відомі дві сторони і кут між ними? 3. Як знайти площу прямокутного трикутника, якщо відомі його катети?
(1 votes, average: 5.00 out of 5)
Loading...