Головна ⇒ 📌ГДЗ з математики ⇒ Зовнішній кут трикутника та його властивості

Зовнішній кут трикутника та його властивості

Розділ 3. Трикутники. Ознаки рівності трикутників

§ 18. Зовнішній кут трикутника та його властивості

438.

Зовнішній кут трикутника та його властивості

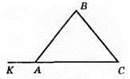
∠BAK – зовнішній кут при вершині А.

439.

Зовнішній кут трикутника та його властивості

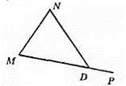
∠LDP – зовнішній кут при вершині D.

441. ∠A + ∠B = 70° – за властивістю зовнішнього кута трикутника.

442. Зовнішній кут трикутника при вершині С дорівнює 74° згідно з властивістю зовнішнього кута трикутника.

444. РК > PL, оскільки проти більшого кута трикутника лежить більша сторона (за умовою ∠L > ∠K).

445.

src="/images/image301_13.jpg" class=""/>

Згідно з теоремою 1 ∠KCA = ∠A + ∠B = 38° + 61° = 99°.

Відповідь: 99°.

446.

Зовнішній кут трикутника та його властивості

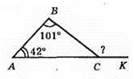
Згідно з теоремою 1 ∠BCK = ∠A + ∠B = 42° + 101° = 143°.

Відповідь: 143°.

448. Нехай? ABC – рівнобедрений. ∠KBC – зовнішній кут при вершині В. ∠KBC = ∠BAC + ∠BCA (згідно з теоремою 1). Отже, ∠BAC + ∠BCA = 110°, ∠BAC = ∠BCA = 50° (оскільки кути при основі рівнобедреного трикутника рівні).

Відповідь: 50°.

Зовнішній кут трикутника та його властивості

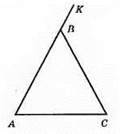
449.

Зовнішній кут трикутника та його властивості

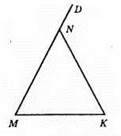
Нехай? DNK – рівнобедрений. ∠M = ∠K = 55°. ∠MNK – зовнішній кут при вершині N. За властивістю зовнішнього кута

маємо: ∠DNK = ∠M + ∠K = 55° + 55° = 110°.

Відповідь: 110°.

450.

Зовнішній кут трикутника та його властивості

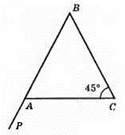
Нехай ∠CAP = 105° (зовнішній кут при вершині А), ∠C = 45°. ∠CAP = ∠B + ∠C – за властивістю зовнішнього кута трикутника. Звідси ∠В = ∠CAP – ∠C = 105° – 45° = 60°.

Відповідь: 60°.

451.

Зовнішній кут трикутника та його властивості

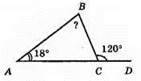
Нехай? BCD – зовнішній кут при вершині С, ∠A = 18°, ∠BCD = 120°. ∠BCD = ∠A + ∠B (за властивістю зовнішнього кута трикутника). Звідси ∠B = ∠BCD – ∠A = 120° – 18° = 102°.

Відповідь: 102°.

452.

Зовнішній кут трикутника та його властивості

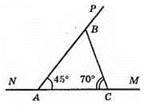
Нехай? ABC – даний трикутник, ∠A = 45°, ∠C = 70°.

∠PBC = ∠A + ∠C = 45° + 70° = 115° (за властивістю зовнішнього кута трикутника).

∠BCM = 180° – ∠C = 180° – 70° = 110° (як кут суміжний з кутом С).

∠NAP = 180° – ∠A = 180° – 45° = 135° (як кут суміжний з кутом А).

Відповідь: 115°, 110°, 135°.

453.

Зовнішній кут трикутника та його властивості

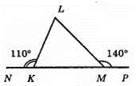
Нехай? KLM – даний трикутник, ∠NKL = 110°, ∠LMP =140°.

∠NKL + ∠LKM = 180°(як суміжні кути). Звідси ∠LKM = 180° – 110° = 70°.

∠LMР + ∠LKM = 180° (як суміжні кути). Звідси ∠LMK = 180° – 140° = 40°.

∠L + ∠LKM + ∠LMK = 180° (як сума кутів трикутника). Звідси ∠L = 180° – (70° + 40°) = 180° – 110° = 70°.

Відповідь: 70°, 70°, 40°.

454. 1)

Зовнішній кут трикутника та його властивості

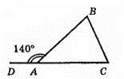
Нехай? ABC – даний трикутник, ∠BAD = 140°. Нехай ∠B = ч, тоді ∠C = х + 30°. За властивістю зовнішнього кута трикутника: ∠ВАО = ∠B + ∠C. Складемо рівняння: х + х + 30° = 140°; 2х = 110°; х = 55°. Отже, ∠B = 55°, ∠C = 55° + 30° = 85°.

Відповідь: 55°, 85°.

2) Нехай? ABC – даний трикутник, ∠BAD = 140°, ∠B = х, тоді ∠С = 4х. За властивістю зовнішнього кута трикутника маємо: ∠BAD = ∠B + ∠С. Складемо рівняння: х + 4х = 140°; 5х = 140°; х =28°. Отже, ∠B = 28°, ∠C = 28° x 4 = 112°.

Відповідь: 28°, 112°.

455. 1)

Зовнішній кут трикутника та його властивості

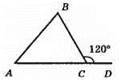
Нехай? ABC – даний трикутник, ∠BCD = 120°, ∠А = х, тоді ∠В = х + 20°. За властивістю зовнішнього кута трикутника маємо: ∠BCD = ∠А + ∠B. Складемо рівняння: х + х + 20° = 120°; 2х =100°; х = 50°. Отже, ∠А = 50°, ∠B = 50° + 20° = 70°.

Відповідь: 50°, 70°.

2) Нехай? ABC – даний трикутник, ∠А = х, ∠B = 3х. За властивістю зовнішнього кута трикутника маємо: ∠BCD = ∠А + ∠B. Складемо рівняння: х + 3х = 120°; 4х = 120°; х = 30°. Отже, ∠А =30°, ∠B = 3 х 30° = 90°.

Відповідь: 30°, 90°.

456. І випадок.

Зовнішній кут трикутника та його властивості

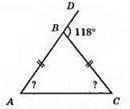
Зовнішній кут при вершині трикутника. Нехай? ABC – даний рівнобедрений трикутник (AB = ВС), ∠А = ∠С. За властивістю зовнішнього кута трикутника: ∠DBC = ∠А + ∠С = 118°, ∠А = ∠С = 118° : 2 = 59°. ∠АВС = 180° – ∠DBC = 180° – 118° = 62°.

Відповідь: 62°, 59°, 59°.

II випадок.

Зовнішній кут трикутника та його властивості

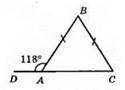
Зовнішній кут при основі трикутника. Нехай? ABC – даний рівнобедрений трикутник (ВА = ВС). ∠DAB і ∠BAC – суміжні, їх сума дорівнює 180°. ∠BAC = 180° – 118° = 62°. Оскільки ∠BAC = ∠ВСА (як кути при основі рівнобедреного трикутника), то ∠ВСА = 62°. ∠А + ∠B + ∠C = 180°, ∠В = 180° – (∠A + ∠C) = 180° – 124° = 56°.

Відповідь: 62°, 62°, 54°.

457.

Зовнішній кут трикутника та його властивості

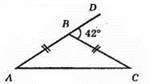
I випадок. Зовнішній кут при вершині. Нехай? АВС даний рівнобедрений трикутник (AB = ВС). ∠А = ∠С (як кути в основі рівнобедреного трикутника). ∠BDC = ∠А + ∠С за властивістю зовнішнього кута трикутника. 42° = ∠А + ∠С, звідси ∠А = ∠С = 42° : 2 = 21°. ∠B = 180° – 42° = 138°.

Відповідь: 21°, 21°, 138°.

II випадок. Зовнішній кут при основі. Цей випадок неможливий, бо тоді кути в основі будуть тупими, а у трикутнику можливий тільки один тупий кут.

458.

Зовнішній кут трикутника та його властивості

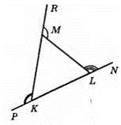
Нехай? KNL – даний трикутник. За властивістю зовнішнього кута трикутника маємо: ∠RML = ∠K + ∠L, ∠MLN = ∠K + ∠M, ∠PKM = ∠M + ∠L. Додамо рівності ∠RML + ∠MLN = ∠PKM = ∠K + ∠L + ∠K +∠M + ∠M + ∠L = 2 (∠K + ∠M + ∠L) = 2 x 180° = 360°. Отже, сума зовнішніх кутів будь-якого трикутника, взятих по одному при кожній вершині, дорівнює 360°.

459. Нехай 3х, 5х і 4х – градусні міри зовнішніх кутів трикутника. Оскільки сума зовнішніх кутів трикутника, взятих по одному при кожній вершині, дорівнює 360°, складемо рівняння: 3х + 5х + 4х = 360°; 12х = 360°; х = 30°. Таким чином, зовнішні кути трикутника дорівнюють 3 х 30° = 90°, 5 х 30° = 150°, 4 x 30° = 120°.

Знайдемо кути трикутника. Оскільки зовнішні кути трикутника суміжні з кутами трикутника, то вони відповідно дорівнюють 90°, 30°, 60° і відносяться як 3:1:2.

Відповідь: 3:1:2.

460.

Зовнішній кут трикутника та його властивості

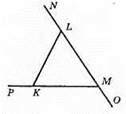
Нехай градусні міри кутів трикутника ∠K = 7x, ∠L = 3х, ∠M = 9х. Оскільки зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів, не суміжних з ним, маємо: ∠NLK = ∠K + ∠M = 7х + 9х = 16х. ∠PKL = ∠L + ∠M = 8х + 9х = 11х. ∠OMK = ∠K + ∠L = 7x + 8x = 15х. Отже, відношення зовнішніх кутів 17:16:15.

Відповідь: 17:16:15.

461.

Зовнішній кут трикутника та його властивості

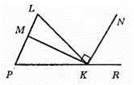
Нехай? РLK – даний трикутник. ∠PKL і ∠LKR – суміжні. КМ – бісектриса кута LKP. ∠PKM = ∠LKM.

KN – бісектриса ∠LKR, ∠LKN = ∠NKR. ∠PKL + ∠LKR = 180°, ∠PKM + ∠LKM + ∠LKN + ∠NKR = 180°, 2∠LKM + 2∠LKN = 180°, 2(∠LKM + ∠LKN) = 180°, ∠LKM + ∠LKN = 90°. Отже, KM ⊥ KN.

462.

Зовнішній кут трикутника та його властивості

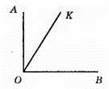
Нехай OK – промінь, що проходить між сторонами ∠AOB, ∠AOK = х, ∠KOB = 90° – х. ∠KOB – ∠AOK = (90° – х) – х = 90° – 2х. ∠AOK + ∠KOB = 90°, 1/3(∠AOK + ∠KOB) = 30°. Отже, 90° – 2x = 30°, 2x = 60°, x = 30°. ∠AOK = 30°, ∠KOB = 90° – 30° = 60°.

Відповідь: 30°, 60°.

463. Зовнішній кут трикутника та його властивості

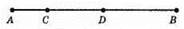
Нехай AB = 22,8 см, AC = x см, CD = 2x см, DB = (2x + 1,8) см.

Маємо рівняння: x + 2x + 2x + 1,8 – 22,8; 5x = 21; x = 4,2. Отже, AC = 4,2 см, CD = 8,4 см, DB = 10,2 см.

Відповідь: 4,2 см, 8,4 см, 10,2 см.

464.

Зовнішній кут трикутника та його властивості


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Властивості кутів трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 10. Властивості кутів трикутника 344. ∠E = 60°, ∠F = 40°, ∠D = 80°. ∠E + ∠F + ∠D = 60° + 40° + 80° = 180°. 345. На мал. 208 неправильно сказано градусну міру кутів? АВС, оскільки? ABC – прямокутний, a ∠B + ∠C = […]...

  2. Властивості й ознака рівнобедреного трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 12. Властивості й ознака рівнобедреного трикутника 476. На мал. 72: ML і МК – бічні сторони, KL – основа, ∠K = ∠L. 477. KD = DF, КЕ = EF, ∠K = ∠F, ∠KDE = ∠FDE, ∠DEK = ∠DEF = 90°. 478. Щоб провести бісектрису, медіану і […]...

  3. Сума кутів трикутника. Нерівність трикутника § 3. Паралельні прямі. Сума кутів трикутника § 15. Сума кутів трикутника. Нерівність трикутника Вправи 357. Нехай х° – третій кут трикутника, тоді 35 + 96 + х = 180, звідси х + 131 = 180; х = 180 – 131; х = 49. Отже, третій кут дорівнює 49°. Відповідь: 49°. 358. Нехай х° – […]...

  4. Властивості прямокутного трикутника § 3. Паралельні прямі. Сума кутів трикутника § 17. Властивості прямокутного трикутника 457. Найбільший катет трикутника дорівнює 24 см. 458. ?DEF – прямокутний, ∠F = 90°, ∠D = 30°, DE = 18 см. Відповідь: 9 см. 459. ?KCM – прямокутний, ∠M = 90°, ∠C = 60°, MC = 7 см. ∠MKC = 90° – 60° […]...

  5. Сума кутів трикутника Геометрія Основні властивості найпростіших геометричних фігур Сума кутів трикутника Теорема. Сума кутів трикутника дорівнює . Із цієї теореми випливають наслідки: 1. У будь-якому трикутнику принаймні два кути гострі (тобто в трикутнику не може бути більше одного прямого або тупого ­кута). 2. Кути рівностороннього трикутника дорівнюють . Зовнішнім кутом трикутника при даній вершині називається кут, суміжний […]...

  6. Рівні трикутники. Висота, медіана, бісектриса трикутника § 2. Трикутники 6. Рівні трикутники. Висота, медіана, бісектриса трикутника Практичні завдання 132. 133. ВН – спільна висота трикутників ABD, ABC, BDC. ВН лежить поза трикутником BCD. 134. 135. 136. Вправи 137. 1) ME; 2) ∠E; 3) MK i KE; 4) ∠K i ∠E. 138. 1) ∠E; 2) ∠C i ∠E;3) CF; 4) CF і […]...

  7. Описане та вписане коло трикутника § 3. Паралельні прямі. Сума кутів трикутника § 20. Описане та вписане коло трикутника 540. 1) Різносторонній гострокутний трикутник. 2) Прямокутний трикутник. 3) Тупокутний трикутник. 541. 1) Рівнобедрений гострокутний трикутник. 2) Рівнобедрений тупокутний трикутник. 542. 543. 544. Вправи 545. Медіана BD рівнобедреного трикутника ABC є в той же час і серединним перпендикуляром до сторони АС […]...

  8. Рівнобедрений трикутник і його властивості § 2. Трикутники 8. Рівнобедрений трикутник і його властивості Практичні завдання 196. 197. 198. Вправи 199. 1) Р = 13 + 2 х 8 = 29(см). Відповідь: 29 см. 2) Нехай х см – бічна сторона, тоді 15 + 2х = 39, тоді 2х = 39 – 15; 2х = 24; х = 24 : […]...

  9. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 19. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників 466. 1) PF – гіпотенуза, PL і LF – катети. 2) PF довша за PL, PF довша за LF, оскільки PF – гіпотенуза. 467. На рис. 321 трикутники рівні за двома катетами. Оскільки АС = ML, СВ = LP, […]...

  10. Дотична до кола, її властивості Розділ 4. Коло і круг. Геометричні побудови § 22. Дотична до кола, її властивості 607. Проведемо радіус ОР, а потім за допомогою косинця побудуємо пряму m, перпендикулярну до радіуса. За теоремою 2 пряма m є дотичною до кола. 608. Проведемо радіус ОМ, а потім за допомогою косинця побудуємо пряму n, перпендикулярну до радіуса. За теоремою […]...

  11. Трикутник і його елементи Розділ 1. Найпростіші геометричні фігури та їх властивості § 9. Трикутник і його елементи 292. На мал. 194 зображені трикутники ABD, ABC, ОВС. Проти кута C в трикутнику АВС лежить сторона АB, в трикутнику DBC – сторона BD. Прилеглими до кута С в трикутнику ABC є сторони АС і ВС, в трикутнику DBC – сторони […]...

  12. Ознаки паралельності прямих. Сума кутів трикутника Урок № 40 Тема. Ознаки паралельності прямих. Сума кутів трикутника Мета: перевірити рівень засвоєння знань та вмінь, передбачених програмою, із зазначених тем. Тип уроку: контроль та корекція знань. ХІД УРОКУ I. Організаційний момент II. Перевірка домашнього завдання Зібрати зошити з виконаною домашньою контрольною роботою. Роботу оцінити та врахувати в тематичному балі. III. Умова контрольної роботи […]...

  13. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника Розділ 3. Трикутники. Ознаки рівності трикутників § 15. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника 351. 1) AT – висота трикутника ABC. 2) AN – медіана трикутника ABC. 3) АР – бісектриса трикутника? AВС. 352. Оскільки AK – висота, то ∠BKA = ∠CKA = 90°. 353. Оскільки АК – бісектриса, то ∠BAK = […]...

  14. Вправи 425-474 425. АС – основа; AB = CB; ∠ADC = 150°. ∠CAD = ∠BAD = x; ∠ACD = 2x; x + 2x + 150° = 180°; 3x = 180° – 150°; 3x = 30°; x = 10°; ∠C = ∠A = 20°; ∠B = 180° – (20° + 20°) = 140°. Відповідь: 20°, 20°, 140°. 426. […]...

  15. СУМА КУТІВ ТРИКУТНИКА РОЗДІЛ 3 ТРИКУТНИКИ & 10. СУМА КУТІВ ТРИКУТНИКА Теорема 8 Сума кутів трикутника дорівняй: 180°. Доведення. Нехай ABC – довільний трикутник (мал. 130). Через йот вершину С проведемо пряму КР, паралельну стороні АВ. Утворені кути АСК і ВСР позначимо цифрами 1 і 2. Тоді ∠A = ∠1, ∠B = ∠2, як внутрішні різносторонні кути при […]...

  16. Сума кутів трикутника Урок № 34 Тема. Сума кутів трикутника Мета: закріпити знання учнів про зміст теореми про суму кутів трикутника та наслідків з неї; працювати над засвоєнням поняття “зовнішній кут трикутника”; розглянути властивість зовнішнього кута трикутника. Сформувати вміння: – знаходити на рисунку та виконувати зображення зовнішнього кута при даній вершині трикутника; – записувати теорему про зовнішній кут […]...

  17. Ознаки рівнобедреного трикутника § 2. Трикутники 9. Ознаки рівнобедреного трикутника 232. ?ABC – рівнобедрений, тому ВК є бісектрисою кута ABC, отже, ∠ABC = 2 х ∠ABK = 2 x 25° = 50°. Відповідь: 50°. 233. BK є висотою та медіаною, тому? ABC – рівнобедрений, AB = ВС, отже, ∠C = ∠A =17°. Відповідь: 17°. 234. AС = ВС, […]...

  18. НЕРІВНОСТІ ТРИКУТНИКА РОЗДІЛ 3 ТРИКУТНИКИ & 15. НЕРІВНОСТІ ТРИКУТНИКА Ви вже знаєте, що кожна сторона трикутника менша від суми двох інших його сторін. Щоб довести це твердження як теорему, спочатку розглянемо іншу теорему. Теорема 19 У кожному трикутнику проти більшої сторони лежить більший кут, а проти більшого кута – більша сторона. Доведення. 1) Нехай у трикутнику ABC […]...

  19. Властивості конуса 1. 1) Твірна конуса не може утворювати з його основою прямий кут, оскільки Вона є гіпотенузою трикутника обертання, яка утворює бічну поверхню конуса. 2) Теж не може (обгрунтування у п. 1). Якщо конус зрізаний 1) ні; 2) так. Відповідь: 1) ні; 2) ні для зрізаного конуса 1) ні, 2) так. 2. Нехай SA – твірна […]...

  20. Знаходження площі трикутника за двома сторонами і кутом між ними УРОК № 12 Тема. Знаходження площі трикутника за двома сторонами і кутом між ними Мета уроку: виведення формули для знаходження площі трикутника за двома сторонами і кутом між ними. Формування вмінь застосовувати виведену формулу до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника”[13]. Вимоги до рівня підготовки учнів: […]...

  21. Взаємне розміщення двох кіл Розділ 4. Коло і круг. Геометричні побудови § 25. Взаємне розміщення двох кіл 656. На рис. 404 кола перетинаються. На рис. 405 кола дотикаються. На рис. 406 кола не мають спільних точок. 657. 1) Кола мають внутрішній дотик. 2) Кола перетинаються. 3) Кола концентричні. 658. 1) Кола мають зовнішній дотик. 2) Кола не перетинаються. 659. […]...

  22. Співвідношення між сторонами й кутом прямокутного трикутника Геометрія Трикутники Співвідношення між сторонами й кутом прямокутного трикутника Нехай ABC – прямокутний трикутник з прямим кутом С і гострим кутом при вершині A, що дорівнює . Косинусом гострого кута прямокутного трикутника називається відношення при­лег­лого катета до гіпотенузи. На рисунку або . Синусом кута називається відношення протилежного катета до гіпотенузи: або . Тангенсом кута називається […]...

  23. Кут. Вимірювання кутів. Бісектриса кута Розділ 1. Елементарні геометричні фігури та їхні властивості § 3. Кут. Вимірювання кутів. Бісектриса кута 33. 1) М – вершина кута, МА і МК – сторони кута АМК; 2) L – вершина кута, LP і LF – сторони кута PLF; 3) N – вершина кута, NB i NC – сторони кута BNC. 34. 1) O […]...

  24. Середня лінія трикутника Геометрія Трикутники Середня лінія трикутника Середньою лінією трикутника називається відрізок, який сполучає середини двох його сторін. Теорема 1. Середня лінія трикутника, яка сполучає середини двох його сторін, паралельна третій стороні й дорівнює її половині. На рисунку праворуч: ;. У трикутнику можна провести три середні лінії. Вони утворюють трикутник з такими ж кутами, як даний, і […]...

  25. Кути трикутника і чотирикутника Урок № 50 Тема: Кути трикутника і чотирикутника Мета. Познайомити учнів з видами кутів і трикутників в залежності від кутів, які входять до кута. Навчити учнів вимірювати кути за допомогою транспортира. Формувати уміння і навички розв’язувати геометричні задачі. Розвивати логічне мислення учнів, шляхом розв’язування задач, продовжувати формувати вміння працювати з підручником. Форми роботи: бліцопитування, робота […]...

  26. Властивості кола. Дотична до кола § 3. Паралельні прямі. Сума кутів трикутника § 19. Властивості кола. Дотична до кола Практичні завдання 507. АК = КВ. 508. AB ⊥ CD – дотичні до кола. 509. АС i ВС – дотичні до кола. 510. Таких кіл може бути два. Вправи 511. CD ⊥ AB. ?АОК = ?ВОК (за катетом і гіпотенузою: ОК […]...

  27. Порівняння сторін і кутів трикутника Урок № 37 Тема. Порівняння сторін і кутів трикутника Мета: перевірити рівень засвоєння навчального матеріалу теми “Прямокутні трикутники”; домогтися засвоєння учнями змісту та схеми доведення теореми про співвідношення між сторонами і кутами трикутника; сформувати вміння відтворювати формулювання теореми про співвідношення між сторонами і кутами трикутника та використовувати це співвідношення під час розв’язування задач. Тип уроку: […]...

  28. Висота, бісектриса, медіана трикутника Геометрія Основні властивості найпростіших геометричних фігур Висота, бісектриса, медіана трикутника Висотою Трикутника, опущеною з да­ної вершини, називається перпендикуляр, проведений із цієї вершини до прямої, що містить протилежну сторону трикутника. У кожному трикутнику можна провести три висоти. Висоти трикутника (або прямі, що їх містять) перетинаються в одній точці. На рисунках зображено, як перетинаються висоти в гострокутному […]...

  29. Кути трикутника і чотирикутника. Розв’язання задач Урок № 51 Тема. Кути трикутника і чотирикутника. Розв’язання задач Мета. Продовжити формування в учнів. вміння розв’язувати задачі геометричного змісту, повторити основні поняття теми, сприяти формуванню практичних навичок при виконанні вправ. Форми роботи: фронтальна бесіда, індивідуальна робота біля дошки, виконання тренувальних вправ, робота з підручником. Обладнання: лінійка, транспортир, кольорова крейда, косинець, таблиці. Тип уроку: урок […]...

  30. Ознаки рівнобедреного трикутника Геометрія Основні властивості найпростіших геометричних фігур Ознаки рівнобедреного трикутника Теорема 1. Якщо в трикутнику два кути рівні, то він рівнобедрений. Теорема 2. Трикутник рівнобедрений, ­якщо: – одна з його висот є медіаною; – одна з його медіан є бісектрисою; – одна з його висот є бісектрисою. Теорема 3. Трикутник рівнобедрений, ­якщо: – дві його висоти […]...

  31. Площа трикутника Геометрія Площі фігур Площа трикутника , де h – висота, a – сторона, до якої проведена ця висота. Оскільки , то . Висоти трикутника обернено пропорційні сторонам, на які вони опущені. Зверніть увагу: більшій стороні трикутника відповідає менша висота, і навпаки. , , де P – периметр трикутника, r – радіус вписаного кола. , , […]...

  32. Вертикальні кути. Кут між двома прямими, що перетинаються Розділ 2. Взаємне розміщення прямих па площині § 6. Вертикальні кути. Кут між двома прямими, що перетинаються 107. 1) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 15°, дорівнює 15°. 2) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 129°, дорівнює 129°. Відповідь: 1) 15°; […]...

  33. Вправи 375-424 375. ВС – бісектриса ∠ABD; ∠ABD = 80° + 80° = 160°; ∠BAC + ∠ABD = 20° + 160° = 180°; ∠BAC і ∠ABD – внутрішні односторонні кути при прямих АС і BD та січній АВ. Отже, BD || АС. 376. ∠A = 70°, ∠B = 40°, BE – бісектриса ∠ABD; ∠DBE = ∠ABE = […]...

  34. ТРИКУТНИК. СТОРОНА, ВЕРШИНА, КУТ ТРИКУТНИКА. ПОРІВНЯННЯ ПРЕДМЕТІВ (“НАЙДОВШИЙ ОЗНАКИ І ВЛАСТИВОСТІ ПРЕДМЕТІВ. МНОЖИНИ. ГЕОМЕТРИЧНІ ФІГУРИ. НАТУРАЛЬНІ ЧИСЛА 1-10 І ЧИСЛО 0 Урок 12. ТРИКУТНИК. СТОРОНА, ВЕРШИНА, КУТ ТРИКУТНИКА. ПОРІВНЯННЯ ПРЕДМЕТІВ (“НАЙДОВШИЙ – НАЙКОРОТШИЙ”, “ОДНАКОВІ ЗА ДОВЖИНОЮ”) Мета: ознайомити учнів із трикутником, його елементами; вчити порівнювати предмети (“найдовший – найкоротший”, “однакові за довжиною”); розвивати мислення; виховувати старанність. Хід уроку І. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. ПОВТОРЕННЯ […]...

  35. Знаходження площі трикутника за радіусом вписаного та описаного кіл УРОК № 14 Тема. Знаходження площі трикутника за радіусом вписаного та описаного кіл Мета уроку: виведення формул для знаходження площі трикутника за радіусом вписаного та описаного кіл. Формування вмінь учнів застосовувати виведені формули до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Площі трикутників і чотирикутників” [13], посібник [14]. Вимоги до рівня підготовки учнів: […]...

  36. Медіана, бісектриса і висота трикутника Урок № 24 Тема. Медіана, бісектриса і висота трикутника Мета: домогтися засвоєння учнями: – змісту понять “медіана трикутника”; “бісектриса трикутника”; “висота трикутника”; – уявлення про положення висот у різних видах трикутника. Сформувати вміння: – зображати медіани, висоти та бісектриси трикутника; – розрізняти ці відрізки, виходячи з умови задачі. Тип уроку: застосування знань, умінь та навичок. […]...

  37. РОЗВ’ЯЗУВАННЯ ЗАДАЧ НА ВИВЧЕНІ ВИПАДКИ АРИФМЕТИЧНИХ ДІЙ. ЗНАХОДЖЕННЯ ЗНАЧЕНЬ ВИРАЗІВ. ОБЧИСЛЕННЯ ДОВЖИНИ СТОРОНИ РІВНОСТОРОННЬОГО ТРИКУТНИКА ЗА ЙОГО ПЕРИМЕТРОМ АРИФМЕТИЧНІ ДІЇ МНОЖЕННЯ ТА ДІЛЕННЯ (продовження) Урок 74. РОЗВ’ЯЗУВАННЯ ЗАДАЧ НА ВИВЧЕНІ ВИПАДКИ АРИФМЕТИЧНИХ ДІЙ. ЗНАХОДЖЕННЯ ЗНАЧЕНЬ ВИРАЗІВ. ОБЧИСЛЕННЯ ДОВЖИНИ СТОРОНИ РІВНОСТОРОННЬОГО ТРИКУТНИКА ЗА ЙОГО ПЕРИМЕТРОМ Мета: формувати поняття про таблицю множення і ділення на 3; тренувати здатність множити і ділити на 2 і 3; навчити обчислювати довжину сторони рівностороннього трикутника за його периметром; розвивати […]...

  38. Властивість медіани, бісектриси й висоти рівнобедреного трикутника Урок № 25 Тема. Властивість медіани, бісектриси й висоти рівнобедреного трикутника Мета: домогтися свідомого сприйняття учнями змісту теореми про властивість медіани, бісектриси й висоти рівнобедреного трикутника та наслідків з неї; сформувати вміння відтворювати названі властивості та застосовувати їх під час розв’язування задач. Тип уроку: засвоєння знань, умінь та навичок. Наочність і обладнання: набір демонстраційного креслярського […]...

  39. РІВНОБЕДРЕНИЙ ТРИКУТНИК РОЗДІЛ 3 ТРИКУТНИКИ & 13. РІВНОБЕДРЕНИЙ ТРИКУТНИК Трикутник називають рівнобедреним, якщо в нього дві сторони рівні. Рівні сторони рівнобедреного трикутника навивають бічними сторонами, а третю його сторону – основою. Трикутник, який не є рівнобедреним, називають різностороннім. Трикутник, у якого всі сторони рівні, називають рівностороннім. Рівносторонній трикутник є окремим видом рівнобедреного трикутника (мал. 166). Рівнобедрений трикутник […]...

  40. Зовнішній борг держави Зовнішній борг держави – заборгованість держави іноземним громадянам, фірмам і установам. Має місце тоді, коли борг перевищує доходи тієї чи іншої країни. Зовнішній борг збільшується, коли утворюється дефіцит платіжного балансу, і навпаки, активне сальдо платіжного балансу його зменшує. Зовнішній борг держави особливо зростає при дефіциті торгового балансу країни Коли обсягів експорту бракує для оплати імпорту, […]...

Ви зараз читаєте: Зовнішній кут трикутника та його властивості
«
»