Головна ⇒ 📌Довідник з геометрії ⇒ Бісектриса
Бісектриса
Геометрія
Основні властивості найпростіших геометричних фігур
Бісектриса
Бісектрисою кута називається промінь, який виходить із вершини кута, проходить між його сторонами й ділить кут пополам.
На рисунку BD – бісектриса 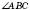 .
.
Властивості бісектриси
Теорема 1. Бісектриса кута утворює з його сторонами кути, не більші за 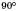 .
.
Теорема 2. Бісектриси вертикальних кутів лежать на одній прямій (тобто є доповняльними півпрямими).
Теорема 3. Бісектриси суміжних кутів утворюють прямий кут.
Теорема 4. Бісектриса розгорнутого кута утворює прямий кут з його стороною.
Related posts:
- Суміжні й вертикальні кути Геометрія Основні властивості найпростіших геометричних фігур Суміжні й вертикальні кути Два кути називаються Суміжними, якщо в них одна сторона спільна, а інші сторони є доповняльними півпрямими. На рисунку і – суміжні. Властивості суміжних кутів Теорема 1. Сума суміжних кутів дорівнює . (Зверніть увагу: кути, сума яких дорівнює , не обов’язково суміжні.) Теорема 2. Коли два […]...
- Кут. Вимірювання кутів. Бісектриса кута Розділ 1. Елементарні геометричні фігури та їхні властивості § 3. Кут. Вимірювання кутів. Бісектриса кута 33. 1) М – вершина кута, МА і МК – сторони кута АМК; 2) L – вершина кута, LP і LF – сторони кута PLF; 3) N – вершина кута, NB i NC – сторони кута BNC. 34. 1) O […]...
- Вертикальні кути Розділ 1. Найпростіші геометричні фігури та їх властивості § 5. Вертикальні кути 152. 1) ∠AYX і ∠BYZ – вертикальні; 2) ∠OLK і ∠MLN – не вертикальні. 153. 1) ∠AOD – вертикальний з кутом 1; 2) ∠АОС і ∠DOB – суміжні з кутом 1. 154. ∠BOA і ∠COD – суміжні. ∠BOA = ∠COD = 60°. 155. […]...
- Вертикальні кути. Кут між двома прямими, що перетинаються Розділ 2. Взаємне розміщення прямих па площині § 6. Вертикальні кути. Кут між двома прямими, що перетинаються 107. 1) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 15°, дорівнює 15°. 2) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 129°, дорівнює 129°. Відповідь: 1) 15°; […]...
- Вправи 150-175 150. ∠1 = 90°, ∠2 = ∠1 = 90° – вертикальні кути; ∠3 – суміжний куту ∠1. ∠3 = 180° – 90° = 90°, ∠3 = ∠4 = 90° (вертикальні кути). 151. ∠(ac) = 70°; ∠(ab) = 90°; ∠(bc) = 90° – ∠(ac) = 90° – 70° = 20°. 152. а ⊥ с; ∠(ab) = […]...
- Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої Розділ 2. Взаємне розміщення прямих па площині § 7. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої 128. m ⊥ n, MN ⊥ АВ. 129. KA ⊥ c, ВМ ⊥ с. 130. ВL ⊥ a. MВ ⊥ a. 131. 1) Відрізки AB і MN перпендикулярні, оскільки вони лежать на перпендикулярних прямих a і b. 2) […]...
- Висота, бісектриса, медіана трикутника Геометрія Основні властивості найпростіших геометричних фігур Висота, бісектриса, медіана трикутника Висотою Трикутника, опущеною з даної вершини, називається перпендикуляр, проведений із цієї вершини до прямої, що містить протилежну сторону трикутника. У кожному трикутнику можна провести три висоти. Висоти трикутника (або прямі, що їх містять) перетинаються в одній точці. На рисунках зображено, як перетинаються висоти в гострокутному […]...
- Сума кутів трикутника Геометрія Основні властивості найпростіших геометричних фігур Сума кутів трикутника Теорема. Сума кутів трикутника дорівнює . Із цієї теореми випливають наслідки: 1. У будь-якому трикутнику принаймні два кути гострі (тобто в трикутнику не може бути більше одного прямого або тупого кута). 2. Кути рівностороннього трикутника дорівнюють . Зовнішнім кутом трикутника при даній вершині називається кут, суміжний […]...
- Промінь. Кут. Вимірювання кутів § 1. Найпростіші геометричні фігури та їхні властивості 3. Промінь. Кут. Вимірювання кутів Практичні завдання 49. Промені AB і АС – не доповняльні. Промінь AN – доповняльний до променя AB, а промінь AM – доповняльний до променя АС. На рисунку зображено промені АB, АС, AN, AM. 50. Промені AB і ВА не е доповняльними, оскільки […]...
- Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника Розділ 3. Трикутники. Ознаки рівності трикутників § 15. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника 351. 1) AT – висота трикутника ABC. 2) AN – медіана трикутника ABC. 3) АР – бісектриса трикутника? AВС. 352. Оскільки AK – висота, то ∠BKA = ∠CKA = 90°. 353. Оскільки АК – бісектриса, то ∠BAK = […]...
- Суміжні та вертикальні кути § 1. Найпростіші геометричні фігури та їхні властивості § 4. Суміжні та вертикальні кути Практичні завдання 86. ∠BAC – гострий, ∠OAB – суміжний до кута ВАС. ∠АОВ – прямий, ∠COA – суміжний до кута АОВ. ∠BOC – тупий, ∠AOB – суміжний до кута ВОС. 87. ∠AOC і ∠COB – суміжні. 88. а) ∠ABD i ∠CBD; […]...
- Суміжні кути Урок № 10 Тема. Суміжні кути Мета: домогтися розуміння учнями змісту наслідків з теореми про суму суміжних кутів та змісту понять “наслідок”, “посилання”; використовуючи знання теореми про суміжні кути та її наслідки, виробити вміння розв’язувати задачі на обчислення та доведення, в яких йдеться про суміжні кути. Тип уроку: застосування знань, умінь та навичок. Наочність і […]...
- Медіана, бісектриса і висота трикутника Урок № 24 Тема. Медіана, бісектриса і висота трикутника Мета: домогтися засвоєння учнями: – змісту понять “медіана трикутника”; “бісектриса трикутника”; “висота трикутника”; – уявлення про положення висот у різних видах трикутника. Сформувати вміння: – зображати медіани, висоти та бісектриси трикутника; – розрізняти ці відрізки, виходячи з умови задачі. Тип уроку: застосування знань, умінь та навичок. […]...
- Найпростіші геометричні фігури та їх властивості Урок № 14 Тема. Найпростіші геометричні фігури та їх властивості Мета: перевірити та оцінити рівень засвоєння знань та вмінь учнів з теми, передбачених програмою; виявити прогалини в знаннях та вміннях учнів для подальшого їх усунення. Тип уроку: перевірка та корекція знань, навичок та вмінь. ХІД УРОКУ І. Умова тематичної контрольної роботи Варіант 1 Початковий рівень […]...
- Тригранний і многогранний кути Геометрія Многогранники Тригранний і многогранний кути Нехай промені a, b, c виходять з однієї точки й не лежать в одній площині. Тригранним кутом називається фігура, яка складається з трьох плоских кутів , , (див. рисунок). Ці кути називаються Гранями тригранного кута, а їх сторони – Ребрами. Спільна вершина плоских кутів називається Вершиною тригранного кута. Двогранні […]...
- Вправи для повторення до розділу 2 Розділ 2. Взаємне розміщення прямих па площині Вправи для повторення до розділу 2 До § 5. 226. На рис. 184 суміжні кути ∠2 і ∠3. на рис. 185 суміжні кути ∠1 і ∠4 та ∠2 i ∠3. На рис. 186 суміжні кути ∠1 і ∠2 та ∠3 i ∠4. 227. 1) Так, можна. Треба побудувати […]...
- Паралелограм Геометрія Чотирикутники Чотирикутником називається фігура, яка складається з чотирьох точок і чотирьох відрізків, що послідовно їх сполучають. При цьому жодні три з даних точок не повинні лежати на одній прямій, а відрізки, які їх сполучають, не повинні перетинатися. Дані точки називаються Вершинами чотирикутника, а відрізки, що їх сполучають,- Сторонами чотирикутника. Вершини чотирикутника називаються Сусідніми, якщо […]...
- Рівнобедрений трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівнобедрений трикутник Трикутник називається Рівнобедреним, якщо у нього дві сторони рівні. Ці сторони називаються Бічними сторонами, а третя сторона – Основою трикутника. На рисунку: ABC – рівнобедрений трикутник; – бічні сторони; AC – основа. Теорема 1. У рівнобедреному трикутнику кути при основі є рівними. Теорема 2. У рівнобедреному трикутнику […]...
- Властивості кутів трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 10. Властивості кутів трикутника 344. ∠E = 60°, ∠F = 40°, ∠D = 80°. ∠E + ∠F + ∠D = 60° + 40° + 80° = 180°. 345. На мал. 208 неправильно сказано градусну міру кутів? АВС, оскільки? ABC – прямокутний, a ∠B + ∠C = […]...
- СУМІЖНІ І ВЕРТИКАЛЬНІ КУТИ Геометрія Евкліда є лише першим кроком до вивчення форм реального простору. О. Смогоржевський РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ У цьому розділі підручника ви розширите і поглибите свої знання про прямі і промені однієї площини, ознайомитеся з дуже важливими поняттями: суміжні кути, вертикальні кути, перпендикулярні прямі, паралельні прямі тощо, а також із важливими загальноматематичними […]...
- Вправи 475-524 475. ?ABC – прямокутний; ∠A = 30°; АС = 18 см; ВК – бісектриса, проведена до катета АС; ∠CBK = ∠ABK = ∠CBA : 2 = 60° : 2 = 30°; ∠CBA = 90° – ∠CAB = 90° – 30° = 60°; СК = х, тоді AK = 18 – х. ?АВК – прямокутний; ∠A […]...
- Кути, вписані в коло Геометрія Кути, пов’язані з колом Кути, вписані в коло Кут розбиває площину на дві частини. Кожна із цих частин називається Плоским кутом. Плоскі кути із спільними сторонами називаються Доповняльними. Якщо плоский кут є частиною півплощини, то його градусною мірою називається градусна міра звичайного кута з тими самими сторонами. Центральним кутом у колі називається плоский кут […]...
- Вправи 100-49 100. А || b, с || d. 4 точки перетину. 101. 1) Всі чотири прямі перетинають пряму с. 2) Одна пряма паралельна, три перетинають пряму с. 102. 1) m || с; 2) m || b; в) m || а. 103. а || b. Якщо b i c не перетинаються, то через т. М проведено 2 […]...
- Вимірювання кутів. Види кутів УРОК 36 Тема. Види кутів. Вимірювання кутів Мета: систематизувати знання учнів про поняття кута, його елементів, позначення, вимірювання і класифікацію; вдосконалювати вміння і відпрацьовувати навички вимірювання кутів, визначати видів кутів і розв’язувати задачі на застосування аксіоми вимірювання кутів. Тип уроку: застосовування знань, вмінь та навичок. Обладнання: таблиця “Кути. Вимірювання кутів”. Хід уроку I. Перевірка домашнього […]...
- РІВНОБЕДРЕНИЙ ТРИКУТНИК РОЗДІЛ 3 ТРИКУТНИКИ & 13. РІВНОБЕДРЕНИЙ ТРИКУТНИК Трикутник називають рівнобедреним, якщо в нього дві сторони рівні. Рівні сторони рівнобедреного трикутника навивають бічними сторонами, а третю його сторону – основою. Трикутник, який не є рівнобедреним, називають різностороннім. Трикутник, у якого всі сторони рівні, називають рівностороннім. Рівносторонній трикутник є окремим видом рівнобедреного трикутника (мал. 166). Рівнобедрений трикутник […]...
- Рівні трикутники. Висота, медіана, бісектриса трикутника § 2. Трикутники 6. Рівні трикутники. Висота, медіана, бісектриса трикутника Практичні завдання 132. 133. ВН – спільна висота трикутників ABD, ABC, BDC. ВН лежить поза трикутником BCD. 134. 135. 136. Вправи 137. 1) ME; 2) ∠E; 3) MK i KE; 4) ∠K i ∠E. 138. 1) ∠E; 2) ∠C i ∠E;3) CF; 4) CF і […]...
- Властивості й ознака рівнобедреного трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 12. Властивості й ознака рівнобедреного трикутника 476. На мал. 72: ML і МК – бічні сторони, KL – основа, ∠K = ∠L. 477. KD = DF, КЕ = EF, ∠K = ∠F, ∠KDE = ∠FDE, ∠DEK = ∠DEF = 90°. 478. Щоб провести бісектрису, медіану і […]...
- Описане та вписане коло трикутника § 3. Паралельні прямі. Сума кутів трикутника § 20. Описане та вписане коло трикутника 540. 1) Різносторонній гострокутний трикутник. 2) Прямокутний трикутник. 3) Тупокутний трикутник. 541. 1) Рівнобедрений гострокутний трикутник. 2) Рівнобедрений тупокутний трикутник. 542. 543. 544. Вправи 545. Медіана BD рівнобедреного трикутника ABC є в той же час і серединним перпендикуляром до сторони АС […]...
- Теореми § 2. Трикутники 11. Теореми 269. Теорема Умова Висновок 4.1 Кути АОС і СОВ – суміжні ∠AOC + ∠COB = 180° 8.2 X належить серединному перпендикуляру відрізка AB ХА = ХВ 9.1 ?ABC – рівнобедрений з основою АС 1) ∠A = ∠C; 2) бісектриса кута В є медіаною і висотою 10.3 Два кути трикутника ABC […]...
- Означення. Аксіоми Геометрія Основні властивості найпростіших геометричних фігур Означення. Аксіоми Геометрія – це наука про властивості геометричних фігур. Зверніть увагу: геометрична фігура – це не тільки трикутник, коло, піраміда тощо, а й будь-яка множина точок. Планіметрія – це розділ геометрії, у якому вивчаються фігури на площині. Точка і Пряма є основними поняттями планіметрії. Це означає, що цим […]...