Дії над радикалами
УРОК 36
Тема. Дії над радикалами
Мета урокую Познайомити учнів з діями над радикалами: додавання і віднімання, множення і ділення; піднесення радикала до степеня; добування коренів з радикалів; зведення до раціонального вигляду членів дробових ірраціональних виразів.
І. Перевірка домашнього завдання
1. Три учні відтворюються розв’язування вправ № 22, 26 і 38 на дошці.
2. У цей час клас порівнює (усно) вирази, подані в таблиці 15.
1 | 2 | 3 | 4 | |
1 |
|
| 2 | 2 |
2 |
|
|
|
|
3 |
|
|
|
|
4 |
| 1 * |
|
|
3. Відповіді на запитання учнів, що виникли в процесі виконання домашнього завдання.
II. Сприймання і усвідомлення нового матеріалу
1. Додавання і віднімання радикалів виконується так само, як і додавання і віднімання раціональних одночленів (многочленів).
Приклади:
3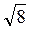 – 5
– 5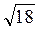 + 12
+ 12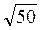 = 3-2
= 3-2 – 5-3
– 5-3 + 12-5
+ 12-5 = 6
= 6 – 15
– 15 + 60
+ 60 = 51
= 51 ;
;
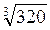 – (2
– (2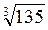 – 3
– 3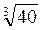 ) = 4
) = 4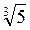 – 2-3
– 2-3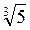 + 3-2
+ 3-2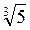 = 4
= 4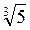 – 6
– 6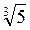 + 6
+ 6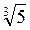 = 4
= 4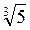 .
.
2. При множенні (діленні) радикалів з різними показниками спочатку їх треба привести до одного показника, а потім перемножити (поділити) підкореневі вирази і записати добуток (частку) під знак кореня з тим самим показником.
Приклади:
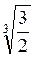 –
– 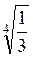 =
= 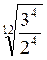 –
– 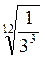 =
= 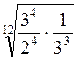 =
= 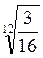 ;
; 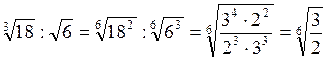 .
.
Виконання вправ № 54 (1, 2), 55 (1, 2)
3. При піднесенні радикала до степеня, можна піднести до цього степеня підкореневий вираз, залишивши той самий показник кореня.
Наприклад: 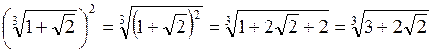 .
.
4. Щоб добути корінь із радикала, можна із підкореневого виразу добути корінь з показником, що дорівнює добутку двох даних показників.
Наприклад: 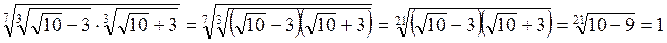 .
.
5. У деяких задачах корисно звільнятися від ірраціональних виразів у знаменнику дробу.
Звільнитися від ірраціональності в знаменнику дробу – це означає перетворити дріб, знаменник якого містить корені, до нового дробу, тотожно рівному даному, знаменник якого коренів не містить.
Якщо знаменник дробу являє собою радикал чи добуток радикала на раціональний множник, то слід чисельник і знаменник дробу домножити на таку степінь кореня того самого показника, щоб отримати степінь з показником, що дорівнює показнику кореня.
Наприклад: 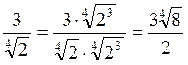 ;
; 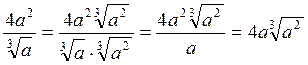 .
.
Якщо знаменник дробу є сума (або різниця) квадратних радикалів, то дріб можна привести до раціонального вигляду, помноживши чисельник і знаменник на різницю (або на суму) тих самих радикалів.
Наприклад: 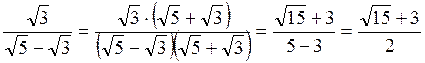 ;
; 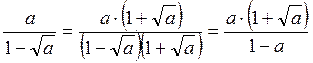 , якщо a
, якщо a  0, a? 1.
0, a? 1.
Якщо знаменник дробу є сума (різниця) кубічних радикалів, то, щоб позбутися ірраціональності в знаменнику, слід домножити чисельник і знаменник дробу на неповний квадрат різниці (суми) тих самих радикалів.
Наприклад: 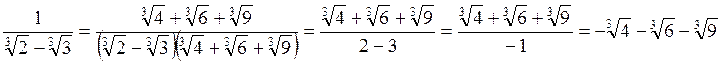 .
.
Виконання вправ № 57 (2, 6), 58 (4, 5).
III. Підведення підсумків уроку
IV. Домашнє завдання
Розділ III § 1 (5). Запитання і завдання для повторення розділу III № 38-46. Вправи № 19 (5), 40, 57 (1, 5), 58 (1).
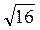
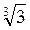
 * 3
* 3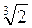
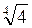
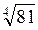
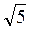 *
* 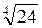
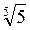
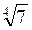 *
* 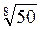
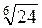 *
* 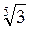
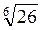
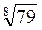
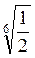
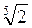 * 1
* 1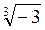 *
*