Дії над векторами
192.
А)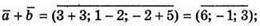 
Б)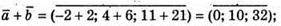 
В)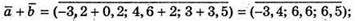 
Г)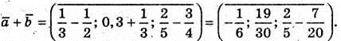 
193.
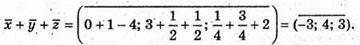
194.
А)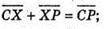 
Б)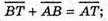 
В)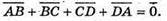 
195.
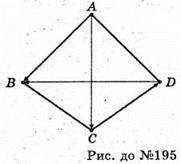
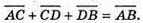
196.
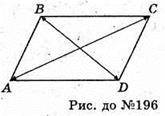
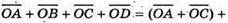
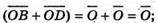
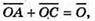бо 
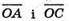– протилежні вектори,
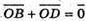(аналогічно).
197.
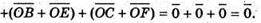
198.
А)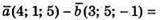 
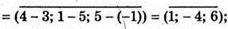
Б)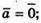 
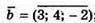
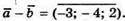
199.
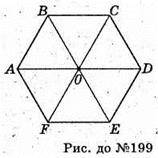
А)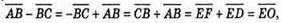 
Але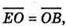 
оскільки 
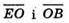– однаково напрямлені і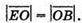 
Отже,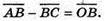 
Б)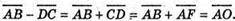 
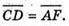
200.
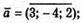
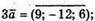
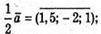
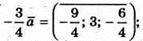
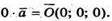
201.
А)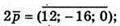 
Б)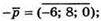 
В) 
Г)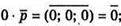 
Г)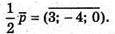 
202.
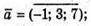
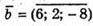
А)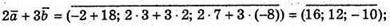 
Б)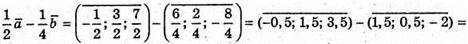 
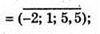
В)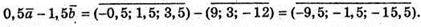 
203.
А)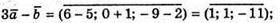 
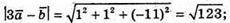
Б)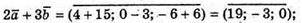 
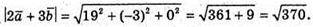
204.
А)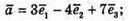 
Б)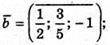 
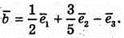
205.
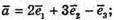
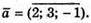
206.
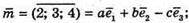
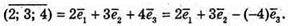
Отже, а = 2, b = З, с = -4.
207.
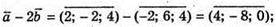
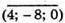
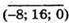– колінеарні, оскільки -8 = 4 × (-2);
16 = -8 × (-2); 0 = 0 × (-2).
208.
А)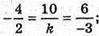 
звідси 
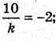k = -5;
Б)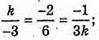 
звідси k= 1.
209.
А)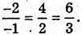 
Отже, 
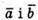– колінеарні;
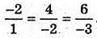Отже, 
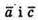колінеарні.
Звідси: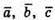 
– компланарні.
Б)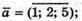 
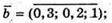
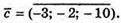
Якщо вектори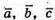 
– компланарні, то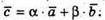 
Тоді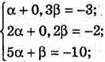 
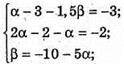
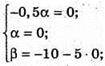
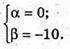
Отже,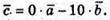 
Звідси: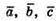 
– компланарні.
210.
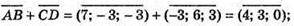
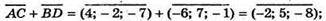
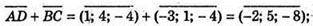
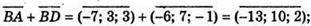
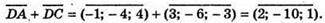
211.
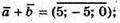
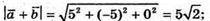
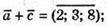
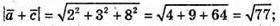
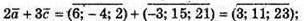
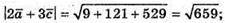
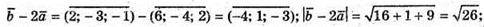
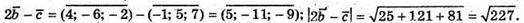
212.
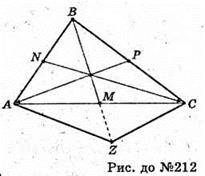
Знайдемо суму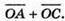 
Добудуємо паралелограм ка сторонах ОА і ОС.
AOCZ – паралелограм, М – середина АС (за умовою), MZ = ОМ (за побудовою).
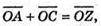оскільки 
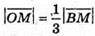(властивість точки перетину медіан).
Тоді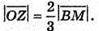
За тією самою властивістю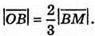 
Звідси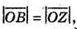 
але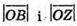 
– протилежно напрямлені.
Тому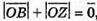 
оскільки 
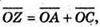то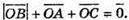 
213.
А)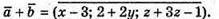 
Оскільки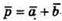 
і 
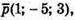то:
Х – 3 = 1; x = 4; 2 + 2у = -5; 2у = -7; у = -5,3; z + 3z – 1 = 3; 4z = 4; z = 1.
Отже, х = 4; у = -3,5; z = 1.
Б) x – 3 = 3; x = 6; 2 + 2у = -7; у = -4,5; 4z – 1 = 12;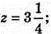 
В) х – 3 = 1; х = 2; 2 + 2у = 6; 2у = 4; y = 2; 4z – 1 = -9; z = -2.
214.
Якщ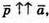о 
то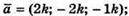 
k > 0.
Тоді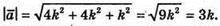 
За умовою 
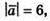тому 3k = 6; k = 2.
Отже,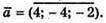 
215.
Якщо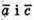 
– протилежно напрямлені і 
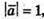то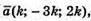 
де k < 0
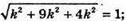
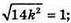
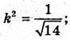
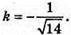
Звідси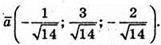 
216.
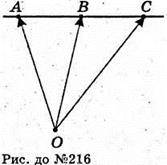
Якщо точки А, В, С лежать на одній прямій, то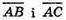 
– колінеарні.
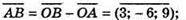
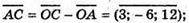
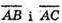– неколінеарні, бо 
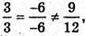тому A, B, С не лежать на одній прямій.
217.
Нехай Р(х; у; z). Тоді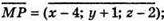 
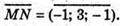
Якщо Р? MN, то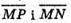 
– колінеарні, тоді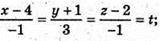 
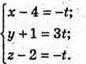
Оскільки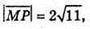 
то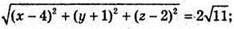 
(-t)2 + (3t)2 + (t)2 = 4 × 11; 11t2 = 44; t2 = 4; t = 2 або t = -2.
Тоді: х – 4 = -2 або x – 4 = 2; x = 2 або х = 6;
У + 1 = 3 × 2 або y + 1 = -3 × 2; у = 5 або y = -7;
Z – 2 = -2 або z – 2 = 2; z = 0 або z = 4.
Отже, Р(2; 5; 0) або Р(6; -7; 4)
218.
А)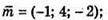 
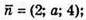
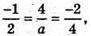звідси 
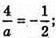а = -8.
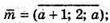
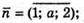
Б)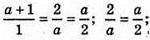 
а2 = 4; а = 2 або о = -2.
Але a = 2 не задовольняють умові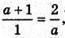 
Тому а = 2 не є розв’язком.
Дана умова виконується при а = -2. Отже, а = -2.
В) m = (3; 5 – а; а); n = (5 + а; 7а+ 1; 2);
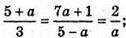
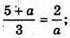
А2 + 5а – 6 = 0; а = 1 або а = -6, але а = -6 не задовольняє умові
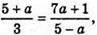тому а = -6 не є розв’язком. Отже, а = 1.
219.
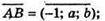
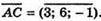
Якщо А, В, С лежать на одній прямій, то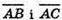 
– колінеарні,
Тоді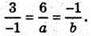 
Звідси 3а = -6; а = -2; 36 = 1;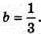 
220.
Якщо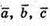 
– компланарні, то знайдуться такі числа α і β, що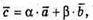 
Або:
А)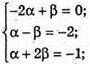 
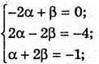
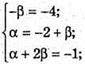
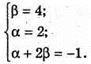
Але α = 2, β = 4 не задовольняє умові α + 2β = -1.
Отже, таких чисел α і β не існує.
Тому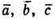 
– не компланарні.
Б)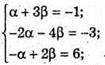 
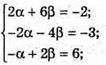
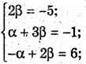
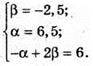
Але α = 6,5: β = -2,5 не задовольняють умові -α + 2β = 6.
Отже, система розв’язків не має. Не існує таких α і β, що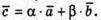 
Тому,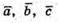 
– некомпланарні.
221.
Якщо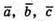 
– компланарні, то 
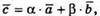Або
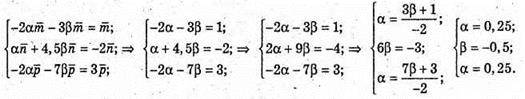
Отже,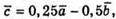 
тому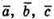 
– компланарні.
222.
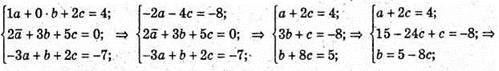
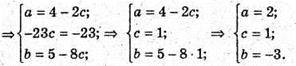
Отже, а = 2; b = -3; с = 1.
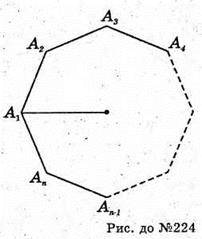
224.
Якщо A 1A 2A3A1 – правильний, то OA1 = ОА2 = ОА3 – … – ОАn.
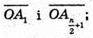
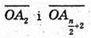– протилежні, тому
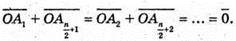
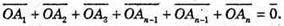
Отже,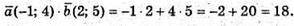 
225.
(1 votes, average: 5.00 out of 5)
Loading...