Головна ⇒ 📌Математика ⇒ ГЕОМЕТРИЧНІ ПОБУДОВИ

ГЕОМЕТРИЧНІ ПОБУДОВИ

РОЗДІЛ 4 КОЛО І КРУГ. ГЕОМЕТРИЧНІ ПОБУДОВИ

& 18. ГЕОМЕТРИЧНІ ПОБУДОВИ

Користуючись лінійкою1 і циркулем, можна виконувати багато геометричних побудову тобто креслити геометричні фігури. Розглянемо спочатку, як виконувати найпростіші геометричні побудови.

ЗАДАЧА 1

Побудуйте трикутник із даними сторонами.

РОЗВ’ЯЗАННЯ. Нехай дано три відрізки: а, b і с (мал. 224). Треба побудувати трикутник, сторони якого дорівнювали б цим відрізкам. За допомогою лінійки проводимо довільну пряму, позначаємо на ній довільну точку В і відкладаємо

циркулем на цій самій прямій відрізок ВС = а. Розхилом циркуля, що дорівнює с, описуємо дугу кола з центром В. З того самого боку від прямої СВ описуємо дугу

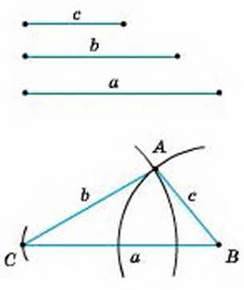
Мал. 224

1 Вважаємо, що лінійка без поділок.

Кола радіуса b з центром С. Точку перетину А цих дуг сполучаємо відрізками з точками С і В. Трикутник ABC – той, який треба було побудувати, бо його сторони ВС, АС і АВ дорівнюють даним відрізкам.

Зверніть увагу! Якщо побудовані дуги не перетинаються, трикутник побудувати не можна. Це буває тоді, коли один із даних відрізків більший за суму двох інших або дорівнює цій сумі.

ЗАДАЧА

Побудуйте кут, що дорівнює даному куту.

РОЗВ’ЯЗАННЯ. Нехай дано кут АОВ і потрібно побудувати кут КРТ, що дорівнює куту АОВ (мал. 226). Будуємо промінь РТ і дуги рівних радіусів із центрами О і Р. Нехай одна з цих дуг перетинає сторони кута АОВ в точках А і В, а друга – промінь РТ в точці Т. Далі розхилом циркуля, що дорівнює АВ, описуємо третю дугу з центром Т. Якщо вона перетинає другу дугу в точці К, проводимо промінь РК. Кут КРТ – той, який вимагалось побудувати. Адже трикутники КРТ і АОВ рівні (за трьома сторонами), тому ∠KPT = ∠АОВ.

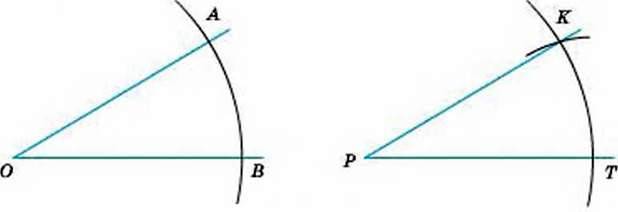
Мал. 225

ЗАДАЧА 3

Побудуйте бісектрису даного кута.

РОЗВ’ЯЗАННЯ. Нехай АОВ (мал. 226) – даний кут. Довільним розхилом циркуля опишемо дугу з центром О. Hехай А і В – точки перетину цієї дуги з променями ОА і ОВ. Із центрів А і В опишемо дуги такими самими радіусами. Якщо D – точка перетину цих дуг, то промінь OD – бісектриса кута АОВ. Справді, ∆AOD = ∆BOD за трьома сторонами. Тому ∠AOD = ∠DOB.

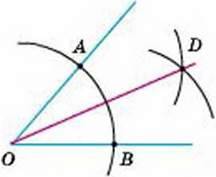
Мал. 226

ЗАДАЧА 4

Поділіть даний відрійок навпіл.

РОЗВ’ЯЗАННЯ. Нехай АВ – даний відрізок (мал. 227). З точок А і В радіусом АВ описуємо дуги. Вони перетнуться в деяких точках С і D.

Пряма CD точкою М ділить даний відрізок навпіл.

Справді, ∆ACD = ∆BCD за трьома сторонами, тому ∠ACM = ∠ВCM. За першою ознакою рівності трикутників ∆ACM = ∆ВСМ. Отже, AM = ВМ.

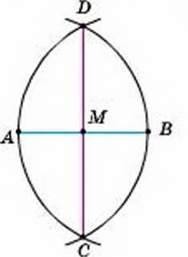
Мал. 227

ЗАДАЧА 5

Через дану точку Р проведіть пряму, перпендикулярну до даної прямої а.

РОЗВ’ЯЗАННЯ. Залежно від того, лежить чи не лежить точка Р на прямій а, задачу можна розв’язувати, як показано на малюнках 228 і 229. Опишіть і обгрунтуйте ці побудови самостійно.

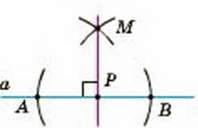
Мал. 228

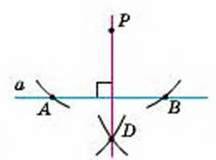
Мал. 229

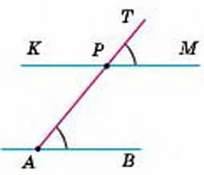
Мал. 230

ЗАДАЧА 6

Через точку Р, що не лежить на прямій АВ, проведіть пряму, паралельну прямій АВ.

РОЗВ’ЯЗАННЯ. Через точку Р і довільну точку А прямої АВ проводимо пряму АТ (мал. 230). Будуємо кут ТРМ, що дорівнює куту РАВ, так, щоб ці кути стали відповідними при прямих РМ, АВ і січній АР. Побудована таким способом пряма РМ задовольняє задачу, бо вона проходить через дану точку Р і паралельна прямій АВ, оскільки ∠TPM = ∠РАВ.

Для допитливих

Геометричними побудовами часто доводиться займатися багатьом людям. Ще в доісторичні часи майстри, які робили колеса до колісниць, уміли ділити коло на кілька рівних частин. Тепер виконувати такі побудови доводиться фахівцям, які проектують чи виготовляють шестерні, дискові пилки (мал. 231), турбіни та різні роторні механізми.

Як би ви поділили коло, наприклад, на 5, 6 чи 7 рівних частин?

Основні креслярські інструменти – лінійка і циркуль – майстровим людям були відомі ще кілька тисячоліть тому. Слово лінійка походить від слова “лінія”, яке латинською мовою спочатку означало “льняна нитка”. І слово циркуль – латинського походження. Спочатку слово “циркулює” означало коло, круг, обвід.

У Стародавній Греції лінійку і циркуль визнавали єдиними приладами геометричних побудов. Задачу на побудову вважали розв’язаною, якщо в ній всі побудови виконувалися тільки за допомогою лінійки і циркуля. Тепер фахівці, виконуючи ті чи інші побудови, використовують косинець, транспортир, рейсмус, рейсшину та інші креслярські засоби.

Мал. 231

Запитання і завдання для самоконтролю

1. Поясніть, як побудувати трикутник за трьома даними сторонами.

2. Як побудувати кут, що дорівнює даному?

3. Як побудувати бісектрису даного кута?

4. Як поділити даний відрізок навпіл?

5. Як через дану точку провести пряму, перпендикулярну до даної прямої?

6. Як через дану точку провести пряму, паралельну даній прямій?

Виконаємо разом

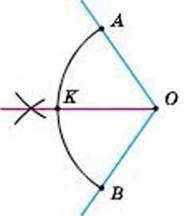
1. Поділіть дану дугу кола на дві рівні частини. Нехай дано дугу АВ кола з центром О

(мал. 232). Уявімо кут АОВ і проведемо його бісектрису ОК. Трикутники АОК і ВОК рівні, тому й дуги АК і ВК дорівнюють одна одній.

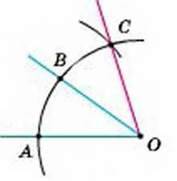
2. Побудуйте кут, більший від даного удвічі. Нехай АОВ – даний кут (мал. 233). Опишемо дугу кола із центром О. Нехай вона перетне сторони даного кута в точках А і В. З точки В, як із центра, зробимо засічку ВС = ВА і проведемо промінь ОС. Кут АОС вдвічі більший за ∠AOВ, бо ∠AOB = ∠ВОС.

Мал. 232

Мал. 233

ЗАДАЧІ І ВПРАВИ

Виконайте усно

526. Чи правильне твердження: “Щоб поділити кут на дві рівні частини, треби провести його бісектрису”?

527. Поділіть даний кут на 4 рівні частики.

528. Побудуйте прямий кут.

529. Побудуйте кут, міра якого: а) 45°; б) 22,5°; в) 60°; г) 30°.

530. Побудуйте кут, утричі більший за даний гострий кут.

531. Поділіть даний відрізок на 4 рівні частини.

532. Як поділити навпіл відрізок, довжина якого н кілька разів більша за найбільший розхил циркуля?

533. Побудуйте відрізок, який у два рази більший за даний.

534. Побудуйте відрізок, у 3 рази більший за даний відрізок.

535. Поділіть дану дугу кола на чотири рівні частини.

536. Побудуйте трикутник, рівний даному трикутнику.

537. Побудуйте рівносторонній трикутник за даною його стороною.

538. Побудуйте рівнобедрений трикутник за основою і бічною стороною.

539. Побудуйте прямокутний трикутник за двома катетами.

540. Побудуйте трикутник за двома сторонами і кутом між ними.

541. Побудуйте рівнобедрений трикутник за бічною стороною і кутом при вершині.

542. Побудуйте трикутник за стороною і прилеглими кутами.

54З. Побудуйте рівнобедрений трикутник за основою і кутом при основі.

544. Побудуйте трикутник за сторонами 3 см, 4 см і 5 см.

545. Побудуйте трикутник і проведіть його медіани.

546. Дано трикутник. Побудуйте його бісектриси.

547. Дано трикутник. Побудуйте його висоти. Розгляньте всі можливі випадки.

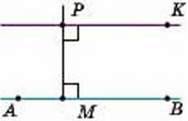
548. Щоб через дану точку Р провести пряму, паралельну АВ, можна спочатку провести PM ⏊ АВ, а потім РК ⏊ РМ (мал. 234). Обгрунтуйте цю побудову.

549. Через дану точку проведіть пряму, яка перетинає дану пряму під даним кутом.

Мал. 234

550. Історична задача (Стародавня Греція, V cм. до н. е.). За допомогою циркуля та лінійки поділити даний довільний кут на три рівні частини.

Архімед розв’язував цю задачу за допомогою “вставки”.

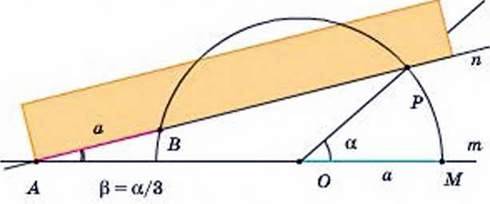
Нехай а – даний кут. Опишемо з вершини кута коло з радіусом а, де а – відстань між відмітками на лінійці (мал. 235, а). Через точку Р проведемо пряму так, щоб довжина відрізка між точками В і А дорівнювала а. Отримаємо ∠ОАВ = В.

Доведіть, використовуючи малюнок 235, б, що за цих умов а = 3β.

Мал. 235, а

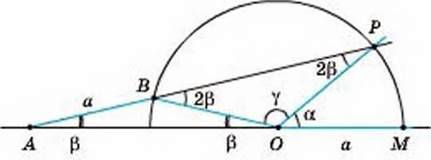
Мал. 235, б

Практичне завдання

551. Побудуйте квадрат. Поділіть його кут на три рівні частини двома способами: а) методом Архімеда за допомогою вставки; б) за допомогою циркуля та лінійки без поділок.

ВПРАВИ ДЛЯ ПОВТОРЕННЯ

552. Доведіть, що кожна сторона квадрата ABCD з прямою АС утворює кути по 45°.

553. Визначте вид трикутника, у якому сума двох кутів менша від третього.

554. Під яким кутом перетинаються дві медіани рівностороннього трикутника?