Геометричні тіла і поверхні
219.
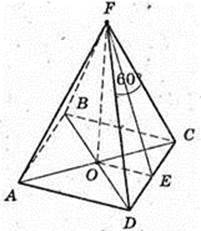
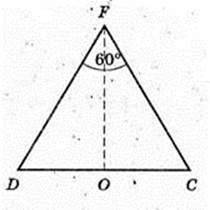
Дано: FABCD – піраміда правильна, AB = 6 см, ∠DFC = 60°.
1)
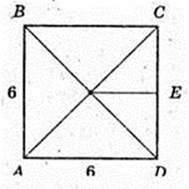
Знайти SABCD i висоту FO. SABCD = 62 = 36 (см2). ΔDFC, DF = FC за умовою
І ∠DFC = 60° → DF = FC = DC = 6 (см). 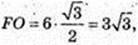
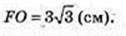
Відповідь: 36 см2, 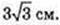
2)
∠FCA – ? 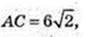
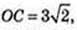
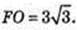
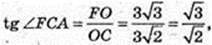
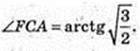
Відповідь: 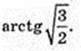
3)
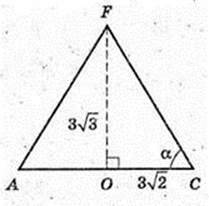
∠AFC – ? 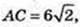
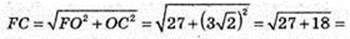
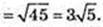
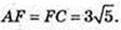
AC2 =AF2 + FC2 – 2AF × FC × cos∠AFC,
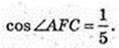
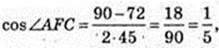
Відповідь: 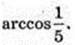
4)
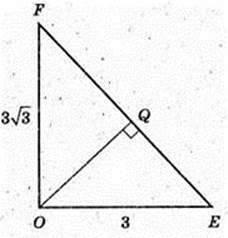
OQ – ? ΔOFE, OE + CD, OE = 3cм, 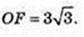
∠ FOE = 90°, OQ + FE.
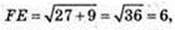 FE = 6.
FE = 6.
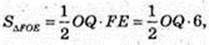
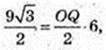
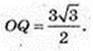
Відповідь: 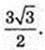
220.
Дано: ABCDT – піраміда правильна, ТЕ – апофема, TE = l.
Двогранний
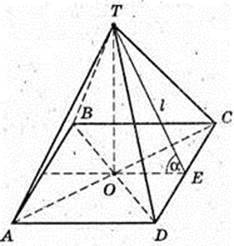
1)
SABCD – ? ТО – ?
ТО – висота піраміди. OE + DC, DE = EC.
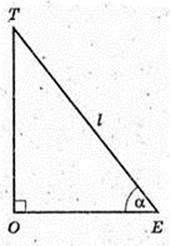
TE + DC, ∠TEO = α,ТЕ = І.
ΔTEO: ∠O = 90°, ∠E = α, TЕ = Z → ТО = I sin α,
ТО = H = I sin α, OE = I cos α, AD = 2OE = 2l cos α,
SABCD = AD2 = 4l2 cos2 α.
Відповідь: 4l2 cos2 а; l sin α.
2)
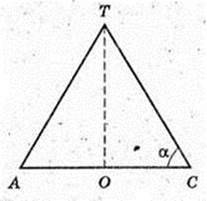
∠TCA – ?
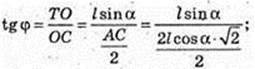
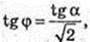
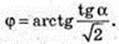
Відповідь: 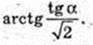
3)
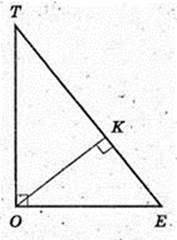
∠ATC -? ΔATC: ∠ATC = 180°- 2α,
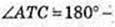
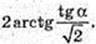
Відповідь: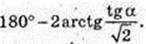
4) ΔTOF. OK + TE, OK -?
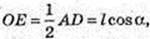
TO = l sin α → TE = l.
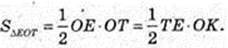
I cos α × I sin α = I × OK,
OK = I sin α cos α. 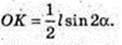
Відповідь:
221.
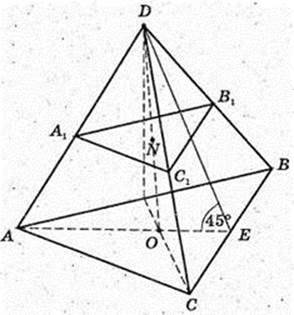
Дано: DABC – піраміда правильна.
Бічна грань нахилена до площини основи під кутом 45°,
AB = BC =AC = a. DO = Н.
1)
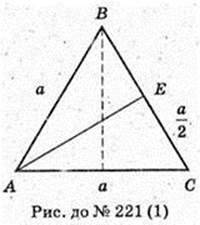
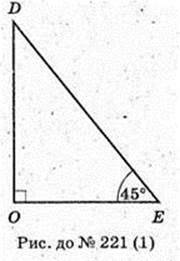
DO – ? DE + BC, AE + BC, ∠DEA=45°.
ААВС: AB = BC =AC = a, ∠LA = ∠B = ∠C = 60°. AE + ВС,
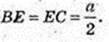
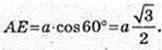
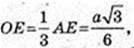
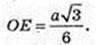
ΔDOE: ∠O = 90°,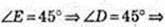
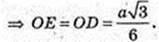
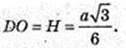
Відповідь: 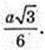
2)
∠DBO – ?φ -?
ΔDOB: ∠O = 90°, 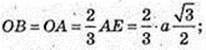
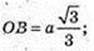
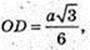
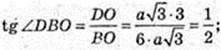
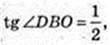
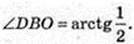
Відповідь: 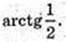
3)
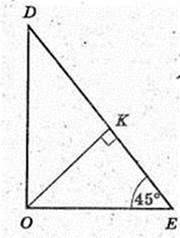
ΔDOE, ∠DOE = 90°. OK + DE, OK – ?
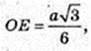
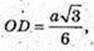
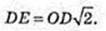
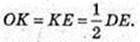
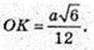
Відповідь: 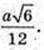
4) Переріз піраміди – ΔA1B1C1 A1B1C1¦ABC,
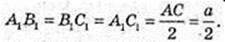
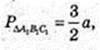
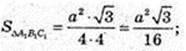
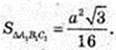
Відповідь·.
222.
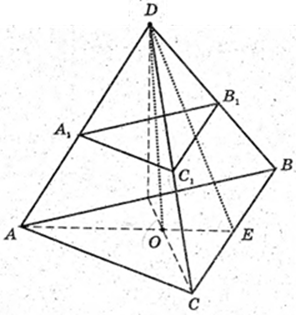
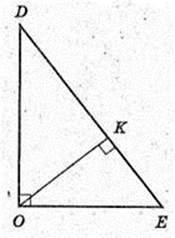
Дано: DABCD – піраміда правильна. AB = BC = AC = а.
Апофема DE = р, DO = H – висота.
1)
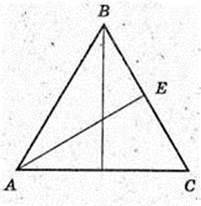
Знайти DO.
ΔABC: AB = BC =AC = а. O – центр трикутника.
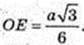 DO = H – висота, ∠DOE = 90°, DE = р,
DO = H – висота, ∠DOE = 90°, DE = р,
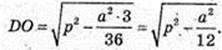
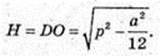
Відповідь: 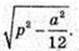
2)
∠DEA – ? ∠DEA = ∠DEO – ?
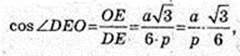
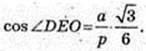
Відповідь: 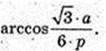
3) ∠DBO -?
ΔDBO: ZO = 90°,
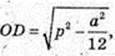
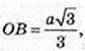
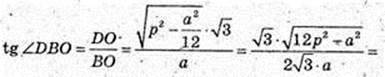
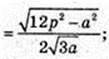
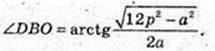
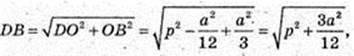
Або: 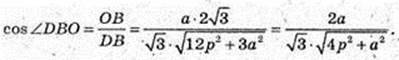
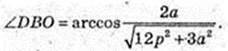
Відповідь: 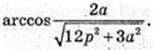
4) OK + DE, OK – ?
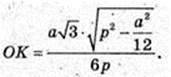
Відповідь: 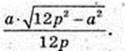
5) 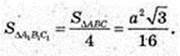
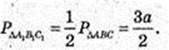
Відповідь: 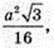
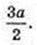
223.
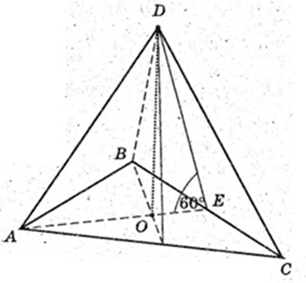
Дано: ABCD – піраміда, правильна.
Висота DO = H. 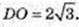
Бічна грань утворює із площиною ABC кут 60°. AB – ?
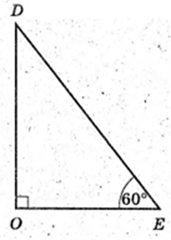
ΔDOE: AE + ВС, DE + ВС, ∠DEA = 60°.
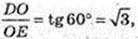
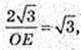 OE = 2.
OE = 2.
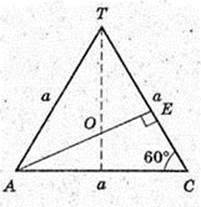
ΔАВС: AB = BC = AC, OE = 2 → AE = 6,
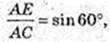
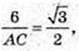
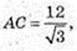
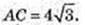
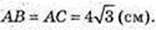
Відповідь: 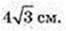
224.
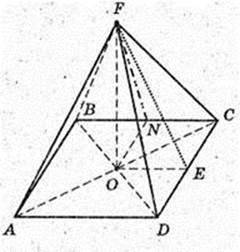
Дано: ABCDF – піраміда, ABCD – прямокутник.
AB = 3 см, AD = 4 см, FO = Н, FO = 6 см.
1) ∠FCA – ? ABCD – прямокутник, AB = 3 см, AD = 4 см → BD = 5 см,
AC = BD = 5 см, OC = 2,5 см.
ΔFOC: ∠O = 90°, OF = 6 см.
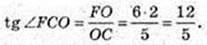
FCO = arctg 2,4.
Відповідь: arctg 2,4.
2) FC – ?
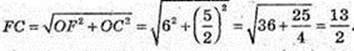
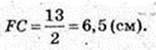
Відповідь: 6,5 cм.
3) FE – ? FN – ? ΔFEC:

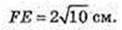
ΔFNO: ON + BC, ∠FON = 90°,
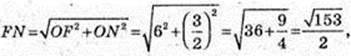
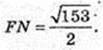
Відповідь: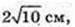
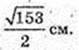
4) ∠FEO – ? ∠FNO – ?
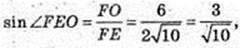
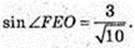
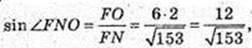
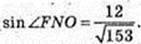
Відповідь: 
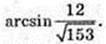
5) 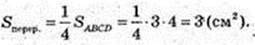
Sперер. = З cм2.
Відповідь: 3 cм2.
225.
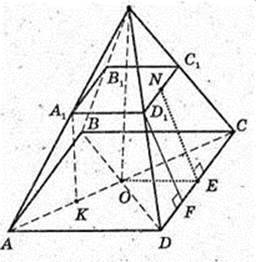
ABCDA1B1C1D1 – правильна зрізана піраміда.
A1K – висота, A1K = H = 7 cм, AB = BC = DC = AD= 10 cм,
A1B1 = B1C1 = D1C1 =A1D1 = 2 см.
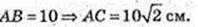
1)
C1C – ? 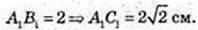
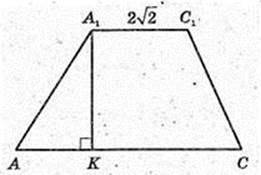
AA1C1C – трапеція, рівнобічна.
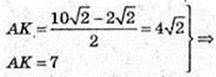
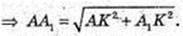
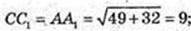
CC1 = AA1 = BB1 = DD1=9 cм. D1F – ? D1F + DC.
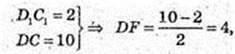 DF = 4.
DF = 4.
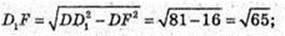
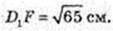
Відповідь: 9 cм, 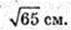
2)
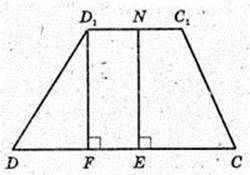
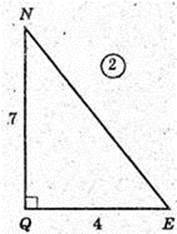
Трапеція DD1C1C, D1N = NC1. DE = EC. ∠NEO -?
NQ = A1K = 7. 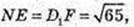 QF = 4.
QF = 4. 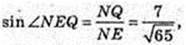
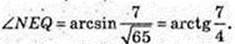
Або: 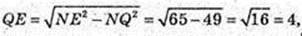 QE = 4,
QE = 4,
Тоді 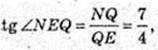
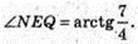
∠A1AK – ? 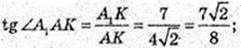
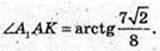
Відповідь: 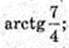
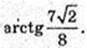
3)
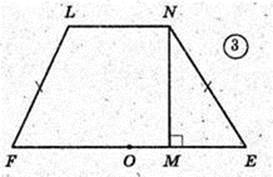
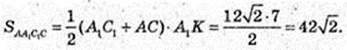
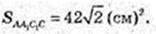
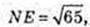
FLNE – трапеція. LN = 2, FE = 10.
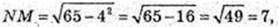
NM = 7, NM = A1K = Hпіраміди
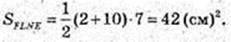
Відповідь: 42 см2, 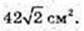
4) Переріз KD1C1N, D1K ¦ A 1A; C1N ¦ A1A.
AA1 = 6 см, D1K = 9 см, C1N = 9 см, KN = 10 см, D1C1 = 2, C1Q + KN.
KD1C1N – рівнобічна трапеція.
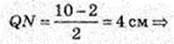
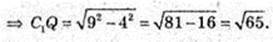
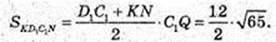
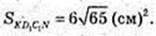
Відповідь: 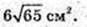
226.
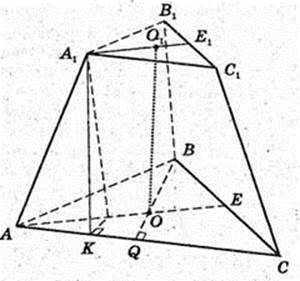
Дано: ABCA1B1C1 — правильна зрізана трикутна піраміда,
Висота A1F, A1F = 7 см. AB = BС = AC = 10 см, A1B1 = B1C1 = A1C1 = 2 см.
1) Знайти AA1. А1K + AC, A1K – ?
ΔАВС – правильний, ΔΑ1В1C1 – правильний.
AB = BC = AC = 10 см, AE + BC,
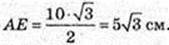
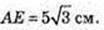
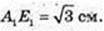
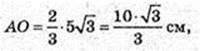
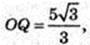 BQ + АС. τ. O – центр ΔABC, τ. O1 – центр ΔA1B1C1
BQ + АС. τ. O – центр ΔABC, τ. O1 – центр ΔA1B1C1
OO 1 + (ABC), OO1 + (A1B1C1).
За умовою A1F – висота піраміди, A1F + (ABC). A 1F = 7 cм, FO = A1O1
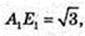
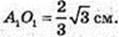
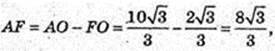
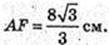
ΔAA1F: ∠A1FA = 90°, A 1F = 7,
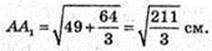
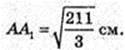
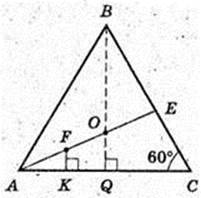
ΔABC: 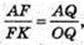 FK – ?
FK – ?
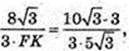
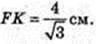
ΔA1FK: ∠A1FK = 90°, 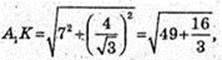
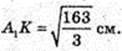
Відповідь: 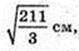
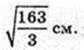
2)
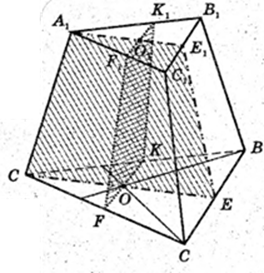
А 1K + АС, ∠A 1KF – ? 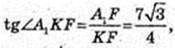
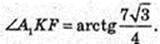 ∠A1AF – ?
∠A1AF – ?
ΔA1FA: ∠A1EA = 90°, A1F = 7,
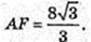
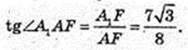
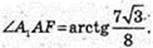
Відповідь: 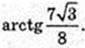
3)
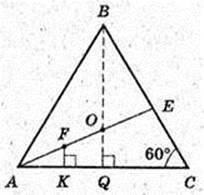
Переріз KOFF1O1K має найменшу площу.
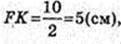
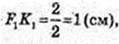 OO1 = 7 см.
OO1 = 7 см.
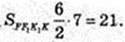 Sнайм. = 21см.
Sнайм. = 21см.
Переріз AA1E1E має найбільшу площу серед інших перерізів,
Які проходять через точки O і O1.
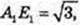
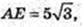 OO1 = 7.
OO1 = 7.
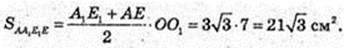
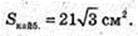
Відповідь: 21 см2, 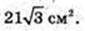
227.
1) Якщо усі бічні ребра піраміди рівні між собою, то їх ортогональні проекції на площину основи піраміди теж рівні між собою, тоді проекція вершини піраміди рівновіддалена від усіх вершин основи піраміди, тобто проекція вершини піраміди є центр кола, описаного навколо основи піраміди.
2) Якщо усі бічні ребра піраміди нахилені до площини основи піраміди під однаковими кутами, то ортогональні проекції усіх бічних ребер однакові і тоді центр кола, описаного навколо основи піраміди є ортогональною проекцією вершини піраміди.
228.
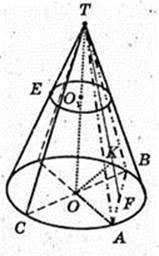
Прямий круговий конус, H = ТО = 4 cм, Rосн. = OA = OB = 3.
1) AT – ? ΔААОТ: ∠AOT = 90°, ОТ = 4 см,
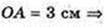
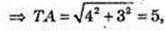 l =AT = 5 см.
l =AT = 5 см.
Відповідь: 5 см.
2) SΔTBC – ? Δ ТВС: ТО = 4, CB = 6.
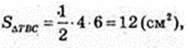 S = 12 см2.
S = 12 см2.
Відповідь: 12 см2.
3) ∠ CTB – ? 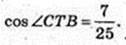
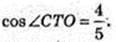
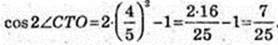
Відповідь: 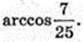
4)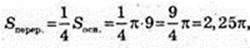
S перер. = 2,25 πсм2.
Відповідь: 2,25π см2.
5)
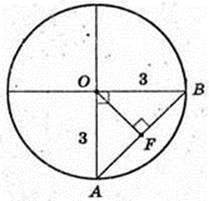
S ΔTBC – ? ∠ AOB = 90°, OA = OB = R,
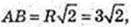
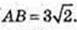 AF = FB, TF1AB,
AF = FB, TF1AB,
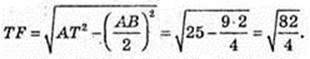
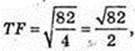
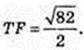
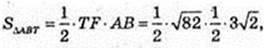
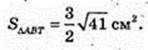
Відповідь: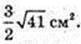
6)
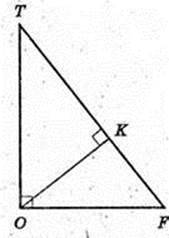
OK + (ATВ), OK – ?
ΔTOF: ∠TOF = 90°, ТО = 4,
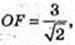
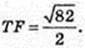
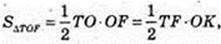 ОК = х,
ОК = х,
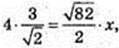
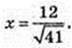
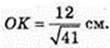
Відповідь: 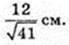
229 .
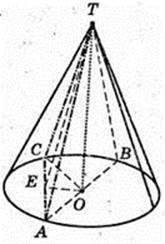
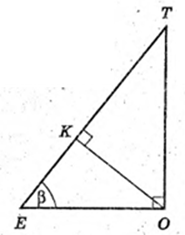
Дано: прямий круговий конус. ТА – твірна, ТА = 4 см.
∠ АТВ = 60°, де ТО = H.
Площина ACT утворює кут β з площиною основи.
1)
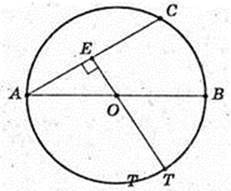
S ΔATC -?
ΔАTО: ∠ AOT = 90°, AB = 4 см,
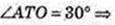
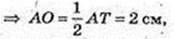
AO = R = 2 см, R = 2 см.
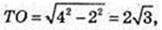
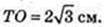
ОE + AC → AE = CE, ТО + (ABC), ТЕ – похила → TE + AC, ∠ TEO = β.
ΔTOE: ∠ TOE = 90°, ∠ TEO = β,
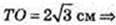
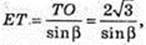
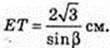
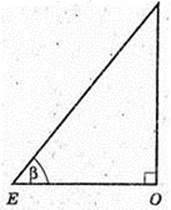
ΔОАЕ: 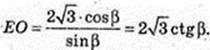
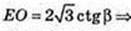
ZOEA=90°, AO=R=2,
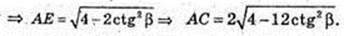
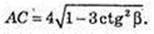
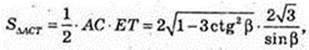
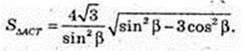
Відповідь: 
2)
OK + (TАС), OK – ?
Δ ΕΤΟ: ∠ EOT= 90°, ∠ TEO = β,
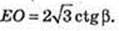
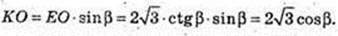
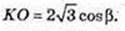
Відповідь: 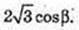
3)
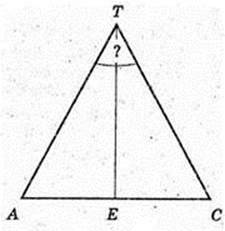
∠ATC – ?
ΔАТС: TA = TC, 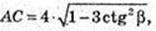
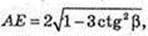 AE = EC, ТЕ + АС.
AE = EC, ТЕ + АС.
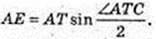 AT = 4,
AT = 4,
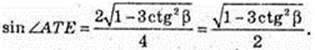
Cos 2α = 1 – 2 sin2 α.
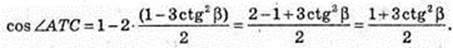
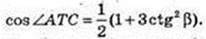
Відповідь: 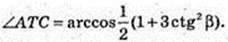
4)
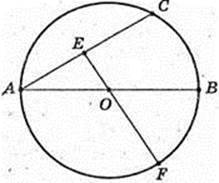
FE – ?
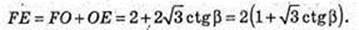
Відповідь: 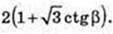
5)
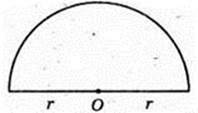
OE < OF, OE < R,
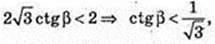
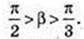
Відповідь: 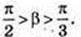
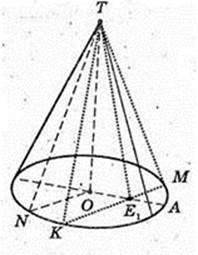
230.
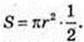
1) Sб. к.= πRl, l = r,
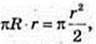
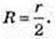
Відповідь: 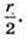
2) l = r, Відповідь: г.
3) ТО – ? AT = I = г.
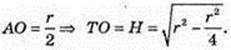
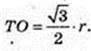
Відповідь: 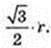
4) ∠ATB – ? ∠ATO – ?
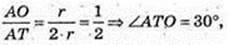
∠ATB = 60°. Відповідь: 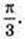
5) 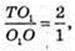
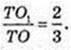
L перер. -?
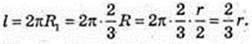
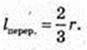
Відповідь: 
232.
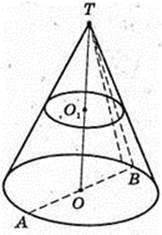
TABC – піраміда, в ΔАВС ∠ACB = 90°, AB = 4 см,
CA = CB = 2.
Кут між гранями ABT і ABC дорівнює 60°.
TC + (ABC), TC = H i AC = BC → TA = TB.
1)
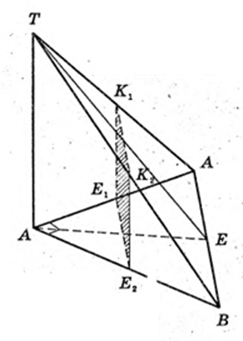
TC – ? CE +AB, AE = BE = 2 → CE = 2.
TE + AB. ∠TEC = 60°.
ΔТЕС: ∠C = 90°, ∠B = 60°,
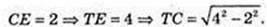
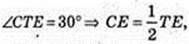
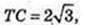
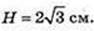
Відповідь: 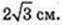
2)
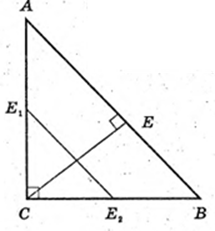
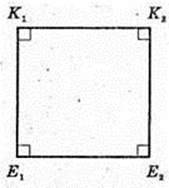
ΔABC, ∠C = 90°. AE1 = E1C, BE2 = E2C.
Переріз K1K2E1E1, K1E1 ¦ TC, K2E2 ¦TC.
E1E2 = AB : 2 = 2, E1E2 = 2.
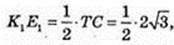
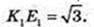
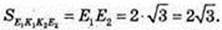
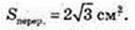
Відповідь: 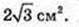
3)
Конус, ТО = TC = Hk.
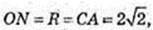
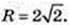
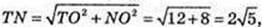
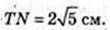
Відповідь: 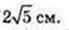
4)
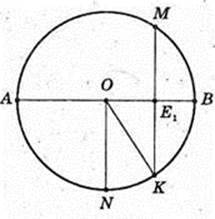
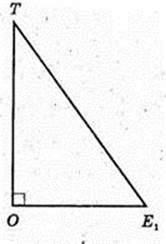
∠NOA = 90°; OE1 = E1A, KE1 ¦ NO. SΔKTM – ?
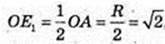
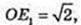
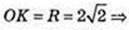
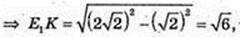
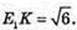
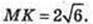
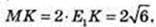
ΔTOE1: ∠O = 90°, 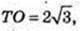
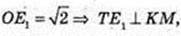
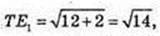
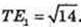
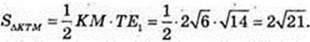
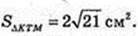
Відповідь: 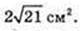
233.
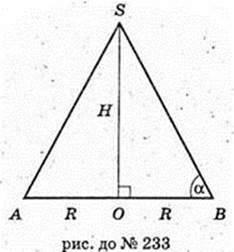
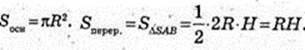
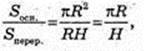
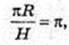
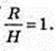
R = H, 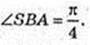
Відповідь: 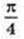 або 45°.
або 45°.
234 .
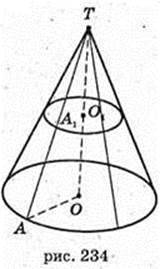
Конус прямий круговий, висота Н.
TO = H. TO1 – ?
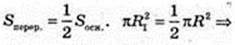
2 R = R2 →
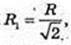
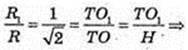
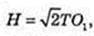
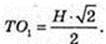
Відповідь: 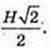
235.
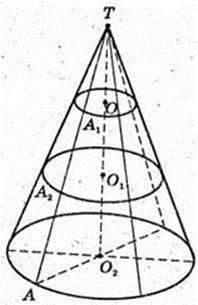
Конус, висота TO2 = Н.
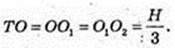
S пер +S1пер =πr2 + π(2r)2 = π × 5r2;
Sосн. = πR2 = π(3r)2 = 9πr2.
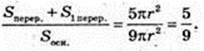
Відповідь: 
237.
Перерізи прямокутного паралелепіпеда площинами, паралельними граням і ребрам не прямокутники.
238.
Прямокутний паралелепіпед. Циліндр.
239.
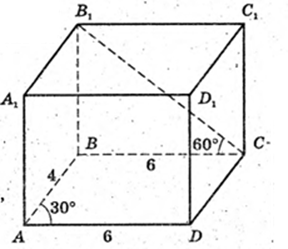
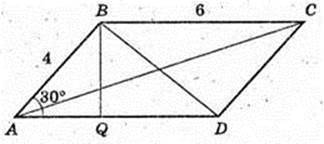
ABCDA1B1C1D1 – прямий паралелепіпед. ABCD – паралелограм.
AB = 4 см, AD = 6 см, ∠ DAB = 30°, ∠ B1CB = 60°.
1) BD – ? AC – ?
ABCD – паралелограм. BQ + AD.
Δ BAQ: ∠ Q = 90°, ∠ A=30°, AB = 4 см → BQ=2 см,
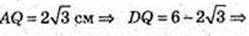
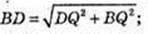
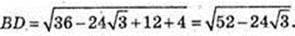
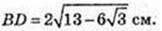
ΔACD: AC2 = AD2 + DC2 – 2AD × DC × cos∠ADC
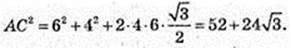
Відповідь: 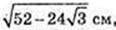
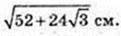
2) H -? H = AA1 – ?
ΔBB1C: ∠B1BC = 90°, ∠B1CB = 60°, ∠BB1C=30°, BC = 6 см → B1C =12 см,
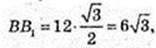
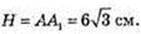
Відповідь: 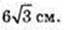
3) B1D – ? AC1 – ?
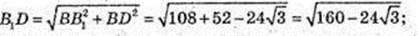
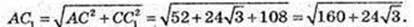
Відповідь: 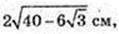
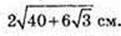
4) ∠C1AC – ? ∠B1DB – ?
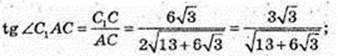
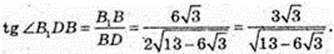
Відповідь: 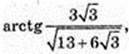
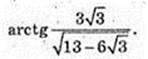
5) ∠AC1C – ?
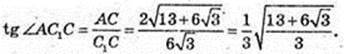
Відповідь: 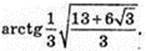
6) SAA1C1C – ? SBB1D1D – ?
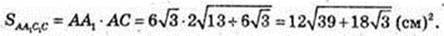
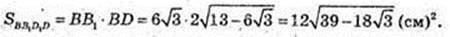
Відповідь: 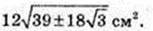
7)
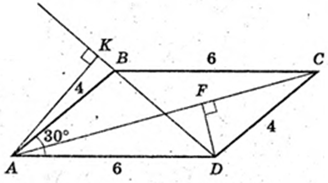
ABCD – паралелограм. AK + BD. AB = 4, AD = 6,
AK – ? DF + AC. DF – ?
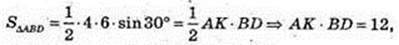
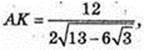
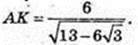
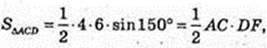
12 = AC × DF, 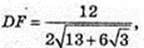
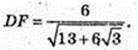
Відповідь: 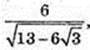
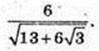
8) ∠C1DC – ? 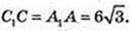 DC = 4.
DC = 4.
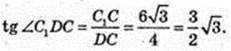
Відповідь: 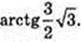
9) SE1E2E3E4 – ? S = 24 см2·
Відповідь: 24 см2.
240 .
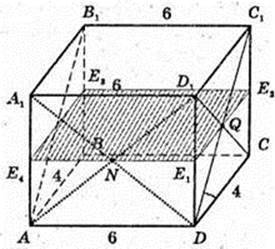
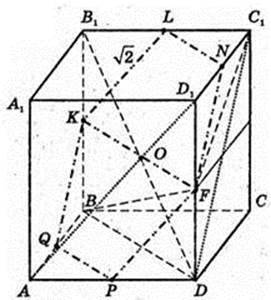
ABCDA1B1C1D1 – прямокутний паралелепіпед.
AB = AD = 1 см, AA1 = H = 2 см.
1)
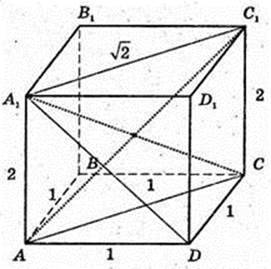
∠A1CA – ? 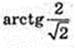 або
або 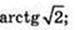
∠CA1D – ? 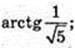
∠CA1B – ? 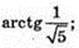
∠A1CB – ? 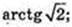
∠CA C1 – ? 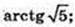
∠A1CCA1 – ? 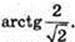
2) ∠CA1A – ? 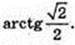
3) S AA1C1C – ? 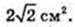
4)d D1DAA1C1C – ? 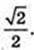
D A1BA1B1CD – ? 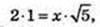
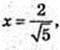
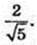
5) 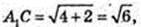
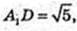
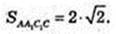
Відповідь: 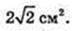
6)
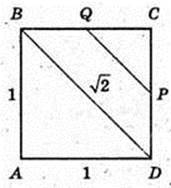
ABCD – квадрат. AB = BC = CD = AD.
AB = 1 см, 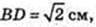
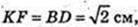
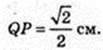
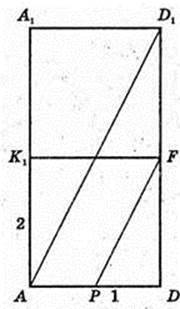
AA1D1D – прямокутник. AD = 1 см, AA1 = 2 см,
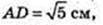
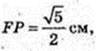
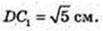
Т. O – центр симетрії паралелепіпеда.
DC1 і AD1 – мимобіжні, діагоналі суміжних граней.
Переріз KLNFPQ, C1D¦ KLNFPQ, AD1¦KLNFPQ.
T. O? KLNFPQ.
S KLNPPQ – ?
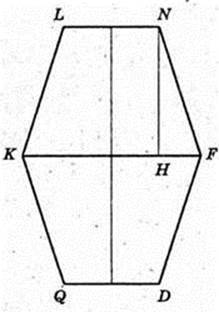
KNMF – трапеція, LN ¦ RN, KL = FN.
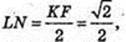
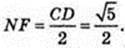
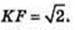
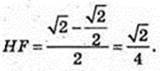
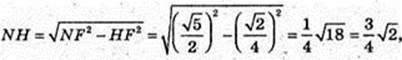
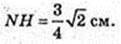
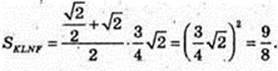
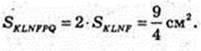
Відповідь: 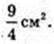
241 .
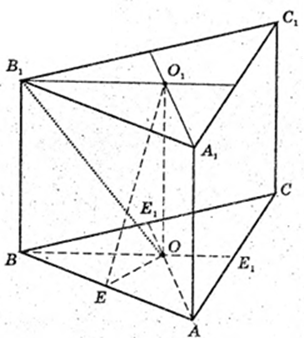
ABCA1B1C1 – правильна трикутна призма.
AA1 = BB1 = CC1= H = 10 см.
AB = BC = AC = 3 см.
1) BO – ?
ΔABC: AB = BC = AC = 3, 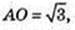
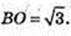
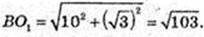
Відповідь: 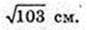
2) O1E – ? O1O = A1A = H = 10. 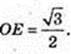
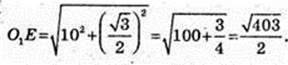
Відповідь: 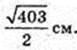
3) ∠B1OC1 – ? 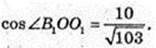
Відповідь: 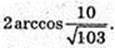
4) SΔAB1C – ? AC = 3 см.
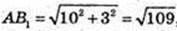
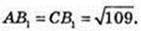
B1E1 – ?
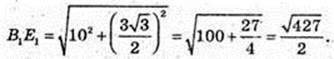
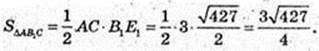
Відповідь: 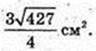
242 .
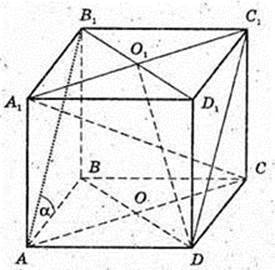
ABCDA1B1C1D1 – правильна чотирикутна призма.
Висота AA1 = Н. ∠B1AB = α.
1) SABCD – ? 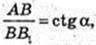 AB = H × ctg α.
AB = H × ctg α.
AB = BC = CD = AD = H ctg α. SABCD = AB2 = H2 × ctg2 α.
Відповідь: H2 ctg2 α.
2) SABCD -? DAB1C1 – прямокутник.
AB1 – ? 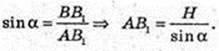
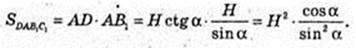
Відповідь: 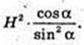
3) ∠A1CC1 – ? ∠D1CB1 – ? ∠A1DC1 – ?
ABCD – квадрат, 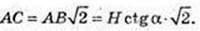
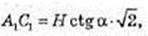 C1C = H.
C1C = H.
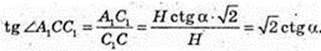
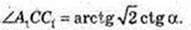
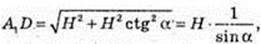
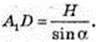
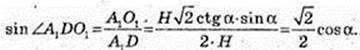
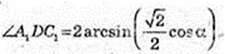
Відповідь: 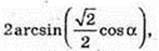
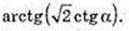
4) SΔA1C1D – ?
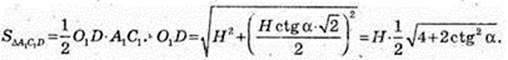
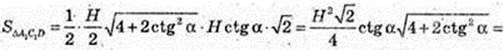
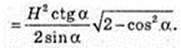
Відповідь: 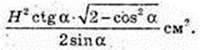
243.
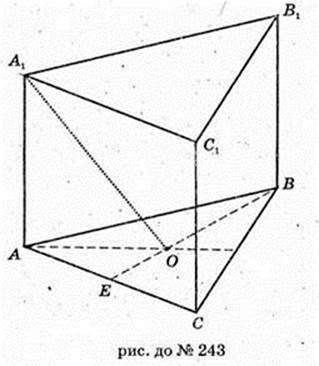
ABCA1B1C, – правильна трикутна призма.
A1O = 4 см. ∠A1OA = 30°. AB – ?
A1A= 2, 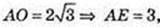 AC = 6.
AC = 6.
Відповідь: 6 см.
244.
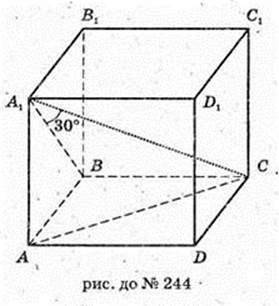
ABCDA1B1C1D1 – правильна чотирикутна призма.
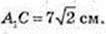 ∠CA1B = 30°. AA1 -?
∠CA1B = 30°. AA1 -?
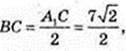 A1B = A1C cos 30°,
A1B = A1C cos 30°,
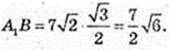
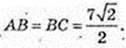
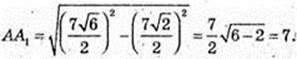
AA1 = 7 см.
Відповідь: 7 см.
245.
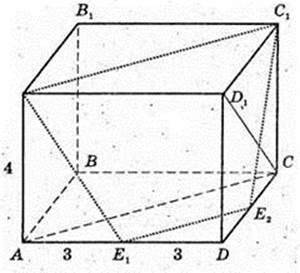
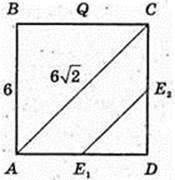
ABCDA1B1C1D1 – правильна призма.
AB= 6 дм, AA1 = 4 дм, E1E2 ¦ АС,
AE1 = E1D, DE2 = E2C. SA1C1E2E1 – ?
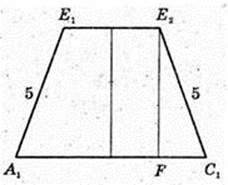
A1E1E2C1 – трапеція, E1E2 ¦A1C1, E1A1 =E2C1
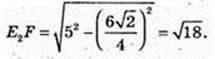
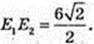
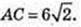
A1E1 = 5 = C1E2.
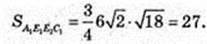
Відповідь: 27 дм2.
246.
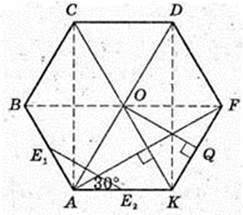
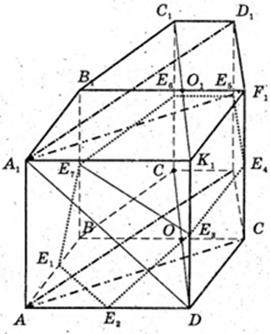
ABCDFK – правильний шестикутник, AB = а.
ABCDFKA1B1C1D1F1K1 – правильна призма.
Переріз BB1F1F такий, що т. O? BB1F1F, т. O1 ? BB1F1F.
BB1F1K – квадрат.
1) AA1 = H – ? AA1 = BF = 2АК = 2а. H = 2а.
Відповідь: 2а.
2) OQ + KF, OQ – ? ΔOFK: OF = FK = OK = а.
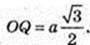
Відповідь: 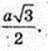
3) SAA1F1F – ? AF – ? AOFK – ромб,
AK = a, ∠AKF = 120°.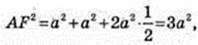
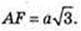
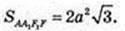
SAA1D1D – ? AD = 2а, SAA1D1D = 2 × 2а2.
Відповідь: 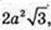 4а2.
4а2.
4) Переріз E1E2E3E4E1E6E7 такий, що AE1 = E1B1 AE2 = E2K.
D1E5 = E5D, F1E4 = E4F, K1E3 = E3K, C1E6 = E6C1 B1E7 = E7B.
E7E3 ¦ E1E2¦BK, E6E4¦BK, E3E4 = KF, E5E4¦DF1, E6E5 ¦ CD1, E7 E6 ¦ BC.
247.
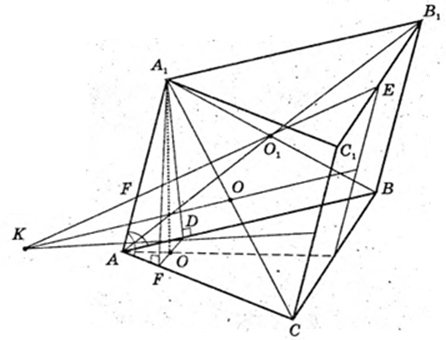
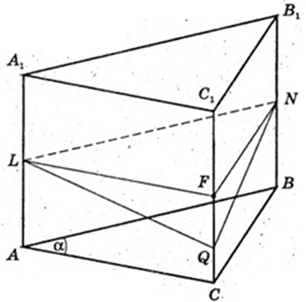
ABCA1B1C1 – похила призма, ΔABC – правильний трикутник.
∠A1AB = ∠CAA1.
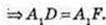
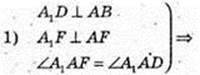
→A1D=A1F,
ΔFAjD: A1O = A1F, A1O + FO = FO = OD, AD =AF.
ΔFAD ∞ ΔCAB → FD ¦ CB, AO + BC.
ПрABC AA1 + BC.
2) AA1 = l, ∠FAA1 = α, ∠DAA1 = α,
A1O = H – ?
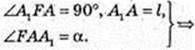
AF = I cos α, A1F = l sin α.
ΔFAD ∞ ΔACAB → AF =AD = FD = I cos α. FD = I cos α,
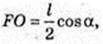
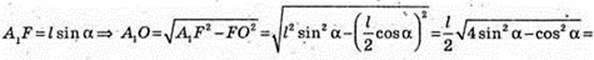
Відповідь: 
248.
ABCA1B1C1 – пряма призма.
1) AA1 + ABC, BB1 + ABC, CC1 + ABC.
Відомо: якщо площина проходить через перпендикуляр до іншої площини,
То ці площини перпендикулярні. AA1C1 + ABC, AA1C1 + A1C1B1.
2)ABCA1B1C1 – правильна призма.
∠ CAB – лінійний
3) 
Кут двогранного кута між гранями CAA1 і BAA1.
4) SLQN = SLFN × cos φ → SLQN ≥ SLFN → SABC → SLQN ≥ SABC.
249.
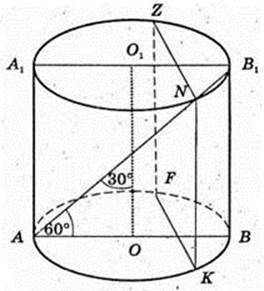
Дано прямий круговий циліндр. AB1 = 20 см, ∠ B1AB = 60°.
1) AO = R – ? Δ AB1B: ∠ B = 90°, ∠ A = 60°,
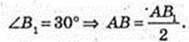 AB = 10, R = AO = 5 см.
AB = 10, R = AO = 5 см.
Відповідь: 5 см.
2) H – ? H = AA1 = BB1
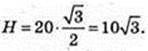
Відповідь: 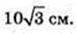
3)SAA1B1B – ? 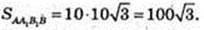
Відповідь: 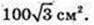
4) ОТ + FK, OT=3 см. FZ ¦ O1O, NF ¦ O1O. SKFZN – ?
OK = R = 5, ОТ = 3 → TK = 4. FK = 8.
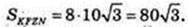
Відповідь: 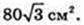
250.
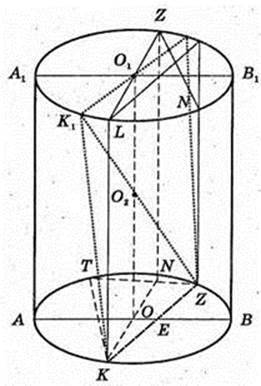
Прямий круговий циліндр. NOKLO1M – квадрат.
1)
KLMN – квадрат.
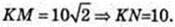
R = KO = S, H = LK=10.
Відповідь: 5 см.
2)
Δ TKZ – правильний. KT – ? KZ = KT – ?
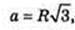
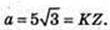
Відповідь: 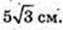
3)
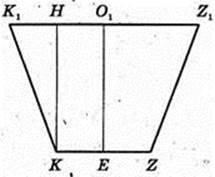
SKK1Z1Z – ? 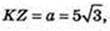
K1Z1 = 2R = 10.
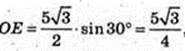
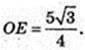
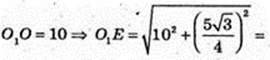
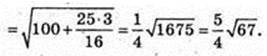
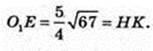
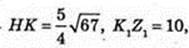
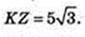
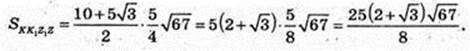
Відповідь: 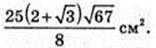
4) 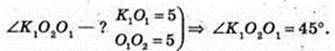
Відповідь: 45°.
5)
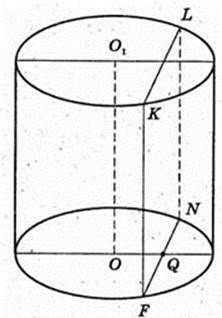
SFKLN – ? KF ¦ O1O, LN = O1O.
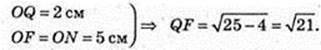
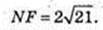 FKLN – прямокутник.
FKLN – прямокутник.
FK = NL = 10. 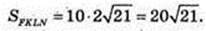
Відповідь: 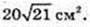
6)
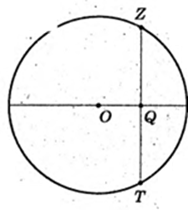
Socн = πR2 = 25π. OQ – ? SFKLN = 25π, FN × KF = 25π.
FN = 2FO, KF = H =10. OQ = X.
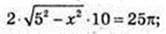
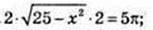
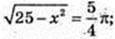
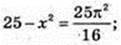
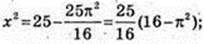
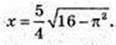
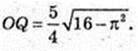
Відповідь: 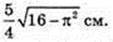
251.
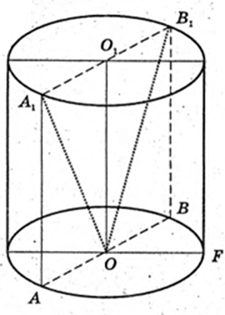
Циліндр прямий круговий; H = AA1 = BB1 = OO1 AO = R.
1) SAA1O1B1BOA – ? S = AB × AA1 = 2RH.
Відповідь: 2RH.
2)
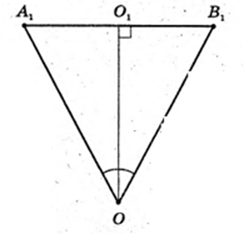
∠A1OB1 – ? A1O1 = R, O1O = H.
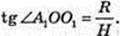
Відповідь·.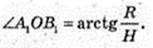
3)
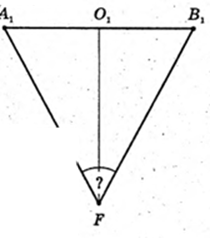
∠A1FB1 – ? A1F – ?
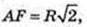
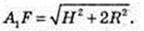
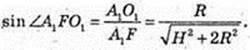
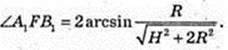
Або 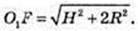
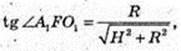
AA1 = H,
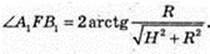
Відповідь: 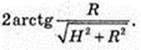
4) AB1 – ? 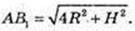
Відповідь: 
252 .
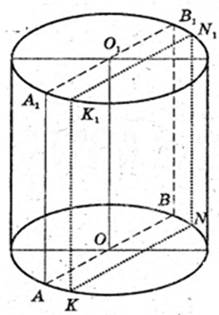
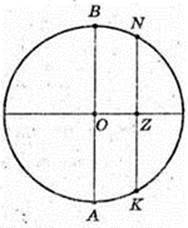
Дано прямий круговий циліндр.
AO = R = 26 см, AA1 = H = 48 см. OZ + NK. OZ – ?
Переріз KK1N1N – квадрат. KN = KK1 = 48 см. KN = 48, KZ=ZN.
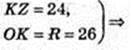
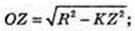
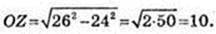
OZ = 10 см.
Відповідь: 10 см.
253.
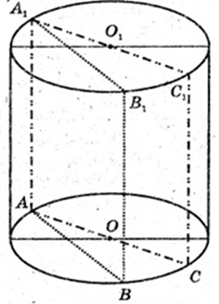
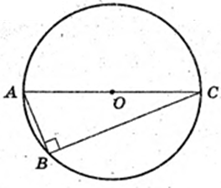
Перерізи AA1O1C1COA і AA1B, В. Знайти ∠ BAC – ?
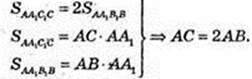
Коло (О, R), AOC = 2R.
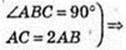
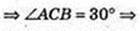
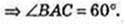
Відповідь: 60°.
254 .
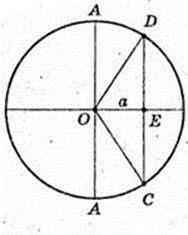
Прямий круговий циліндр. AA1 ? BB1 ? DD1 ? CC1 ? OO1
OO1 = H1 CC1 = H, CD? AB. OE + CD, OE = а. 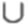 CD = α радіан.
CD = α радіан.
SCC1D1D = S. H – ?
Коло (О, R), OC = OD = R.
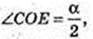 OE = а
OE = а 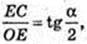
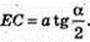
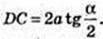
S = DC × Н,
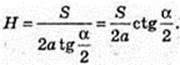
Відповідь: 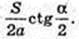
255.
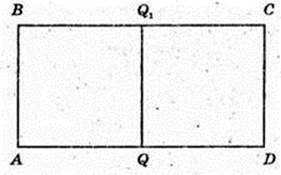
ABCD – прямокутник, SABCD = S.
SABO1FKOA – ?
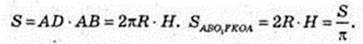
Відповідь: 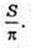
256 .
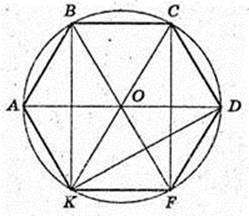
ABCDFK – правильний шестикутник.
1) AD = BF = CK, KD = KB = AC = BD = CF= AF.
2) Діагональ AD, BK + AD, CF + AD,
3) Діагональ KD, KD? АС.
257.
Фігура | Призма | Піраміда | ||||
Кількість | 4-кутна | 5-кутна | N-кутна | 4-кутна | 5-кутна | N-кутна |
Граней | 6 | 7 | N + 2 | 5 | 6 | N + 1 |
Вершин | 8 | 10 | 2n | 5 | 6 | N + 1 |
Ребер | 12 | 15 | 3n | 8 | 10 | 2n |
259.
1) Куб.
2) Піраміда, в основі який знаходиться рівнобедрений трикутник.
3) Правильна трикутна піраміда.
4) Піраміда, основа якої – рівнобедрена трапеція.
5) Прямокутна чотирикутна призма з основою – трикутником.
6) Пряма призма з основою – ромбом.
265.
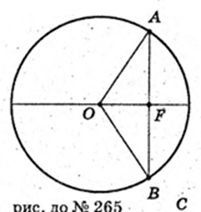
C = 2πR = 10π см ± R = 5 см. Коло (О, Я). AR – хорда,
AB = 8 см. OF+ AB, OF – ?
1) OB = 5, FB = 4 → OF = 3 см.
Відповідь: 3 см.
2) ∠AOB – ? 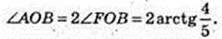
Відповідь: 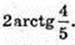
3) OF = 2 см, AB – ?
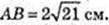
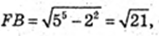
Відповідь: 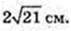
266 .
Коло має центр симетрії – центр кола. Коло має вісь симетрій – пряма, яка перпендикулярна площині кола така, що центр кола належить цієї прямій. Площина, яка проходить через будь – який діаметр кола і перпендикулярна до площини кола є площиною симетрії цього кола.
267.
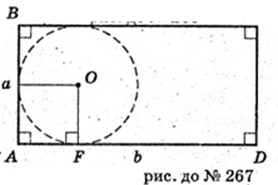
ABCD – прямокутник.
AB = a, AD = b. Якщо Ь > а,
То 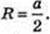
268.
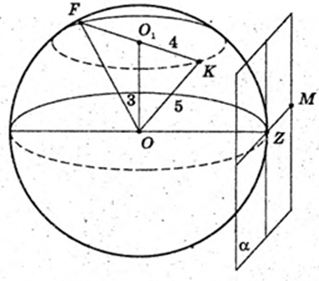
Дана куля (О, r). R= 5 см.
1) O1O = 3 см.
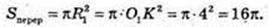
Відповідь: 16π см2.
2)
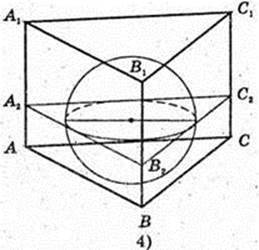
∠FOK – ? 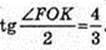
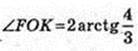
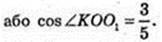
Відповідь: 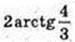 або
або 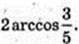
3) Площина α – дотична до кулі, точка Z – точка дотику.
M? α, MZ = 2 см. OM – ?
OZ = R = 5, MZ = 2, 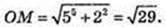
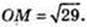
Відповідь: 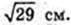
4)
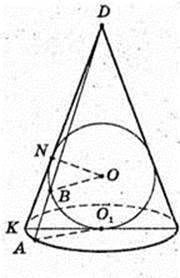
Правильна трикутна призма AA1C1CB описана навколо кулі. AB – ?
R = 5. 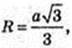
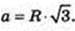
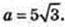
Відповідь: 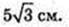
5) Конус описаний навколо кулі, висота конуса DO1 = 12 см.
AO1 = R1 – ?
BO = R = 5. Т. N – точка дотику. ΔDNO – ΔDO1K →
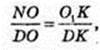 O1K = R1
O1K = R1 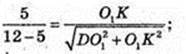
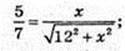 25 × 144 = x2 – 24;
25 × 144 = x2 – 24;
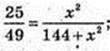 25 × (144 + x2) = 49×2;
25 × (144 + x2) = 49×2; 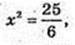
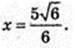
Відповідь: 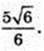
269 .
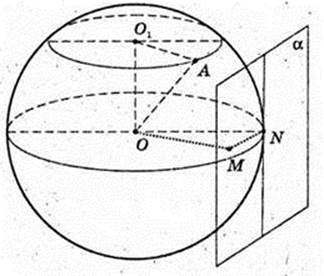
Дана куля (О, R). Переріз — площина, віддалена від центра кулі на 12 см.
1) Sперер.= 25π, R – ? OO1 = 12, OA = R.
πR21 = 25π, R1 = 5, R1 = O1A.
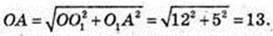
AO = 13. R= 13 см.
Відповідь: 13 см.
2) ∠O1AO – ? 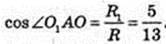
Або 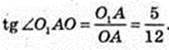
Відповідь: 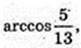
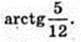
3) Точка N – точка дотику, площина α – дотична, т. M? α, MN = 5см, OM – ?
ΔONM: ∠ONM = 90°, ON = 13, MN = 5, 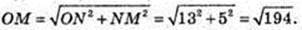
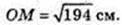
Відповідь: 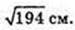
4)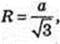
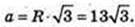
Відповідь: 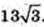
5)
В кулю вписана правильна трикутна піраміда ABCD.
DO1 = 8 см. AB – ?
OC = OD = R= 13, CO1 – ? DO1 = 8 → OO1 = 13 – 8 = 5,
OO1 = 5. ΔOO1C: ∠OO1C = 90°,
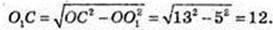 O1C= 12.
O1C= 12.
ΔABC: AB = AC = BC, 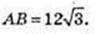
Відповідь: 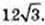
270.
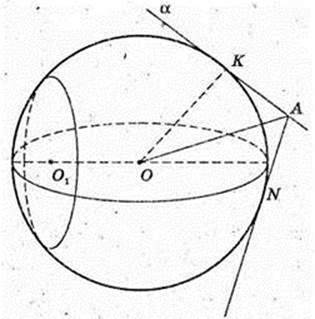
Дана куля (О, R). Пряма l – дотична до кулі, т. K – точка дотику,
Т. A? I, AK = 12 см, R = 5 см, OK = 5 см.
1) OA-: 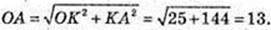 OA= 13 см.
OA= 13 см.
Відповідь: 13 см.
2) Точка N – точка дотику. ∠KAN – ? ∠KAO – ?
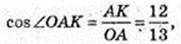
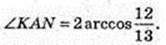
Відповідь: 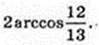
3) S = πR2. Sпеpep = πR2. OO1 – ?
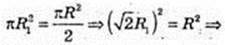
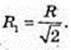
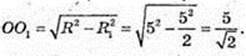
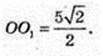
Відповідь: 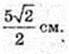
4)
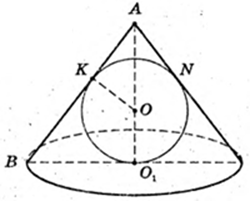
Навколо кулі описано конус з вершиною в т. А.
Точки K i N – точки дотику, BO1 = R – ?
KO = R = 5 см, OO1 = 5 см, OA = 13 см → АО = 18 см.
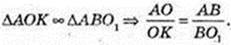
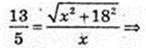
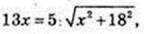
132 × x2 = 25×2 + 52 × 182;
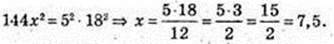
X = BO1 = 7,5 см.
Відповідь: 7,5 см.
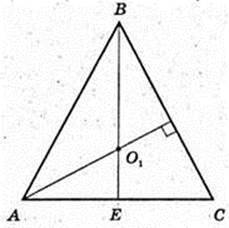
272.
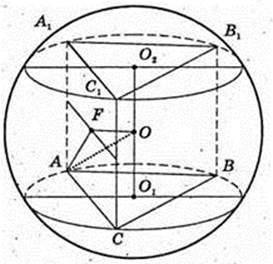
ABCA1B1C1 – правильна трикутна призма.
H = AA2 = 2cм. AB = BC = AC=12см.
1) Описана куля (О, R). R-?
ΔABC: 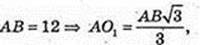
AO1 – ? AB = BC = AC. AB = 12,
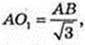
 R = 7 см.
R = 7 см.
Відповідь: 7 см.
2)
Куля вписана в правильну трикутну призму.
OF = R – ?
R = O1O2 : 2 = H : 2 = 1 (см).
Відповідь: 1 см.
3)
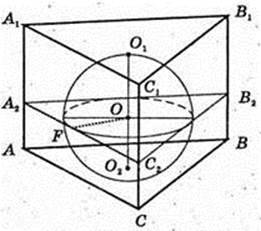
Переріз CC1В1В – коло,
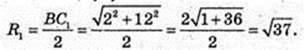
SCC1B1B – ? S = πR2, S = 37π.
Відповідь: 37π см2.
4) OF + AACC1, 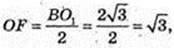
∠OAF – ?
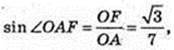
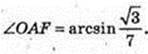
5) ΔA2B2C2, сторони цього трикутника дотикаються до кулі.
A2B2 = 12 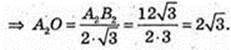
Відповідь: 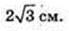
273.
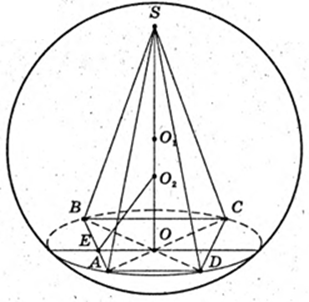
SABCD – правильна чотирикутна піраміда.
AB = BC = CD = a, BD  AC = О. ∠EO = 45°. OE + АВ, SE + AB.
AC = О. ∠EO = 45°. OE + АВ, SE + AB.
SO – висота.
1)
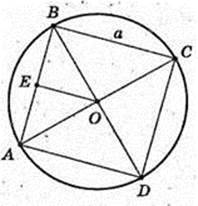
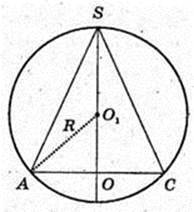
Навколо піраміди описана куля (O1, R) R – ? AO1 = SO1 = R.
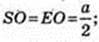
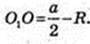
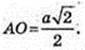
ΔAO1O: ∠AOO1 = 90°,
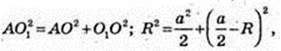
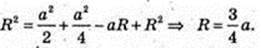
Відповідь: 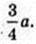
2)
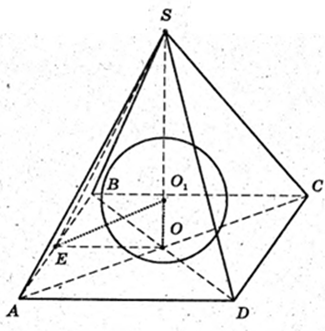
В піраміду вписана куля (O2, r). OO2 = r вп. кулі
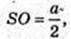 ∠SEO = 45°,
∠SEO = 45°,
EO2 – бісектриса кута SEO.
ΔESO: ∠O = 90°, 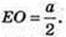
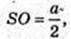
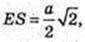
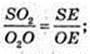
O2O = x. 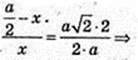
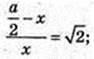
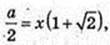
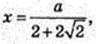
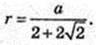
Відповідь:
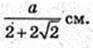
3)
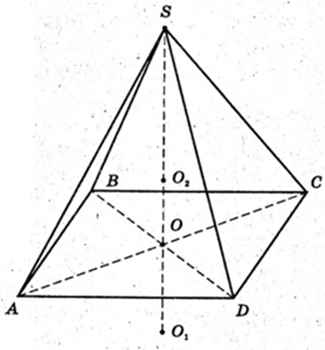
O1O2 – ? т. O1 – центр описаної кулі.
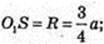
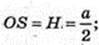 OO2 = r – радіус вписаної кулі.
OO2 = r – радіус вписаної кулі.
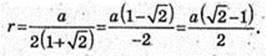
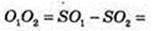
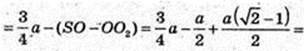
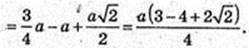
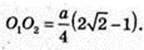
Відповідь: 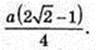
274.
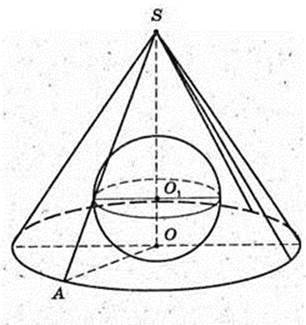
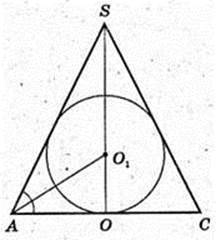
Дано прямий круговий конус, SA = 17 см, SO = H = 15 см.
1) В конус вписана куля (O1, r), дотична конуса і кулі – це коло.
O1O – r? SA = 17 см.
ΔASC: SO + AC, AO = OC, SO = 15 см → OA = 8 см.
AO1 – бісектриса кута
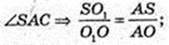
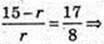
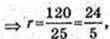
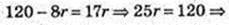
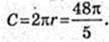
R = 4,8 см.
Відповідь: 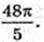
2)
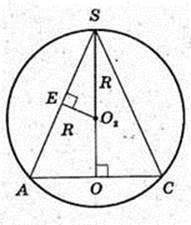
Біля конуса описана куля (O2, R) і в конус вписана куля (O1, r). 
O2S = r, 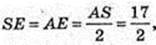
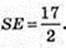 SO = 15.
SO = 15.
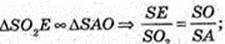
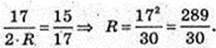
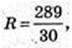
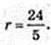
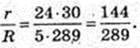
Відповідь: 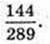
275.
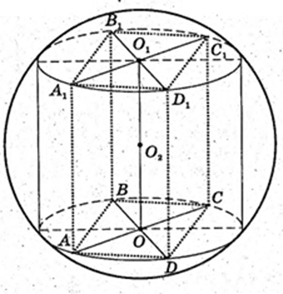
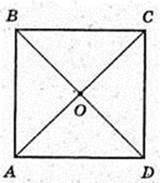
В кулю вписано правильну чотирикутну призму, A1A = a, AB1 = l.
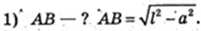
Відповідь: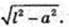
2)
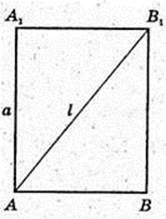
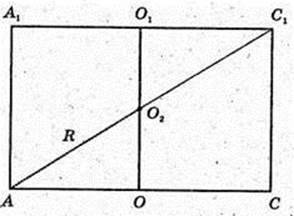
R – ? AA1C1C – прямокутник.
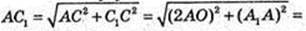
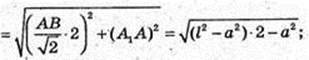
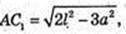
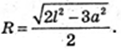
Відповідь: 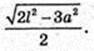
3) ∠C1AC-?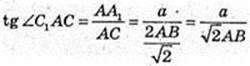
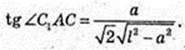
Відповідь: 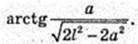
4) ∠B1AB – ?
Відповідь: 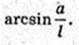
276 .
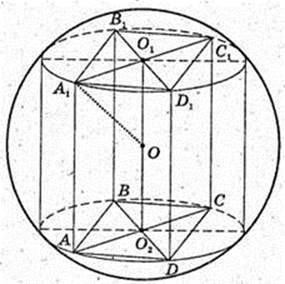
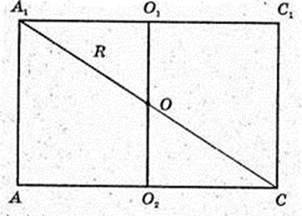
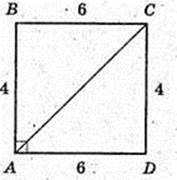
Прямокутний паралелепіпед
ABCDA1B1C1D1 вписаний в кулю (О; R).
AO1 = R. AB = 4 см, AD = 6 см, AA1 = 12 см. R – ? R = A1O – ?
ABCD – прямокутник:
AO2 = O2C, 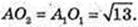 AA1 = 12,
AA1 = 12,
AA1C1C – прямокутник.
ΔA1O1O: ∠O1 = 90°, 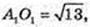
O1O = 6. 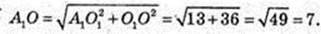
A1O = 7. R = 7.
Відповідь: 7 см.
277.
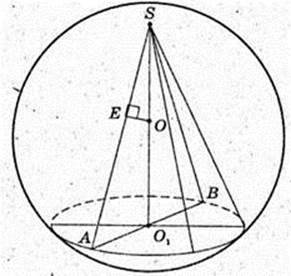
Прямий круговий конус вписано в кулю висота SO1 = 2 см, твірна SA = 4 см.
OA = R – ? OS = R – ?
ΔASB: SA = SB = 4 см, SO1 = 2 см → SE = 2 см.
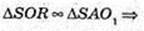
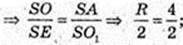 R = 4 см.
R = 4 см.
Відповідь: 4 см.
278.
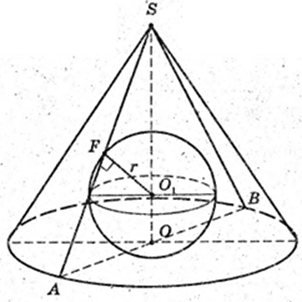
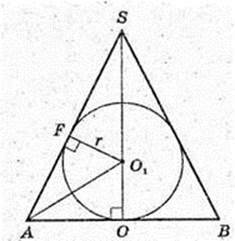
В прямий круговий конус вписана куля (O1, г), висота SO = 8 см, твірна SA= 10 см. O1F + SA, O1F = r – ?
ΔASB: AS = BS = 10, SO = 8.
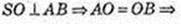
 AO = 6.
AO = 6.
В ΔASB вписано коло (О1, r), точка F – точка дотику, AO1 – бісектриса,
AO = AF = 6 → SF = 4 см. O1F + AS, O1F = г.
Відповідь: 3 см.
279.
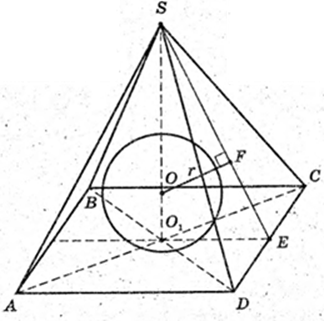
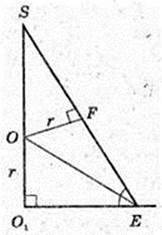
Куля (О, r) вписана в правильну чотирикутну піраміду SABCD.
AS = BS = CS = DS =AB = BC = CD =AD = 2 см. r -?
Точка F – точка дотику кулі і піраміди, OF + SE, DE = CE = 1 см.
ΔDSC: 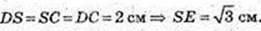
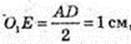
O1E = 1см, OF = r – ?
ΔSEO1: ∠O1 = 90°, O1E = 1, 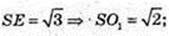
EF = EO1 = 1, 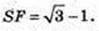
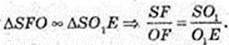
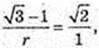
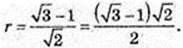
Відповідь: 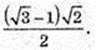
280.
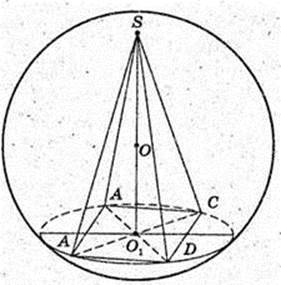
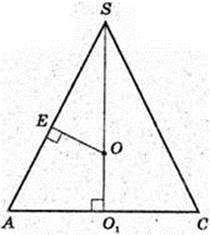
Куля (О, R) описана навколо правильної чотирикутної піраміди SABCD, висота SO1 = 4 см. SA = SB = SC = SD = 6 см. R – ? OS = R – ?
ΔASO1: ∠O1 = 90°, SO1 = 4, AS = 6 см.
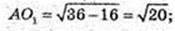
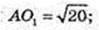
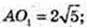 SE = AE, OE + AS, OS = R – ?
SE = AE, OE + AS, OS = R – ?
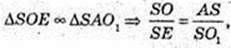
R = 4,5. 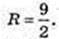
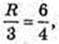
Відповідь: 4,5.
281.
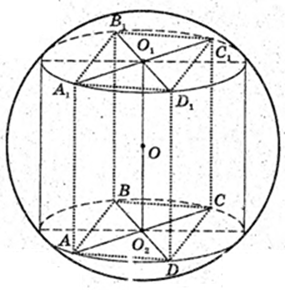
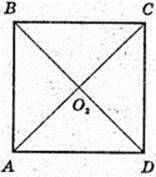
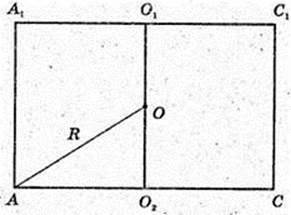
В кулю з радіусом R = 9 см вписана правильна чотирикутна пірамідa
ABCDA1B1CiD1, висота AA1 = 14 см. AB – ?
Δ AOO2: ∠ O2 = 90°, AO = R, 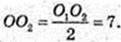
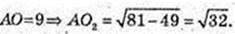
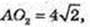
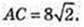
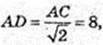 AD = 8 см.
AD = 8 см.
Відповідь: 8 см.
282.
1) ΔАОС: 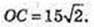
1), 2) Кулька для настільного тенісу поміститься.
283.
Перерізи – коло.
284.
1) Осі симетрії правильного трикутника висоти (медіани, бісектриси).
Осі симетрії ромба – діагоналі його.
Ось симетрії рівнобічної трапеції пряма, яка проходить через середини основ трапеції.
285.
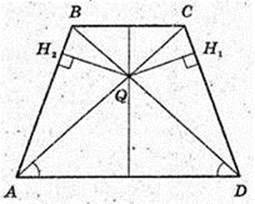
ABCD –рівнобічна трапеція, BC? AD.
Точка Q – точка перетину його діагоналей.
QH1 + CD, QH2 + AB.
ABCD – рівнобічна трапеція → AQ = DQ, BQ = CQ,
∠ AQB = ∠ DQC → ΔABQ = Δ DCQ → QH = QH2.
286.
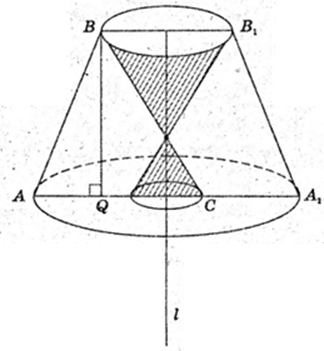
1) Два конуса, у яких спільна основа.
2) Два циліндра.
3) Два конуса, у яких спільна основа.
4) Тор.
5) Два конуса і один зрізаний конус.
287.
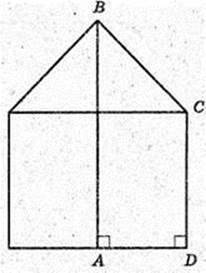
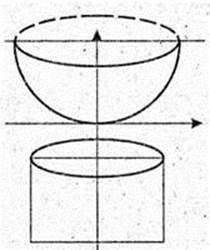
1) прямокутна трапеція обертається навколо більшої її основи.
2) Парабола обертається навколо своєї осі.
3) Прямокутник обертається навколо однієї із своїх сторін.
288.
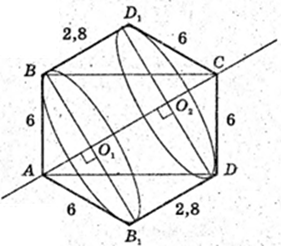
Осьовий переріз фігури обертання – це шестикутник ABD1CDB1
SABD1CDB1 – ?
1) 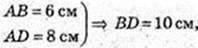 BC = 8 см, AC = 10 см.
BC = 8 см, AC = 10 см.
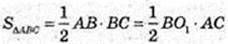 (BO1 + АС).
(BO1 + АС).
6 × 8 = BO1 × 10 → BO1 = 4,8 см = AO1 = 3,6 → O1O2 = 10 = 2 × 3,6 = 2,8;
O1O2 = 2,8; BD1 = 2,8. ABD1C – трапеція.
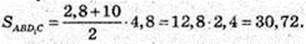
SABD1CDB1 = 2 × SABD1C = 2 × 30,72 = 61,44.
SABD1CDB1 = 61,44 (см2).
Відповідь: 61,44 см2.
2) Перерізи фігури обертання площинами, перпендикулярними до оcі обертання – це кола, найбільший радіус яких дорівнює довжині відрізка BO1,
BO1 = R = 4,8 см. Sперер. = π × 4,82 = 23,04π см2.
Відповідь: 23,04π см2.
