Головна ⇒ 📌Довідник з математики ⇒ Ірраціональні нерівності
Ірраціональні нерівності
Математика – Алгебра
Степенева функція
Ірраціональні нерівності
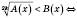
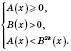
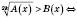
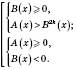
Приклади
1) 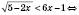
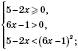
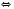
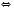
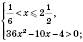
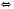
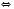
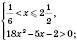
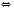
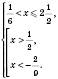
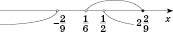
Відповідь: 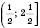 .
.
2) 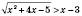
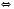
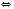
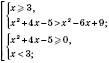
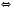
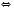
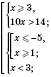
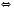
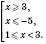

Відповідь: 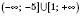 .
.
Related posts:
- Ірраціональні рівняння Математика – Алгебра Степенева функція Ірраціональні рівняння Рівняння, в яких невідоме міститься під знаком кореня, називають Ірраціональними. Розв’язуючи ірраціональні рівняння, намагаються привести їх до вигляду: , або , а потім піднести обидві частини рівняння до n-го степеня. Але якщо піднести обидві частини рівняння до парного степеня, можуть з’явитися сторонні корені. Нариклад: , ОДЗ: ; , […]...
- Логарифмічні нерівності Математика – Алгебра Логарифмічна функція Логарифмічні нерівності Розв’язуючи логарифмічні нерівності, спираються на такі твердження. 1. Якщо , то нерівність рівносильна подвійній нерівності . Це твердження можна записати у вигляді: або 2. Якщо , то нерівність рівносильна подвійній нерівності . Це твердження можна записати у вигляді: або Зверніть увагу: при розв’язуванні логарифмічної нерівності немає сенсу окремо […]...
- Нерівності Математика – Алгебра Нерівності Число а вважається більшим від b, якщо різниця – число додатне. Число a менше від b, якщо різниця – число від’ємне. Якщо , то числа a і b рівні. На координатній прямій меншому числу відповідає точка, що лежить ліворуч від точки, яка відповідає більшому числу. Позначення: – a менше від b; […]...
- Найпростіші ірраціональні рівняння УРОК 37 Тема. Найпростіші ірраціональні рівняння Мета уроку. Познайомити учнів з методами розв’язування ірраціональних рівнянь. Формування умінь розв’язувати ірраціональні рівняння. І. Перевірка домашнього завдання 1. Фронтальна бесіда за запитаннями № 38-46 із “Запитання і завдання для повторення до розділу III”. 2. Розв’язування вправ, аналогічних до домашніх. А) Обчислити . Відповідь: 3. Б) Обчислити . Відповідь: […]...
- Рівняння. Нерівності зі змінною Рівняння. Нерівності зі змінною 1 Розбий записи на дві групи. Назви кожну групу. 27 + х = 51 27 + х < 51 40 ∙ р > 160 2 Згадай, що ти знаєш про рівняння; про нерівності зі змінною. Розглянь, як учні розв’язали рівняння та нерівність способом добору. Прокоментуй їхні дії. Із чисел 1, 2, […]...
- Числові та лінійні нерівності УРОК № 60 Тема. Числові та лінійні нерівності Тестові завдання 1. Яку подвійну нерівність задовольняє множина чисел, поданих на рисунку? А) -4 < x < 8; Б) -4 < х < 8; В) -4 < х < 8; Г) -4 < х < 8. 2. Відомо, що х < у. Яка з наведених нерівностей є […]...
- Нерівності з однією змінною УРОК № 63 Тема. Нерівності з однією змінною Тестові завдання 1. Дано нерівності: 1) -2х2 + х + 6 < 0; 2) 2х2 + х + 7 ? 0; 3) х2 > 0; 4) -3х2 – х – 6 < 0. 2. Яка з даних нерівностей виконується при будь-яких значеннях x? а) усі; б) 2; […]...
- Зростаючі й спадні функції Математика – Алгебра Числові функції Зростаючі й спадні функції Функція називається Зростаючою на деякому інтервалі, якщо для будь-яких двох значень аргументу з цього інтервалу більшому значенню аргументу відповідає більше значення функції. Функція називається Спадною На деякому інтервалі, якщо для будь-яких значень аргументу з цього інтервалу більшому значенню аргументу відповідає менше значення функції. Приклади 1) y […]...
- Найпростіші перетворення радикалів Математика – Алгебра Степенева функція Найпростіші перетворення радикалів 1. Винесення множника за знак радикала Приклади 1) Винесіть множник за знак кореня (, b>0): . 2) Винесіть множник за знак кореня (, ): . Зверніть увагу: , , але , . 3) Винесіть множник за знак кореня : . Даний вираз має зміст при , а […]...
- Степенева функція УРОК 41 Тема. Степенева функція Мета уроку. Познайомити учнів із степеневою функцією, її властивостями і графіками. І. Перевірка домашнього завдання 1. Перевірити наявність виконаного домашнього завдання. 2. Розв’язування вправ. А) Обчислити . Відповідь: 5. Б) Спростити вираз . Відповідь: ab. В) Спростити вираз . Відповідь: 2a. II. Сприймання і усвідомлення матеріалу про степеневу функцію Степеневою […]...
- Лінійні нерівності з однією змінною УРОК № 12 Тема. Лінійні нерівності з однією змінною Мета уроку: домогтися закріплення учнями змісту: означення рівносильних нерівностей та властивостей рівносильних нерівностей; означення лінійної нерівності з однією змінною та схеми Ті розв’язування залежно від різних значень коефіцієнтів. Доповнити знання учнів уявленням про схему дій при розв’язування нерівностей з однією змінною, що містять дроби із числовими […]...
- Функції та графіки Математика – Алгебра Функції та графіки Функція може задаватися описом, таблицею, графіком, формулою тощо. Область визначення функції зручно записувати за допомогою числових проміжків. Приклади 1) ; ; 2) ; ; 3) ; ; 4) ; . Пояснимо, як ми знайшли область визначення в останньому прикладі. Функція визначена для тих і тільки тих значень x, які […]...
- Лінійні нерівності та їхні системи УРОК № 61 Тема. Лінійні нерівності та їхні системи Тестове завдання 1. Знайдіть переріз проміжків (-6; 7] і (-4; 25]. А) [7; 25); б) [-4; 7); в) (-6; 25]; г) (-4; 7]. 2. Розв’яжіть нерівність . A) k < 1,125; б) k? ; в) k? 1,125; г) немає розв’язків. 3. При яких х має зміст […]...
- Раціональні числа, ірраціональні числа, дійсні числа, числові множини, етапи розвитку числа Урок № 37 Тема. Раціональні числа, ірраціональні числа, дійсні числа, числові множини, етапи розвитку числа Мета: систематизувати, узагальнити знання учнів щодо поняття числа та видів чисел, сформувати уявлення про множину дійсних чисел; сформувати вміння учнів відтворювати означення та властивості видів чисел, вивчених на уроці, виконувати найпростіші дії з дійсними числами (зокрема порівняння), використовувати вивчені властивості […]...
- Числові нерівності. Доведення числових нерівностей УРОК № 2 Тема. Числові нерівності. Доведення числових нерівностей Мета уроку: домогтися засвоєння учнями змісту: додаткових нерівностей для суми взаємно обернених додатних чисел та середнього арифметичного двох невід’ємних чисел (у порівнянні з їх середнім геометричним) та доведення цих нерівностей; способу застосування доведених нерівностей при доведенні інших числових нерівностей. Продовжити роботу з вироблення вмінь: відтворювати зміст […]...
- Рівняння. Нерівності зі змінною Мета: узагальнити й систематизувати навчальний досвід учнів відносно рівнянь і нерівностей зі змінною, способів їх розв’язування. Дидактичні задачі. Вдосконалювати навички позатабличного множення та ділення – усна лічба. Класифікувати записи на рівності та нерівності зі змінною. Актуалізувати поняття рівняння, “розв’язок рівняння”, “розв’язати рівняння”; поняття нерівності зі змінною; розуміння способу добору числа для розв’язування рівнянь та нерівностей. […]...
- Парність функції Математика – Алгебра Числові функції Парність функції Функція називається Парною, якщо: 1) ; 2) . У парних функцій протилежним значенням аргументу відповідають рівні значення функції. Графік парної функції симетричний відносно осі Oy. Функція називається Непарною, якщо: 1) ; 2) . У непарних функцій протилежним значенням аргументу відповідають протилежні значення функції. Графік непарної функції симетричний відносно […]...
- Системи нерівностей з однією змінною Математика – Алгебра Нерівності Системи нерівностей з однією змінною Розв’язком системи нерівностей з однією змінною називають значення змінної, яке є розв’язком кожної нерівності даної системи. Розв’язати систему нерівностей означає знайти всі її розв’язки або показати, що їх немає. Щоб розв’язати систему нерівностей, кожну її нерівність поступово спрощують, замінюючи рівносильною. Розглянемо на простих прикладах, як застосувати […]...
- Повторення. Математичні вирази, рівності та нерівності Повторення. Математичні вирази, рівності та нерівності 1 Розбий математичні вирази на дві групи. Прочитай математичні вирази різними способами. 420 + 350 618 – а х + у 920 – 460 7 ∙ с 151 ∙ 4 408 : 3 n : 14 Значення яких виразів ти можеш знайти? Знайди їх значення. Чого не вистачає, щоб […]...
- Властивості числових нерівностей Математика – Алгебра Нерівності Властивості числових нерівностей a, b, с, d – довільні числа. 1. Якщо і , то . 2. Якщо до обох частин правильної нерівності додати одне й те саме число, то дістанемо правильну нерівність. 3. Якщо обидві частини правильної нерівності помножити на одне й те саме додатне число, то дістанемо правильну нерівність. […]...
- Показникові рівняння Математика – Алгебра Степенева функція Показникові рівняння Показниковими рівняннями називають такі рівняння, в яких невідоме входить лише до показників степенів при сталих основах. Розв’язування показникових рівнянь 1. Розв’язування зведенням до спільної основи , , , , , x = ±2. Відповідь: x1 = 2; x2 = -2. 2. Показникові рівняння, що мають показники з однаковою […]...
- ЧИСЛОВІ ВИРАЗИ, РІВНОСТІ, НЕРІВНОСТІ. ПОРІВНЯННЯ НАТУРАЛЬНИХ ЧИСЕЛ РОЗДІЛ 1 ЛІЧБА, ВИМІРЮВАННЯ І ЧИСЛА § 4. ЧИСЛОВІ ВИРАЗИ, РІВНОСТІ, НЕРІВНОСТІ. ПОРІВНЯННЯ НАТУРАЛЬНИХ ЧИСЕЛ Ви вже знаєте чотири арифметичні дії над числами – додавання, віднімання, множення і ділення. Щоб записати, яку саме дію над числами треба виконати, використовують числові вирази. Наприклад, записи 24 + 2, 24 – 2, 24 ∙ 2, 24 : 2 […]...
- РОЗВ’ЯЗУВАННЯ ТА СКЛАДАННЯ ЗАДАЧ НА ПРОПОРЦІЙНЕ ДІЛЕННЯ. РІВНЯННЯ І НЕРІВНОСТІ ОРІЄНТОВНА НАВЧАЛЬНА МЕТА: ЗАКРІПЛЮВАТИ ВМІННЯ СКЛАДАТИ ЗАДАЧІ НА ПРОПОРЦІЙНЕ ДІЛЕННЯ; ДОСЛІДИТИ МОЖЛИВОСТІ ПЕРЕБУДОВИ ЗАДАЧ НА ЗАДАЧІ НА ПРОПОРЦІЙНИЙ ПОДІЛ I. Перевірка домашнього завдання Фронтально скласти план розв’язування задачі 847. Взаємоперевірка обчислення виразів вправи 848. II. Актуалізація та корекція опорних знань учнів 1. Усні обчислення. Змагання двох команд гравців. 1 команда 2 команда 350 • (430 […]...
- Розв’язування нерівностей з однією змінною Математика – Алгебра Нерівності Розв’язування нерівностей з однією змінною Розв’язком нерівності з однією змінною називається значення цієї змінної, яке перетворює її на правильну числову нерівність. Розв’язати нерівність означає знайти всі її розв’язки або довести, що їх немає. Дві нерівності називають Рівносильними, якщо вони мають одні й ті самі розв’язки або не мають розв’язків. Числові проміжки […]...
- Основні теореми про границі функцій Математика – Алгебра Границя Основні теореми про границі функцій Теорема 1. Якщо функції і в точці мають границі, то сума і добуток цих функцій також мають у цій точці границю, причому ; . Теорема 2. Якщо функції і в точці мають границі й , то й функція має в цій точці границю, яка дорівнює . […]...
- Дійсні числа Математика – Алгебра Квадратні корені Раціональні числа – це числа, які можуть бути записані у вигляді , де m – ціле число, n – натуральне. Кожне раціональне число можна подати у вигляді нескінченного періодичного десяткового дробу. І навпаки, кожний нескінченний періодичний десятковий дріб є раціональним числом. Числа, які зображуються нескінченними неперіодичними десятковими дробами, називають ірраціональними. […]...
- Контрольна робота № 7 (підсумкова) УРОКИ 63-70 Уроки 63-70 відповідають V розділу програми з алгебри та початків аналізу “Резерв навчального часу”, і вчитель може використовувати цей час на власний розсуд з урахуванням рівня математичної підготовки учнів. Ці години можна використати на повторення на початку навчального року, як додаткові години на окремі теми або для узагальнення й систематизацію матеріалу і повторення […]...
- Приклади розв’язування системи тригонометричних рівнянь Математика – Алгебра Тригонометричні функції Приклади розв’язування системи тригонометричних рівнянь 1) Відповідь: , n Є Z; , n Є Z. 2) а) б) Відповідь: , n, k Є Z; , n, k Є Z....
- НЕРІВНОСТІ ТРИКУТНИКА РОЗДІЛ 3 ТРИКУТНИКИ & 15. НЕРІВНОСТІ ТРИКУТНИКА Ви вже знаєте, що кожна сторона трикутника менша від суми двох інших його сторін. Щоб довести це твердження як теорему, спочатку розглянемо іншу теорему. Теорема 19 У кожному трикутнику проти більшої сторони лежить більший кут, а проти більшого кута – більша сторона. Доведення. 1) Нехай у трикутнику ABC […]...
- Узагальнення поняття степеня Математика – Алгебра Степенева функція Узагальнення поняття степеня Основнi означення 1. Якщо n Є N, , то , де a – довільне число. 2. , де а – довільне число. 3. для . не має змісту. 4. , n Є N, . 5. , n Є N, m Є Z, . Властивості степеня з раціональним […]...