Коло
Геометрія
Основні властивості найпростіших геометричних фігур
Коло
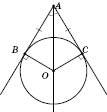
Колом називається фігура, яка складається з усіх точок площини, рівновіддалених від даної точки. Ця точка називається Центром кола.
Відстань від точок кола до його центра називається Радіусом кола. Радіусом також називається будь-який відрізок, що сполучає точку кола з його центром.
Відрізок, що сполучає дві точки кола, називається Хордою. Хорда, що проходить через центр кола, називається Діаметром.
На рисунку зображено коло з центром у точці O. OA –
Теорема 1. Діаметр, перпендикулярний до хорди, ділить її навпіл.
Теорема 2. Діаметр, який проходить через середину хорди, перпендикулярний до неї.
Серединним перпендикуляром до відрізка називається пряма, що проходить через середину відрізка перпендикулярно до нього.
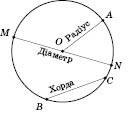
Коло називається Описаним навколо трикутника, якщо воно проходить через усі його вершини.
Теорема 3. Навколо будь-якого трикутника можна описати коло. Його центр – точка перетину серединних перпендикулярів до сторін трикутника.
Зверніть увагу: у гострокутному
Дотична до кола
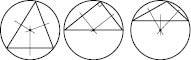
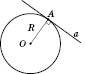
Пряма, що проходить через точку кола перпендикулярно до радіуса, проведеного в цю точку, називається Дотичною. Дана точка кола називається Точкою дотику.
Теорема 1. Дотична до кола має з ним єдину спільну точку – точку дотику.
На рисунку a – дотична.
Якщо два кола, які мають спільну точку, мають у ній спільну дотичну, кажуть, що ці Кола дотикаються. Дотик кіл називають Внутрішнім, якщо центри кіл лежать по один бік від їх спільної дотичної (рисунок нижче зліва), і Зовнішнім, якщо центри кіл лежать по різні боки від спільної дотичної (рисунок справа).
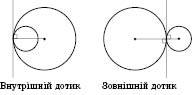
Коло називається Вписаним у трикутник, якщо воно дотикається до всіх його сторін.
Теорема 2. У будь-який трикутник можна вписати коло. Центр кола, вписаного в трикутник, є точкою перетину його бісектрис.
Теорема 3. Із будь-якої точки поза колом можна провести до кола дві дотичні. Відрізки цих дотичних від даної точки до точок дотику рівні. Промінь, що виходить із даної точки й проходить крізь центр кола, є бісектрисою кута між дотичними.
На рисунку нижче AB і AC – дотичні. Теорема стверджує, що AB = AC; AO – бісектриса 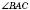 .
.