Конус і зрізаний конус
983.
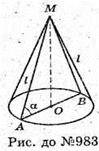
Нехай дано конус, твірна якого AM = l, і нахилена до площини основи під кутом ∠MAO = α.
А) ΔAMO – прямокутний. OM – висота, OM = l × sin α;
Б) AO – радіус основи конуса. AO = l × cos α;
В) ΔAMB – осьовий переріз;
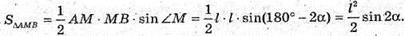
Г) площа основи конуса – площа круга. Sкр. = π × R2= π × AD2.
Sкр.= π × l2 cos2α.
984.
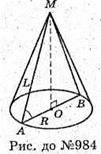
Нехай дано конус, площа основи – S. Площа поверхні 3S.
∠MAO – кут нахилу твірної до площини основи.
Sб. = πRL, Sп. = Sб. +
3S = πRL + πR2; πR(L + R) = 3πP2; L+ R = 3R; L = 2R.
ΔMAO – прямокутний. AO = R; AM = 2R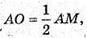
отже, катет, що лежить навпроти кута 30°, дорівнює половині гіпотенузи. ∠MAO = 60°.
Відповідь: 60°.
985.
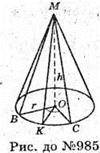
Нехай дано конус, висота якого MO = h, OB = r – радіус основи конуса.
ΔMBC – переріз, який проходить через вершину конуса і хорду основи, що стягує дугу 60°, це означає, що центральний кут ∠BOC = 60°.
ΔBOC – рівносторонній. OB = OC = BC = r.
ΔMBC – рівнобедрений, MK + BC; BK = KС.
ΔOBK – прямокутний, OK + ВС;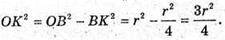 
ΔMOK
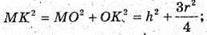
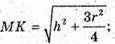
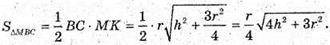
Відповідь: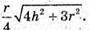 
986.
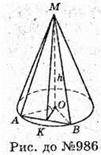
Нехай дано конус, в якому через вершину M проведено площину МАВ, що відтинає від кола дугу AB = 90° (∠AOB = 90°) і нахилена до площини основи під кутом ∠MKO = 60°. MO + пл. основи, OK + AB, отже, MK + АВ, ∠MKO – лінійний кут двогранного кута при ребріAB.
ΔAMB – кут при вершині перерізу.
Нехай AO = R, тоді з ΔАОK: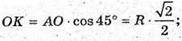 
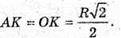
ΔМОK – прямокутний.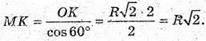 
ΔMAK – прямокутний. AM2 = MK2 + AK2;
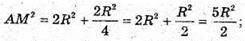
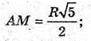
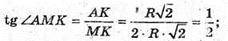
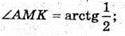
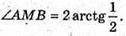
Відповідь: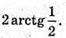 
987.
Нехай дано розгортку бічної поверхні конуса – круговий сектор з дугою 90°. ∠AOB = 90°. Нехай OA = OB = R – радіус сектора:
А)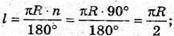 
l – довжина дуги АВ. AO = OB = L – твірна конуса, l довжина кола основи конуса. l = 2πR1, де R1- радіус основи конуса.
AO1 = R1;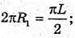 
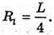
ΔAOO1- прямокутний.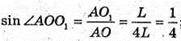 
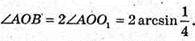
Б) дуга дорівнює 180°. Довжина дуги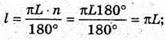 
2πR1 = πL;
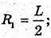
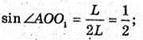∠AOO1 = 30°; ∠AOB = 2 ∠AOO1 = 60°;
В) дуга дорівнює 270°.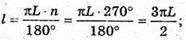 
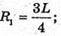
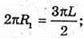
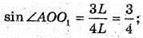
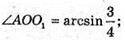
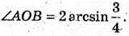
Відповідь: а)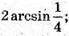 
б) 60°; в)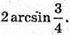 
988.
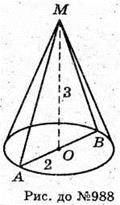
Нехай дано конус з висотою MO = 3м і діаметром AB = 4м.
Sб. = πRl; S б. = π × 2 × l.
ΔMOA – прямокутний.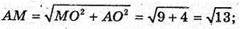 
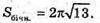
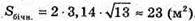
989.
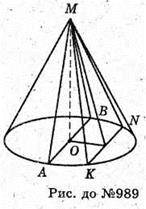
Нехай дано зрізаний конус, O1A = 3 дм; O2B = 6 дм; AB = 5 дм.
A) AF – висота; BО2 – A1O1 = BF = 6 – 3 = 3 (дм).
ΔAFB: AF2 = AB2 – BF2; AF2 = 25 – 9 = 16; AF = 4. Висота AF = 4;
Б) ΔBCD – осьовий переріз конуса – трапеція.
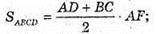
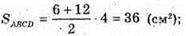
В) ∠B = а – кут нахилу твірної до площини основи.
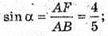
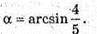
Відповідь: 4 дм; 36 дм2; arcsin 0,8.
990.
Нехай дано зрізаний конус, радіуси основ конуса R і r, а твірна AB утворює кут α з площиною основи.
Sбічн. зр. конуса = πl(R + r).
BK = O2B – O1A = R – r
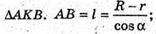
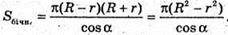
Відповідь: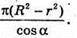 
991.
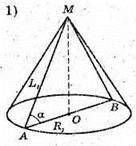
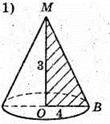
А) Нехай прямокутний ΔMOB обертається навколо катета MO = 3 см;
Sб. = πRl. Sосн. = πR2. Sповерхні = πRl + πR2 = πR(l + R);
Sповерхні = π × 4(5 + 4) = 36π (см2);
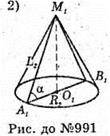
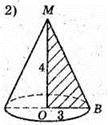
Б) Нехай прямокутний ΔMOB обертається навколо катета MO = 4 см
Sповерхні = πR(R + l). Sповерхні = π × 3(5 + 3) = 24π (см2);
В) Нехай прямокутний трикутник обертається навколо гіпотенузи
Sповерхні = Sб. конуса1 + Sб. конуса2. Sб. конуса1 = π × MO × KО.
Sб. конуса2 = π × OB × KО.
S поверхні = π × MO × KO + π × OB × KO = π × KО(МО + ОВ),
Де MO = 3 см; OB = 4 см;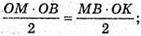 
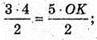
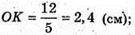
S поверхні = π × 2,4(3 + 4) = 16,8π (см2).
992.
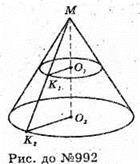
Нехай рівнобедрений прямокутний ΔABC обертається навколо, прямої І, проведеної через вершину прямого кута, паралельно гіпотенузі. BC = AC = а.
Площа поверхні тіла обертання дорівнює сумі площі бічної поверхні циліндра з радіусом OA і твірною AB та площі бічної поверхні двох, конусів з радіусом OA і твірною АС.
S поверхні = 2πRl + 2πRl1, де R = OA, l = АВ, l1 = ВС,
З прямокутного трикутника ABC: BC = AC = а;
AB2 = а2 + а2 = 2а2;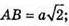 
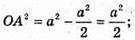
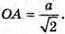
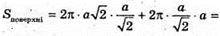
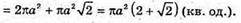
Відповідь: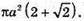 
993.
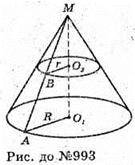
Нехай ABCD прямокутна трапеція з основами AB = 2 см і DC = 6 см; AD = 3 см.
А)
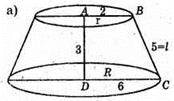
Нехай прямокутна трапеція обертається навколо меншої бічної сторони. Поверхня тіла обертання дорівнює:
Sбiчн. зріз. конус. + 2Sосн. × S поверхні= πl(R + r) + πR2 + πr2;
S поверхні = 5π(2 + 6) + 4π + 36π = 40π + 4π + 36π = 80π (см2).
Б)
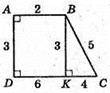
Нехай прямокутна трапеція обертається навколо більшої основи.
AD = 6 см; BC = 2 см; DC = 5 см; AB = 3 см; OD = 4 см.
Площа поверхні дорівнює сумі бічної площі поверхні конуса і бічної поверхні циліндра та площі основи циліндра.
S поверхні = π × OC × DC + 2π × OC × BC + π × OC2= π × OC(DC + 2 BC + ОС) =
= π × 3(5 + 2 × 2 + 3) = 3π ×12 = 36π(см2).
В)
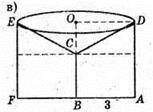
Площа поверхні дорівнює сумі площ бічної поверхні циліндра, площі основи циліндра і бічної поверхні конуса.
Sпов. = 2π × AB × AD + π × AB2 + π × AB × CD = 2π × 3 × 6 + π × 9 + π × 3 × 5 =
= 36π + 9π + 15π = 60π (см2).
Відповідь: a) 80π; 6) 36π; в) 60π.
994.
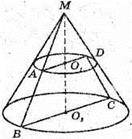
ΔAMB – осьовий переріз конуса. PΔAMB = AM + MB + АВ. PΔKMN = KM + NM + KN.
AB – діаметр – найбільша хорда, отже з усіх перерізів конуса площинами, які проходять через вершину, найбільший периметр має осьовий переріз.
995.
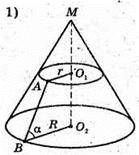
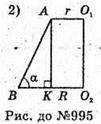
3 усіх перерізів конуса площинами, які проходять через вершину, найбільшу площу має осьовий переріз.
996.
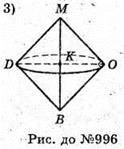
Нехай твірні, двох конусів нахилені до площини основи під рівними кутами.
ΔMОA. MO = AM × sin α. ΔM1A1O1. M1O1 = A1M1 × sin α.
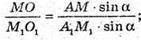
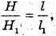Отже, якщо твірні двох конусів нахилені до площин основ від рівними кутами, то висоти цих конусів відносяться як твірні, що й треба було довести..
S1бічн. = πR1L1; S2бічн. = πR1; L1 = R 1 cos α; L2 = R2 × cos α·
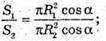
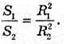
Площі бічних поверхонь відносяться як квадрати радіусів основ конусів.
997.
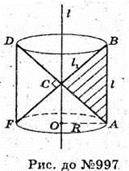
Нехай дано конус, в якому MO1 – відстань січної площини від вершини конуса. O2M – відстань від площини основи до вершини конуса.
Нехай O2K2= R2,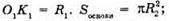 
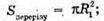
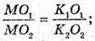
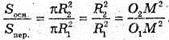
Отже, доведено, що площі основи конуса і його перерізу площиною, паралельною основі, відносяться як квадрати відстаней цих площин від вершини конуса.
998.
Нехай висота конуса MO1= h. Sпер. = πr2, Sосн. = πR2.
Нехай O2 B = r; O1A = R.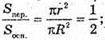 
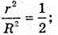
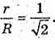
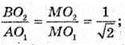
ΔBMO2 – ΔAMO1.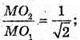 
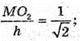
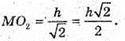
Відповідь: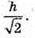 
999.
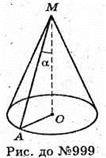
Нехай дано конус, AM – твірна, MO – висота, MA – MO = a, ∠AMO = α.
Нехай твірна AM = l, тоді AO = l sin α; OM = l cos α.
За умовою l – l cos α = а; l(l – cos α) = а;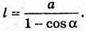 
ΔАМО.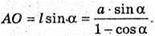 
Площа бічної поверхні конуса:
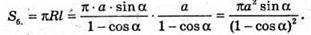
Відповідь: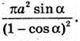 
1000.
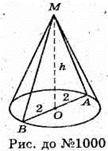
Нехай дано конус, радіус основи якого 2 см, площа бічної поверхні конуса дорівнює сумі площ основи осьового перерізу.
S б. к. = Sосн. + S ΔABM
Нехай MO2 = h.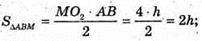 
S осн. = π · r2 = 4π;
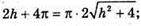
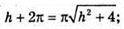(h + 2π)2 = π2(h2 + 4);
H2 + 4πh + 4π2= π2h2 + 4π2; π2h2- h2= 4πh; h2(π2 – 1). = 4πh;
H(π2 – 1) = 4π;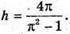 
Відповідь: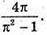 
1001.
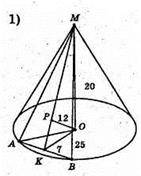
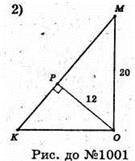
Нехай дано конус, висота якого 20 см, радіус основи 25 см. Через вершину конуса проведено площину (МАВ) на відстані OP = 12 см від центра основи.
OP + (МАВ), OP + МK.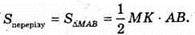 
ΔMPO – прямокутний. MP2 = MO2 – OP2 = 400 – 144 = 256; MP = 16.
MO2= MK × МР, 400 = MK × 16;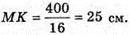 
OK2= MK2= MO2 = 625 – 400 = = 225, OK = 15.
ΔOKB – прямокутний. BK2 = OB2 – OK2 = 625 – 225 = 400; BK = 20; AB = 40.
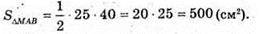
Відповідь: 500 см2.
1002.
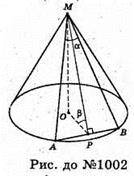
Нехай дано конус, через дві твірні конуса проведено площину (AMB), яка утворює з площиною основи ∠MPO = β. MO + пл. основи; OP + АВ, MP + AB,
∠MPO – лінійний кут двогранного кута при ребрі AB. ∠AMB = α, кут між двома твірними конуса. SΔAMAB = S. MO – висота конуса.
ΔMAP – прямокутний.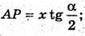 
Нехай MP = х,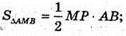 
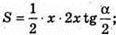
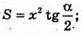
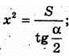
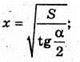
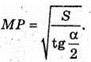
ΔMOP – прямокутний. ∠MOP = 90°;
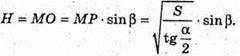
Відповідь:
1003.
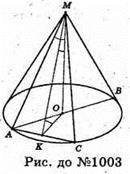
Нехай дано конус, осьовий переріз якого ΔАМВ. Через вершину конуса проведено площину (AMC) під кутом 60° до його площини основи.
MO + площині основи. OK + АС, MK + AC. ∠MKO = 60° (лінійний кут двогранного кута АС).
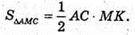
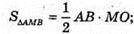
Нехай OM = h, тоді AO = R;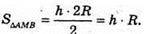 
ΔMOK.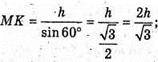 
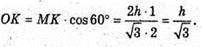
ΔАОK.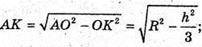 
. 
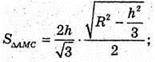
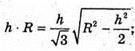
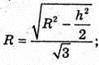
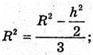
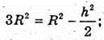
6R2= 2R2 – h2; 4R2 =h2;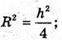 
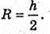
ΔАМО.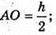 
MO = h;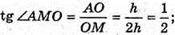 
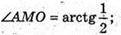
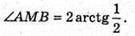
Відповідь: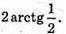 
1004.
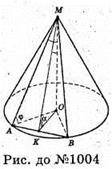
Нехай дано конус, через вершину конуса M проведено переріз конуса площиною МАВ. MO + площині, основи. OK + АВ, MK + АВ. ∠MKO = α. ∠MKO – кут між площиною перерізу (МАВ) і площиною основи.
∠MAO = φ -: кут, який утворює похила MA з площиною основи. MA – твірна конуса. Повна поверхня конуса Q. Sповне = πR2 + πR × 4 = πR(R + L), де R – радіус основи конуса, L – твірна конуса.
Нехай AO = R, тоді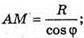 
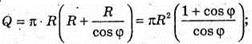
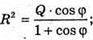
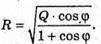
ΔAOM – прямокутний.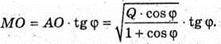 
ΔMOK – прямокутний.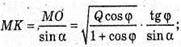 
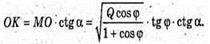
ΔAKO – прямокутний.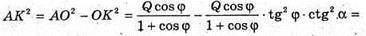 
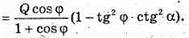
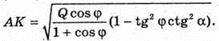
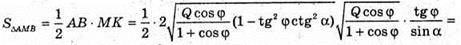
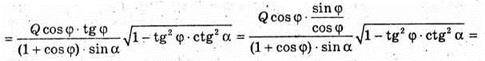
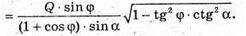
1005.
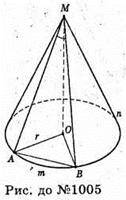
Нехай дано конус, AM і MB – твірні, AM + MB, ∠AMB = 90°.
AO = OB = r – радіуси основи конуса.
S1 : S1 : 2 – площі бічної поверхні конуса, на які вони діляться твірними.
S б. = π × R × L.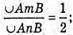 
360°; 3 = 120°; ∠AOB = 120°.
ΔAOB – рівнобедреник. AO = OB = r; ∠AOB = 120°;
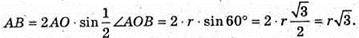
ΔAMB – прямокутний рівнобедрений. ∠AMB = 90°.
AM2 + BM2 = AB2; 2AM2 = 3r2;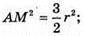 
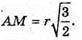
ΔAOM – прямокутний. OM2 = AM2 – AO2за теоремою Піфагора.
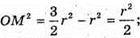
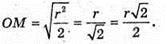
Відповідь: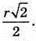 
1006.
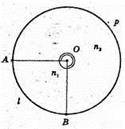
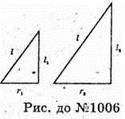
Нехай круг поділили на 2 сектори.
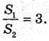
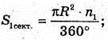
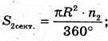
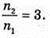
N2 = Зn1; n1 + 3n1 = 360°; 4n1 = 360°; n1 = 90°; n2 = 270°.
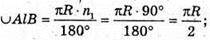
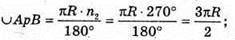
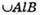– довжина кола основи першого конуса.
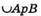– довжина кола основи другого конуса.
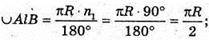
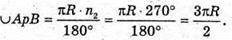
R = l – твірні конусів. У даних конусів твірні рівні.
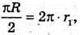де r1 – радіус основи першого конуса.
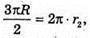де r2 – радіус основи другого конуса.
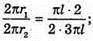
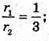І = І. 
Відповідь: 
1007.
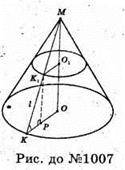
Нехай дано зрізаний конус, твірна якого K1K нахилена до площини основи під кутом α. K1K = l. ∠K1KO = α. K1P + площині основи. K1K – похила, KO – її проекція.
S1 : S2 = 1 : 4, де S1 – площа першої основи, S2- площа другої основи конуса.
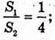
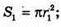
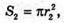де r1 = O1K1; r2= ОK;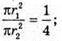 
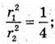
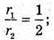
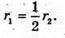
ΔKK1P – прямокутний. K1P = K1K × sin α = l × sin α; KP = K1K × cos α = l × cos α.
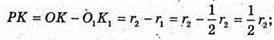r2 = 2PK = 2l cos α;
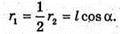Sповна = Sоснови1 + Sоснови2 + Sбічн. зріз. конуса
Sоснови1 = π × r12 =πl2 cos2 α; Sоснови2 = π × r22 =πl2 cos2 α;
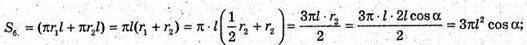
S повна конуса = πl2 cos2α + 4πl2 cos2α + 3πl2 cos α = 5πl2 cos2α + 3πl2 cos α =
= πl2 cos α × (5 cos α + 3).
Відповідь: πl2 cos α(5 cos α + 3).
1008.
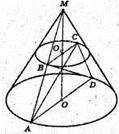
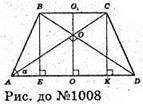
Нехай дано зрізаний конус, в якого діагоналі осьового перерізу взаємно перпендикулярні.
AC + BD. Твірна AB = l і утворює із площиною кут BAO = α.
Площа бічної поверхні дорівнює:
Sбічна зрізаного кола = πl(R + r), де l = AB, r = AO, r = O1B,
Нехай ABCD – осьовий переріз конуса. BD і AC – діагоналі.
BD + AC; O – точка перетину діагоналей конуса.
Нехай OB = OC = x, AO = OD = y.
ΔBOC – прямокутний. OB2 + OC2 = BC2; BC2 = 2×2,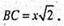 
ΔAOD – прямокутний. AO = OD = у, AO2 + OD2= AD2.
AD2= у2 + у2; AD2 = 2у2;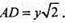 
Проведемо BE + AD; CK + AD;
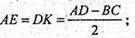
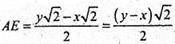
Або з ΔABE: AE = AB × cos α = I × cos α.
Отже: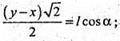 
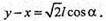
Із ΔABE: BE = AB × sin α; BE = l × sin α.
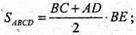
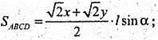
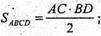
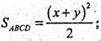
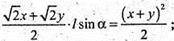
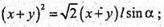
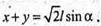
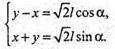
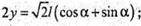
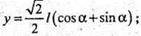
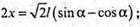
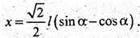
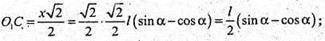
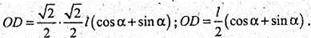
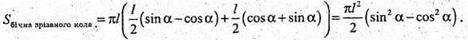
Відповідь: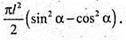 
1009.
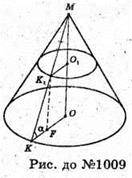
Нехай дано зрізаний конус. Площа нижньої основи конуса – S1.
Площа верхньої основи конуса – S2.
S3- площа бічної поверхні конуса.
S1 : S2 : S3 = а : b : с.
Нехай K1K – твірна конуса. ∠K1KO = α,
K1KO – кут між твірною конуса та площею його нижньої основи.
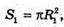де R1 =KO; 
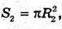де R2 = K1O1;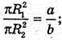 
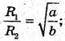
Sбічна конуса = π(R1 +R2) ×l, де l = K1K,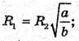 
KF = ОK.
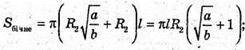
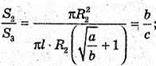
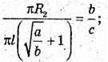
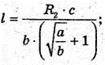
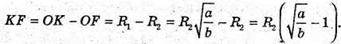
ΔKK1F – прямокутний.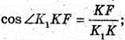 
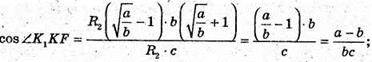
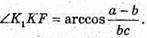
Відповідь: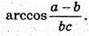 
1010.
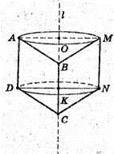
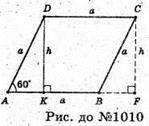
Нехай ромб ABCD обертається навколо прямої І, що містить його сторону.
AB = BC = CD = AD = a. ∠DAB = 60°. AO і DK – висоти ромба. DK + АВ.
З ΔADK: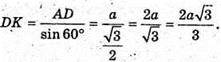 
CF + AB. ΔADK = ΔЕСВ. BF = AK.
S поверхні = S б. цил. ADNM – S б. к. ABM + S б. к. DCN. S б. к. ABM = б. к. DCN
Oтже, S поверхні =S б. цил. ADNM – S б. цил. = 2πR× L. де R = DK, L = AD.
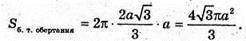
Відповідь: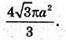 
1011.
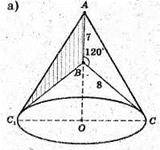
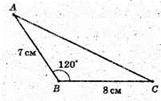
А) Нехай дано Δ ABC. AB = 7 см, BC – 8 см. AB найменша сторона ΔABC.
Δ ABC. За теоремою косинусів маємо: AC2 = AB2 + BC2- 2AB × BC × cos 120°.
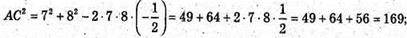
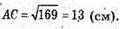
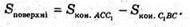
OC – висота Δ АВС, проведена до сторони АВ.
ΔOBC – прямокутний.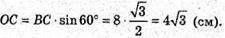 
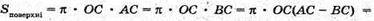
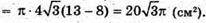
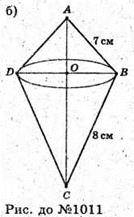
Б) Нехай дано ΔABC. AB = 7 см, BC = 8 см, AC = 13 см.
Нехай ΔABC обертається, навколо найбільшої сторони AC = 13 см.
S поверхне обертання = S б. к. ABD = S б. к. CBD.
OB – висота AABC, проведена до сторони АС.
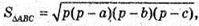
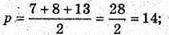
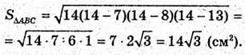
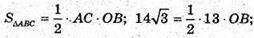
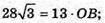
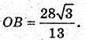
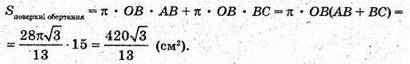
Відповідь: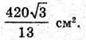 
1012.
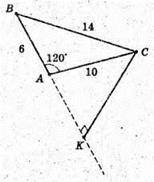
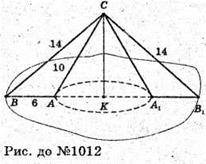
Нехай дано ΔАВС, AB = 6 см, AC = 10 см, ∠BAC = 120°.
∠C – найменший кут трикутника ABC. CK + AB,
CK – висота ΔABC, проведена до найменшої сторони.
S поверхні обертання = S бічна конуса BCB1 = S бічна конуса ACA1
S к. BCB1 = π × BK × BC + π × AK × АС.
ΔАВС: за теоремою BC2 = AB2 + AC2- 2АВ × AC × cos 120°;
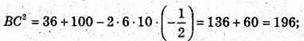
BC = 14 (см).
ΔСАК – прямокутний. ∠CAK = 60°.
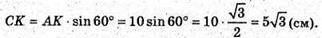
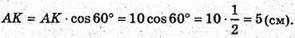
S бічна = π × 11 × 14 + π × 5 × 10 = 154π + 50π = 204π (см 2).
Відповідь: 204π см2.
1013.
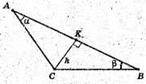
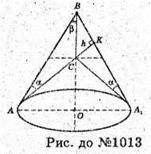
Нехай дано тупокутний ΔАВС, ∠A = α, ∠B = β.
BC – сторона, що лежить проти кута α.
∠C = 180° – (а + β), h – найменша висота, проведена до найбільшої сторони. Найбільша сторона ΔABC, сторона AB, що лежить навпроти тупого кута С.
CK + AS, CK = h.
S тіла обертання = S б. кон. ABA1 + S б. кон. ACA1
S поверхні = π × AO × AB + π × AO × AC = π × AO(AB + АС).
ΔACK – прямокутний.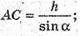 
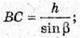
AB = AK + BK = h ctg α + h ctg β = h(ctg α + ctg β). ΔAOC – прямокутний.
∠CAO = 90° – α.
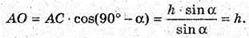
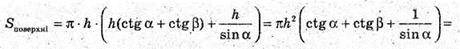
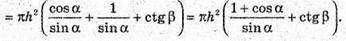
Відповідь: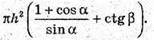 
1014.
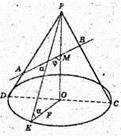
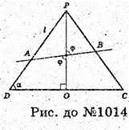
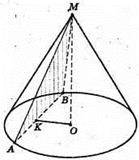
Через середину висоти конуса проведено пряму, якa утворює з висотою кут φ і перетинає бічну поверхню конуса в точках А і В. DP = l. PK – твірна конуса, ∠PKO = α. α – кут нахилу твірної до площини основи.
PO = l × sin α; DO = l × cos α. PO = PM + MO; AB= AM + MB,
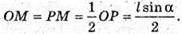∠OPC = ∠DPO = 90° – α.
ΔOPB. За теоремою синусів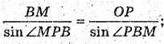 
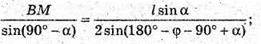
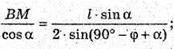
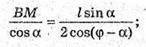
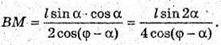
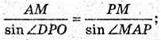
ΔАМР: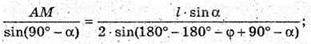 
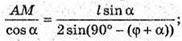
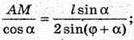
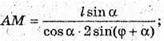
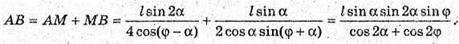
Відповідь: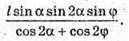 
1015.
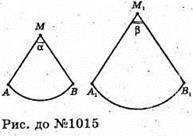
Нехай через вершину конуса проведено площину МАВ, яка ділить його бічну поверхню на дві частини. Розгорнули ці частини на площину і дістали 2 сектори з кутами α і β. MA = MA1 = I = Rсект.
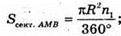
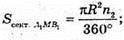
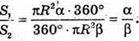
Довжина дуги кола І сектора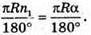 
Довжина дуги кола II сектора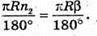 
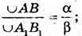AM – твірна конуса.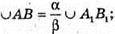 
C = 2π × R1, C – довжина кола, R1- радіус основи кола.
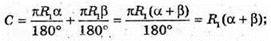
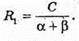
∠AMB – кут при вершині у проведеному перерізі.
(1 votes, average: 5.00 out of 5)
Loading...