Головна ⇒ 📌ГДЗ з математики ⇒ Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих

Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих

Розділ 2. Взаємне розміщення прямих па площині

§ 9. Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих

170. Рис. 119: ∠1 і ∠2 – внутрішні різносторонні кути.

Рис. 120: ∠1 і ∠2 – відповідні кути.

Рис,121: ∠1 i ∠2 – внутрішні різносторонні кути.

171. Внутрішні односторонні кути: ∠ANM і ∠NMB, ∠CNM і ∠NMD.

Внутрішні різносторонні кути: ∠ANM і ∠NMD, ∠CNM і ∠NMB.

Відповідні кути: ∠AKN і ∠NMB, ∠CKN і ∠NMD, ∠CNM і ∠DML, ∠ANM i ∠BML.

172. Внутрішні односторонні кути: ∠FCM та ∠CML, ∠PCM та ∠CMD.

Внутрішні

різносторонні кути: ∠FCM та ∠CMD, ∠PCM та ∠CML.

Відповідні кути: ∠BCF та ∠CML, ∠FCM та ∠LMK, ∠BCP та ∠CMD, ∠PCM та ∠DMK.

174. Рис. 125: а || b (згідно з наслідком 1, оскільки внутрішні різносторонні кути рівні).

Рис. 126: прямі а і b перетинаються (згідно з наслідком 2, оскільки сума внутрішніх односторонніх кутів не дорівнює 180°).

Рис. 127: а || b (згідно з ознакою паралельності прямих, оскільки відповідні кути рівні).

Рис. 128: а і b перетинаються, бо внутрішні різносторонні кути не рівні.

Рис. 129: а || b, оскільки сума внутрішніх односторонніх кутів дорівнює 180° (наслідок 2).

Рис. 130: а і b перетинаються, бо відповідні

кути не рівні.

175.

Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих

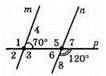
Позначимо кути цифрами від 1 до 8.

∠2 = 70° (як вертикальний кут до ∠4).

∠1 = 180° – 70° = 110° (як суміжний кут до ∠4).

∠3 = 110° (як вертикальний до ∠1).

∠5 = 120° (як вертикальний кут до ∠8).

∠6 = 180° – 120° = 60° (як суміжний кут до ∠8).

∠7 = ∠6 = 60° (як вертикальний до ∠6).

Прямі m і n перетинаються.

176.

Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих

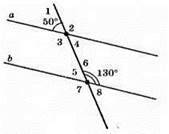
Позначимо кути цифрами від 1 до 8.

∠4 = ∠1 = 50° (як вертикальний кут до ∠1).

∠2 = 180° – 50° = 130° (як суміжний з ∠1).

∠3 = ∠2 = 130° (як вертикальний до ∠2).

∠7 = ∠6 = 130° (як вертикальний до ∠6).

∠5 = 180° – 130° = 50° (як суміжний з ∠6).

∠5 = ∠8 = 50° (як вертикальний до ∠3).

А || b, оскільки ∠2 = ∠6 = 130° (відповідні кути).

Відповідь: а || b.

177.

Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих

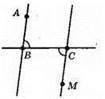
∠ABC і ∠BCM – внутрішні різносторонні кути для прямих AB і CM і січної ВC. Точки А і М розміщені по різні боки від ВС.

178.

Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих

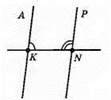
∠AKN і ∠KNP – внутрішні односторонні кути для прямих AK і PN і січної KN.

179. На рисунку 135 а || b, оскільки сума внутрішніх односторонніх кутів ∠1 та ∠2 дорівнює 180°.

180. На рисунку 135 b || с, оскільки відповідні кути рівні (∠2 = ∠3 = 60°).

181.

Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих

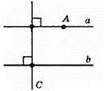
Проведемо через спільну сторону косинців пряму с.

С ⊥ а, с ⊥ b. Отже, прямі а і b перпендикулярні до однієї прямої.

За наслідком 3 (дві прямі, перпендикулярні до третьої прямої, паралельні) пряма а || b.

182.

Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих

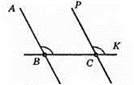
1) ∠ABC= 115°.

2) За допомогою транспортира будуємо кут ∠PCK = 115°.

3) AB || PC, оскільки відповідні кути ∠ABC і ∠PCK рівні (згідно з ознакою паралельності прямих).

183.

Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих

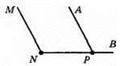
1) ∠MNP = 125°.

2) За допомогою транспортира будуємо ∠APB = 125°.

3) MN || АР, оскільки відповідні кути ∠MNP і ∠APB рівні (згідно з ознакою Паралельності прямих).

184.

Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих

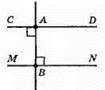
Оскільки прямі CD і MN перпендикулярні до однієї прямої AB, то за наслідком 3 – CD || MN.

185.

Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих

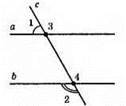
Доведення. ∠1 і ∠3 – суміжні. За властивістю суміжних кутів ∠1 + ∠3 = 180°. Звідси ∠3 = 180° – ∠1. За умовою ∠1 + ∠2 = 180°, тоді ∠2 = 180° – ∠1. ∠4 = ∠2, як вертикальні кути, отже, ∠4 = 180° – ∠1. Звідси маємо ∠3 = ∠4. Оскільки ∠3 і ∠4 Відповідні і рівні, то а || b.

186.

Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих

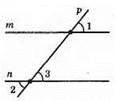
Доведення. ∠2 i ∠3 – вертикальні, ∠2 = ∠3. За умовою ∠1 = ∠2. Звідси ∠3 = ∠1. Оскільки ці кути відповідні і рівні, то m || n.

187.

Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих

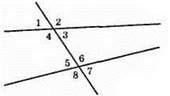
∠4 + ∠5 = 190°.

1) ∠2 = ∠4 (як вертикальні кути), ∠7 = ∠5 (як вертикальні кути). Отже, ∠2 + ∠7 = ∠4 + ∠5 = 190°.

2) ∠1 + ∠4 = 180° (як суміжні кути). Звідси ∠1 = 180° – ∠4.

∠5 + ∠8 = 180° (як суміжні кути). Звідси ∠8 = 180° – ∠5.

Отже, ∠1 + ∠8 = 180° – ∠4 + 180° – ∠5 = 360° = (∠4 + ∠5) = 360° – 190° = 170°.

3) ∠5 + ∠6 = 180° (як суміжні кути). Звідси ∠6 = 180° – ∠5.

∠3 + ∠4 = 180° (як суміжні кути). Звідси ∠3 = 180° – ∠4.

Отже, ∠3 + ∠6 = 180° – ∠4 + 180° – ∠5 = 360° – (∠4 + ∠5) – 360° – 190° = 170°.

Відповідь: 1) 190°; 2) 170°; 3) 170°.

188. ∠3 + ∠6 = 160°.

1) ∠2 + ∠3 = 180° (як суміжні кути). Звідси ∠2 = 180° – ∠3.

∠6 + ∠7 = 180° (як суміжні кути). Звідси ∠7 = 180° – ∠6.

Отже, ∠2 + ∠7 = 180° – ∠3 + 180° – ∠6 = 360°-160° = 200°.

2) ∠1 = ∠3 (як вертикальні кути). ∠8 = ∠6 (як вертикальні кути).

Отже, ∠1 + ∠8 = ∠3 + ∠6 = 160°.

3) ∠4 + ∠3 = 180° (як суміжні кути). Звідси ∠4 = 180° – ∠3.

∠5 + ∠6 = 180° (як суміжні кут). Звідси ∠5 = 180° = ∠6.

Отже, ∠4 + ∠5 = 180° – ∠3 + 180° – ∠6 = 360° – (∠3 + ∠6) = 360° – 160° = 200°.

Відповідь: 1) 200°; 2) 160°; 3) 200°.

189.

Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих

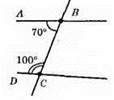
∠ABC i ∠BCD – внутрішні односторонні кути. ∠ABC + ∠BCD = 70° + 100° = 170°. Прямі AB і CD не можуть бути паралельні, оскільки у паралельних прямих сума внутрішніх односторонніх кутів дорівнює 180° (наслідок 2).

190.

Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих

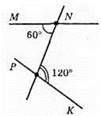
∠MNP і ∠NРК – внутрішні різносторонні кути. Якби прямі MN і РК були паралельні, то кути MNP і NPK були б рівні. Але ∠MNP = 60°, ∠NPK = 120°. Отже, MN і РК не паралельні.

191.

Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих

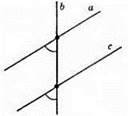
Прямі а і с паралельні, оскільки відповідні кути при перетині прямих а і с прямою b, рівні.

192.

Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих

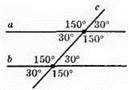
Так, прямі а і b паралельні.

193.

Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих

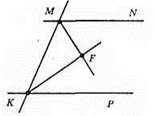
Доведення. ∠NMK і ∠MKP – внутрішні односторонні кути. Знайдемо їх суму. MF – бісектриса кута NMK, ∠NMK = 2∠FMK.

KF – бісектриса кута МКР, ∠MKP = 2∠MKF.

За умовою ∠MKF + ∠FMK = 90°. Знайдемо суму кутів ∠NMK і ∠MKP.

∠NMK + ∠MKP = 2∠FMK + 2∠MKF = 2(∠FMK + ∠MKF) = 2 x 90° = 180°. Оскільки сума внутрішніх односторонніх кутів дорівнює 180°, то MN || KP.

194.

Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих

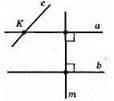
Оскільки прямі а і b перпендикулярні до прямої m, то за наслідком 3 вони паралельні між собою, а || b. Позначимо К – точку перетину прямих а і с. Припустимо, що прямі b і с не перетинаються. Тоді через т. К проходять дві різні прямі а і с, що паралельні прямій b, що суперечить аксіомі про паралельність прямих. Отже, прямі с і b перетинаються.

195.

Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих

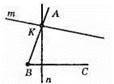
1) ∠ABC = 70°.

2) m ⊥ ВА, n ⊥ ВС.

3) Кут між прямими m і n дорівнює 70°.

196.

Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих

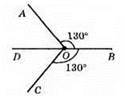
∠AOB = ∠BOC = 130°. ∠AOC = ∠AOD + ∠DOC, ∠AOD + ∠AOB = 180° (як суміжні кути). Звідси ∠AOD = 180° – 130° = 50°. ∠DOC + ∠BOC = 180° (як вертикальні кути). ∠DOC = 180° – 130° = 50°.

∠AOC = 50° + 50° = 100°.

Відповідь: 100°.

197. Так, можна. Наприклад так.

Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною Розділ 2. Взаємне розміщення прямих па площині § 10. Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною 199. 1) ∠1 = ∠8, ∠6 = ∠3 (як відповідні кути при паралельних прямих а і b і січній с). 2) ∠2 = ∠4 (як внутрішні різносторонні кути при паралельних прямих а і b і […]...

  2. Ознаки паралельності двох прямих § 3. Паралельні прямі. Сума кутів трикутника 13. Ознаки паралельності двох прямих Практичні завдання 300. 1) Кути АОМ і CEO – відповідні; 2) кути АОЕ і СЕК – відповідні; 3) кути АОE і OED – різносторонні; 4) кути АОЕ і CEO – односторонні. 1) відповідні; 2) односторонні; 3) різносторонні. 301. 1) ∠1 i ∠5; ∠2 […]...

  3. ОЗНАКИ ПАРАЛЕЛЬНОСТІ ПРЯМИХ РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ & 6. ОЗНАКИ ПАРАЛЕЛЬНОСТІ ПРЯМИХ Важливу роль у дослідженні паралельності прямих відіграють поняття січної та деяких пар кутів. Нехай а і b – дві довільні прямі площини. Пряму с, що їх перетинає, називають січною прямих а і b (мал. 73). Прямі а і b з їх січною с […]...

  4. Властивості кутів, утворених при перетині двох паралельних прямих січною Урок № 32 Тема. Властивості кутів, утворених при перетині двох паралельних прямих січною Мета: закріпити знання учнів про зміст та схему доведення теореми про властивості кутів та наслідків з неї; сформувати уявлення учнів про відстань між двома паралельними прямими; сформувати вміння використовувати названі вище теоретичні відомості під час розв’язування задач на знаходження кутів при паралельних […]...

  5. Ознаки паралельності прямих Урок № 30 Тема. Ознаки паралельності прямих Мета: закріпити знання учнів про ознаки паралельності двох прямих (за кутами, що утворилися при перетині даних прямих січною). Сформувати вміння: – визначати вид двох кутів, що утворилися при перетині двох прямих січною; – за певним співвідношенням цих кутів робити висновок щодо паралельності прямих; – для встановлення співвідношення кутів […]...

  6. Кути – ПЛАНІМЕТРІЯ Формули й таблиці МАТЕМАТИКА ПЛАНІМЕТРІЯ Паралельні прямі перетинають сторони кута. Кути Кут – плоска фігура, що складається із двох променів зі цільним початком й обмеженої ними частини площини. Промені називаються сторонами, їхня спільна точка – вершиною, обмежена ними частина площини – внутрішньою областю. α + α’ = 180° α і α’ – суміжні кути β […]...

  7. Вертикальні кути. Кут між двома прямими, що перетинаються Розділ 2. Взаємне розміщення прямих па площині § 6. Вертикальні кути. Кут між двома прямими, що перетинаються 107. 1) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 15°, дорівнює 15°. 2) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 129°, дорівнює 129°. Відповідь: 1) 15°; […]...

  8. Вправи 375-424 375. ВС – бісектриса ∠ABD; ∠ABD = 80° + 80° = 160°; ∠BAC + ∠ABD = 20° + 160° = 180°; ∠BAC і ∠ABD – внутрішні односторонні кути при прямих АС і BD та січній АВ. Отже, BD || АС. 376. ∠A = 70°, ∠B = 40°, BE – бісектриса ∠ABD; ∠DBE = ∠ABE = […]...

  9. Вправи для повторення до розділу 2 Розділ 2. Взаємне розміщення прямих па площині Вправи для повторення до розділу 2 До § 5. 226. На рис. 184 суміжні кути ∠2 і ∠3. на рис. 185 суміжні кути ∠1 і ∠4 та ∠2 i ∠3. На рис. 186 суміжні кути ∠1 і ∠2 та ∠3 i ∠4. 227. 1) Так, можна. Треба побудувати […]...

  10. Вертикальні кути Розділ 1. Найпростіші геометричні фігури та їх властивості § 5. Вертикальні кути 152. 1) ∠AYX і ∠BYZ – вертикальні; 2) ∠OLK і ∠MLN – не вертикальні. 153. 1) ∠AOD – вертикальний з кутом 1; 2) ∠АОС і ∠DOB – суміжні з кутом 1. 154. ∠BOA і ∠COD – суміжні. ∠BOA = ∠COD = 60°. 155. […]...

  11. Суміжні та вертикальні кути § 1. Найпростіші геометричні фігури та їхні властивості § 4. Суміжні та вертикальні кути Практичні завдання 86. ∠BAC – гострий, ∠OAB – суміжний до кута ВАС. ∠АОВ – прямий, ∠COA – суміжний до кута АОВ. ∠BOC – тупий, ∠AOB – суміжний до кута ВОС. 87. ∠AOC і ∠COB – суміжні. 88. а) ∠ABD i ∠CBD; […]...

  12. Вправи 325-374 325. ?ABC; AB = AC; ?A1B1C1; A1B1 = A1C1; ∠B = ∠B1; BK = B1K1. ∠AKB = ∠CKB = ∠A1K1B1 = ∠C1K1B1 = 90°. ?АВK = ?A1B1K1. 1) BK = В1K1; 2) ∠1 = ∠2; 3) ∠3 = ∠4, отже, AB =A1B1. ?АВС = ?А1В1С1. AB = A1B1; BC = В1С1; ∠B = ∠B1. 326. […]...

  13. Перша та друга ознаки рівності трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 13. Перша та друга ознаки рівності трикутників 301. На рис. 227 трикутники рівні за першою ознакою (за двома сторонами і кутом між ними). На рис. 228 трикутники рівні за другою ознакою (за стороною і прилеглими двома кутами). 302. У? ABC і? CDA спільний елемент – сторона AВ. У? […]...

  14. Ознаки паралельності прямих. Сума кутів трикутника Урок № 40 Тема. Ознаки паралельності прямих. Сума кутів трикутника Мета: перевірити рівень засвоєння знань та вмінь, передбачених програмою, із зазначених тем. Тип уроку: контроль та корекція знань. ХІД УРОКУ I. Організаційний момент II. Перевірка домашнього завдання Зібрати зошити з виконаною домашньою контрольною роботою. Роботу оцінити та врахувати в тематичному балі. III. Умова контрольної роботи […]...

  15. Паралельні прямі Геометрія Основні властивості найпростіших геометричних фігур Паралельні прямі На рисунку зображені кути, утворені в результаті перетину двох прямих січною: і ; і – внутрішні різносторонні кути при прямих a, b і січній c. і ; і – внутрішні односторонні. і ; і – зовнішні односторонні. і ; і – зовнішні різносторонні. і ; і ; […]...

  16. Ознака паралельності прямих Урок 9 Тема. Ознака паралельності прямих Мета уроку: вивчення ознаки паралельності прямих, формування умінь застосовувати ознаку паралельності до розв’язування задач. Обладнання: моделі прямокутного паралелепіпеда і куба. Хід уроку І. Перевірка домашнього завдання 1. Два учні відтворюють розв’язання задач № 5 (1, 3) та 7 (1, 3). 2. Проведення тесту на визначення істинності математичних тверджень. Тест […]...

  17. Суміжні й вертикальні кути Геометрія Основні властивості найпростіших геометричних фігур Суміжні й вертикальні кути Два кути називаються Суміжними, якщо в них одна сторона спільна, а інші сторони є доповняльними півпрямими. На рисунку і – суміжні. Властивості суміжних кутів Теорема 1. Сума суміжних кутів дорівнює . (Зверніть увагу: кути, сума яких дорівнює , не обов’язково суміжні.) Теорема 2. Коли два […]...

  18. Ознака паралельності прямих Геометрія Стереометрія Ознака паралельності прямих Теорема. Дві прямі, паралельні третій прямій, паралельні між собою. Із цієї теореми випливає, що середини сторін просторового чотирикутника (див. рисунок) є вершинами паралелограма (вершини просторового чотирикутника не лежать в одній площині). Зверніть увагу: якщо ABCD – просторовий чотирикутник, то його діагоналі AC і BD – мимобіжні прямі....

  19. СУМІЖНІ І ВЕРТИКАЛЬНІ КУТИ Геометрія Евкліда є лише першим кроком до вивчення форм реального простору. О. Смогоржевський РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ У цьому розділі підручника ви розширите і поглибите свої знання про прямі і промені однієї площини, ознайомитеся з дуже важливими поняттями: суміжні кути, вертикальні кути, перпендикулярні прямі, паралельні прямі тощо, а також із важливими загальноматематичними […]...

  20. Взаємне розміщення двох прямих у просторі Урок 7 Тема. Взаємне розміщення двох прямих у просторі Мета уроку: вивчення взаємного розташування двох прямих у просторі: прямі, що перетинаються; паралельні прямі; мимобіжні прямі. Формування понять: паралельні прямі, мимобіжні прямі. Обладнання: стереометричний набір, каркасна модель куба, схема “Взаємне розміщення двох прямих у просторі”. Перевірку правильності виконання домашньої задачі провести шляхом фронтальної бесіди за записами, […]...

  21. ВЛАСТИВОСТІ ПАРАЛЕЛЬНИХ ПРЯМИХ РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ & 7. ВЛАСТИВОСТІ ПАРАЛЕЛЬНИХ ПРЯМИХ ЗАДАЧА Дано пряму а і точку Р, що не належить цій прямій. Проведіть через точку Р пряму, паралельну прямій а. – За допомогою лінійки і косинця побудову можна виконати, як показано на малюнку 90. Чи можна через точку Р провести дві різні прямі, […]...

  22. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої Розділ 2. Взаємне розміщення прямих па площині § 7. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої 128. m ⊥ n, MN ⊥ АВ. 129. KA ⊥ c, ВМ ⊥ с. 130. ВL ⊥ a. MВ ⊥ a. 131. 1) Відрізки AB і MN перпендикулярні, оскільки вони лежать на перпендикулярних прямих a і b. 2) […]...

  23. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 19. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників 466. 1) PF – гіпотенуза, PL і LF – катети. 2) PF довша за PL, PF довша за LF, оскільки PF – гіпотенуза. 467. На рис. 321 трикутники рівні за двома катетами. Оскільки АС = ML, СВ = LP, […]...

  24. Пряма й обернена теореми Геометрія Основні властивості найпростіших геометричних фігур Пряма й обернена теореми Формулювання теореми складається з двох частин. В одній говориться про те, що дано. Ця частина називається Умовою. У другій частині говориться про те, що треба довести. Ця частина називається Висновком. Приклади 1) Якщо кути суміжні, то їх сума дорівнює 180°. Умова Висновок 2) У прямокутному […]...

  25. Вправи 100-49 100. А || b, с || d. 4 точки перетину. 101. 1) Всі чотири прямі перетинають пряму с. 2) Одна пряма паралельна, три перетинають пряму с. 102. 1) m || с; 2) m || b; в) m || а. 103. а || b. Якщо b i c не перетинаються, то через т. М проведено 2 […]...

  26. Властивості й ознака рівнобедреного трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 12. Властивості й ознака рівнобедреного трикутника 476. На мал. 72: ML і МК – бічні сторони, KL – основа, ∠K = ∠L. 477. KD = DF, КЕ = EF, ∠K = ∠F, ∠KDE = ∠FDE, ∠DEK = ∠DEF = 90°. 478. Щоб провести бісектрису, медіану і […]...

  27. Многогранні кути 607. Правильний октаедр має 8 граней, кожна з яких – правильний трикутник. Він має 6 чотиригранних кутів. 608. Чотиригранний кут 40°; 70°; 110° і 140° існує неопуклий. 609. Якщо всі плоскі кути чотиригранного кута рівні, то кожний його двогранний кут дорівнює протилежному (октаедр). Площини, які проходять через його протилежні ребра, – перпендикулярні. 611. Якщо у […]...

  28. Властивості кутів трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 10. Властивості кутів трикутника 344. ∠E = 60°, ∠F = 40°, ∠D = 80°. ∠E + ∠F + ∠D = 60° + 40° + 80° = 180°. 345. На мал. 208 неправильно сказано градусну міру кутів? АВС, оскільки? ABC – прямокутний, a ∠B + ∠C = […]...

  29. Вправи 150-175 150. ∠1 = 90°, ∠2 = ∠1 = 90° – вертикальні кути; ∠3 – суміжний куту ∠1. ∠3 = 180° – 90° = 90°, ∠3 = ∠4 = 90° (вертикальні кути). 151. ∠(ac) = 70°; ∠(ab) = 90°; ∠(bc) = 90° – ∠(ac) = 90° – 70° = 20°. 152. а ⊥ с; ∠(ab) = […]...

  30. Розміщення двох площин у просторі. Паралельні площини. Ознака паралельності площин Урок 15 Тема. Розміщення двох площин у просторі. Паралельні площини. Ознака паралельності площин Мета уроку: формування знань учнів про взаємне розміщення двох площин у просторі. Вивчення ознаки паралельності двох площин. Обладнання: стереометричний набір, схема “Взаємне розміщення двох площин”. Хід уроку 1. Перевірити наявність виконаних завдань та відповісти на запитан­ня, які виникли в учнів під час […]...

  31. Вертикальні кути. Кут між прямими Урок № 11 Тема. Вертикальні кути. Кут між прямими Мета: домогтися засвоєння учнями означення вертикальних кутів, формулювання і доведення теореми про властивість вертикальних кутів; означення кутів між прямими. Сформувати вміння: – будувати вертикальні кути; – знаходити вертикальні кути на рисунку; – розв’язувати задачі із застосуванням теореми про рівність вертикальних кутів та суму суміжних кутів. Тип […]...

  32. Властивості прямокутного трикутника § 3. Паралельні прямі. Сума кутів трикутника § 17. Властивості прямокутного трикутника 457. Найбільший катет трикутника дорівнює 24 см. 458. ?DEF – прямокутний, ∠F = 90°, ∠D = 30°, DE = 18 см. Відповідь: 9 см. 459. ?KCM – прямокутний, ∠M = 90°, ∠C = 60°, MC = 7 см. ∠MKC = 90° – 60° […]...

  33. Суміжні кути Урок № 10 Тема. Суміжні кути Мета: домогтися розуміння учнями змісту наслідків з теореми про суму суміжних кутів та змісту понять “наслідок”, “посилання”; використовуючи знання теореми про суміжні кути та її наслідки, виробити вміння розв’язувати задачі на обчислення та доведення, в яких йдеться про суміжні кути. Тип уроку: застосування знань, умінь та навичок. Наочність і […]...

  34. Рівність геометричних фігур Розділ 1. Найпростіші геометричні фігури та їх властивості § 11. Рівність геометричних фігур 397. Щоб сумістити фігури F1 i F, можна скопіювати фігуру F1 на кальку, потім перевернути кальку і покласти на фігуру F. 398. Відрізки OP і MN сумістити не можна, бо вони мають різну довжину. 399. Кути ABC і MON сумістити не можна, […]...

  35. Зовнішній кут трикутника та його властивості Розділ 3. Трикутники. Ознаки рівності трикутників § 18. Зовнішній кут трикутника та його властивості 438. ∠BAK – зовнішній кут при вершині А. 439. ∠LDP – зовнішній кут при вершині D. 441. ∠A + ∠B = 70° – за властивістю зовнішнього кута трикутника. 442. Зовнішній кут трикутника при вершині С дорівнює 74° згідно з властивістю зовнішнього […]...

  36. Паралельність прямих і площини Геометрія Стереометрія Паралельність прямих і площини Дві прямі в просторі називаються Паралельними, якщо вони лежать в одній площині й не перетинаються. Прямі, які не лежать в одній площині, називаються Мимобіж­ними. Зверніть увагу: “не лежать в одній площині” і “лежать у різних площинах” – це різні твердження. Наприклад, паралельні прямі a і b лежать у різних […]...

  37. Сума кутів трикутника. Нерівність трикутника § 3. Паралельні прямі. Сума кутів трикутника § 15. Сума кутів трикутника. Нерівність трикутника Вправи 357. Нехай х° – третій кут трикутника, тоді 35 + 96 + х = 180, звідси х + 131 = 180; х = 180 – 131; х = 49. Отже, третій кут дорівнює 49°. Відповідь: 49°. 358. Нехай х° – […]...

  38. Ознака мимобіжності прямих Урок 10 Тема. Ознака мимобіжності прямих Мета уроку: вивчення ознаки мимобіжності прямих, формування вмінь застосовувати ознаку мимобіжності двох прямих до розв’язування задач. Обладнання: стереометричний набір, моделі тетраедра і куба. 1. Перевірити наявність виконаних завдань та відповісти на запитан­ня, які виникли в учнів під час виконання цих завдань. 2. Самостійна робота. 1) Трикутник АВС і паралелограм […]...

  39. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника Розділ 3. Трикутники. Ознаки рівності трикутників § 15. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника 351. 1) AT – висота трикутника ABC. 2) AN – медіана трикутника ABC. 3) АР – бісектриса трикутника? AВС. 352. Оскільки AK – висота, то ∠BKA = ∠CKA = 90°. 353. Оскільки АК – бісектриса, то ∠BAK = […]...

  40. Описане та вписане коло трикутника § 3. Паралельні прямі. Сума кутів трикутника § 20. Описане та вписане коло трикутника 540. 1) Різносторонній гострокутний трикутник. 2) Прямокутний трикутник. 3) Тупокутний трикутник. 541. 1) Рівнобедрений гострокутний трикутник. 2) Рівнобедрений тупокутний трикутник. 542. 543. 544. Вправи 545. Медіана BD рівнобедреного трикутника ABC є в той же час і серединним перпендикуляром до сторони АС […]...

Ви зараз читаєте: Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих
«
»