Головна ⇒ 📌Формули й таблиці ⇒ Квадрат – ЧОТИРИКУТНИКИ
Квадрат – ЧОТИРИКУТНИКИ
Формули й таблиці
МАТЕМАТИКА
ЧОТИРИКУТНИКИ
Квадрат
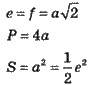
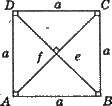
Діагоналі взаємноперпендикулярні, рівні і в точці перетину діляться навпіл. Всі внутрішні кути прямі. Всі сторони рівні.
Related posts:
- Ромб – ЧОТИРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ЧОТИРИКУТНИКИ Ромб Діагоналі взаємноперпендикулярні і в точці перетину діляться навпіл. Всі сторони рівні. Протилежні сторони паралельні. Протилежні кути рівні....
- Прямокутник – ЧОТИРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ЧОТИРИКУТНИКИ Прямокутник Діагоналі рівні і точкою перетину діляться навпіл. Протилежні сторони рівні і паралельні. Всі кути прямі....
- Паралелограм – ЧОТИРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ЧОТИРИКУТНИКИ Паралелограм Діагоналі у точці перетину діляться навпіл. Протилежні кути рівні. Протилежні сторони рівні і паралельні....
- Квадрат Геометрія Чотирикутники Квадрат Квадрат – це прямокутник, у якого всі сторони рівні. Властивості квадрата Оскільки квадрат є паралелограмом, прямокутником і ромбом водночас, маємо: 1) у квадрата всі сторони рівні; 2) у квадрата всі кути рівні; 3) діагоналі квадрата рівні, перетинаються під прямим кутом, діляться в точці перетину навпіл, є бісектрисами його кутів; 4) діагоналі квадрата […]...
- Трапеція – ЧОТИРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ЧОТИРИКУТНИКИ Трапеція Щонайменше дві сторони паралельні, а дві інші – непаралельні Середня лінія трапеції – відрізок, що сполучає бічні сторони трапеції....
- Вписаний чотирикутник – ЧОТИРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ЧОТИРИКУТНИКИ Вписаний чотирикутник Усі вершини лежать на колі. Сума протилежних кутів дорівнює 180°....
- Вписані чотирикутники. Описані чотирикутники Урок № 22 Тема. Вписані чотирикутники. Описані чотирикутники Мета: працювати над засвоєнням учнями змісту понять: чотирикутник, вписаний у коло; чотирикутник, описаний навколо кола; розглянути зміст теорем про вписаний та описаний чотирикутники та схеми їх доведення. Сформувати вміння: – відтворювати вивчені твердження; – виконувати рисунок за описом; – використовувати вивчені теореми під час розв’язування теореми на […]...
- Ромб. Квадрат Урок № 9 Тема. Ромб. Квадрат Мета: працювати над засвоєнням учнями змісту означень, властивостей та ознак ромба і квадрата. Формувати вміння: – відтворювати вивчені твердження; – застосовувати властивості, ознаки ромба і квадрата до розв’язування типових задач; – застосовувати властивості, ознаки ромба і квадрата разом із раніше вивченими твердженнями в темі “Чотирикутники” до розв’язування задач підвищеного […]...
- Вписаний та описаний чотирикутники – КОЛО Формули й таблиці МАТЕМАТИКА КОЛО Вписаний та описаний чотирикутники Якщо сума протилежних кутів чотирикутника дорівнює 180°, то навколо нього можна описати коло: A + C = 180°, B + D = 180°. Якщо суми протилежних сторін чотирикутника рівні, то в нього можна вписати коло: AB + CD = BC + AD...
- Кути – ПЛАНІМЕТРІЯ Формули й таблиці МАТЕМАТИКА ПЛАНІМЕТРІЯ Паралельні прямі перетинають сторони кута. Кути Кут – плоска фігура, що складається із двох променів зі цільним початком й обмеженої ними частини площини. Промені називаються сторонами, їхня спільна точка – вершиною, обмежена ними частина площини – внутрішньою областю. α + α’ = 180° α і α’ – суміжні кути β […]...
- Паралелограм Геометрія Чотирикутники Чотирикутником називається фігура, яка складається з чотирьох точок і чотирьох відрізків, що послідовно їх сполучають. При цьому жодні три з даних точок не повинні лежати на одній прямій, а відрізки, які їх сполучають, не повинні перетинатися. Дані точки називаються Вершинами чотирикутника, а відрізки, що їх сполучають,- Сторонами чотирикутника. Вершини чотирикутника називаються Сусідніми, якщо […]...
- Правильні багатокутники – КОЛО Формули й таблиці МАТЕМАТИКА КОЛО Правильні багатокутники N – число кутів; R1 – радіус описаного кола; R2 – радіус вписаного кола; α – центральний кут; β – внутрішній кут; γ – зовнішній кут; Правильним називається багатокутник, у якому всі сторони і всі внутрішні кути рівні між собою....
- Теореми про рівність і подібність трикутників – ТРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ТРИКУТНИКИ Трикутник – де багатокутник із трьома сторонами. Сторони трикутника позначаються малими буквами, що відповідають позначенню протилежних вершин. Якщо всі три кути гострі – трикутник гострокутний. Якщо один з кутів прямий – прямокутний; сторони, що утворюють прямий кут, називаються катетами (а і b), сторона проти прямого кута – гіпотенузою (с). Якщо […]...
- Прямокутник Геометрія Чотирикутники Прямокутник Прямокутник – це паралелограм, у якого всі кути прямі. Властивості прямокутника Оскільки прямокутник є паралелограмом, він має всі властивості паралелограма і ще деякі інші. Теорема. Діагоналі прямокутника рівні. На рисунку . . ; – рівнобедрені. Ознаки прямокутника Теорема 1. Якщо в чотирикутнику всі кути рівні, то він є прямокутником. Теорема 2. Якщо […]...
- Прямокутник. Квадрат Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 22. Прямокутник. Квадрат На рисунку 156 зображено чотирикутник, у якого всі кути прямі. Такий чотирикутник, як відомо з молодших класів, називається прямокутником. Протилежні сторони прямокутника рівні між собою, тобто АВ = DC і AD = ВС. Сторони прямокутника, які не є протилежними, […]...
- Чотирикутники Урок № 1 Тема. Чотирикутники Мета: сформувати уявлення про чотирикутник, його елементи: вершина, сторона, діагональ, сусідні сторони (вершини), протилежні сторони (вершини); ввести поняття периметра чотирикутника. Сформувати первинні вміння: – відтворювати означення чотирикутника, його елементів; – знаходити на рисунку зображення чотирикутника та його елементів; – виконувати рисунки за описом; – розв’язувати найпростіші задачі на обчислення із […]...
- Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих Розділ 2. Взаємне розміщення прямих па площині § 9. Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих 170. Рис. 119: ∠1 і ∠2 – внутрішні різносторонні кути. Рис. 120: ∠1 і ∠2 – відповідні кути. Рис,121: ∠1 i ∠2 – внутрішні різносторонні кути. 171. Внутрішні односторонні кути: ∠ANM і ∠NMB, ∠CNM і ∠NMD. […]...
- Опуклі чотирикутники. Сума кутів чотирикутника Урок № 2 Тема. Опуклі чотирикутники. Сума кутів чотирикутника Мета: сформувати уявлення про внутрішню область чотирикутника, поняття опуклого та неопуклого чотирикутників, кута опуклого чотирикутника, сусідніх та протилежних кутів опуклого чотирикутника. Сформувати первинні вміння: – відтворювати вивчені означення; – розрізняти на готових рисунках вивчені об’єкти; – зображувати вивчені об’єкти на рисунку. Сформувати усвідомлене розуміння змісту теореми […]...
- КВАДРАТ. ПЕРИМЕТР КВАДРАТА ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ. ЗАДАЧІ НА ДВІ ДІЇ. ВИРАЗИ З ДУЖКАМИ ВИРАЗИ З ДУЖКАМИ Урок 32. КВАДРАТ. ПЕРИМЕТР КВАДРАТА Мета: навчити учнів розрізняти квадрат за істотними ознаками; вчити обчислювати периметр квадрата; розвивати пізнавальну активність, уміння спостерігати і порівнювати, робити висновки, висловлювати власну думку; виховувати культуру розумової праці. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ […]...
- Трапеція Геометрія Чотирикутники Трапеція Трапецією називається чотирикутник, у якого тільки дві протилежні сторони паралельні. Ці сторони називаються Основами трапеції, а дві інші – Бічними сторонами. Трапеція, в якої бічні сторони рівні, називається Рівнобічною (див. рисунок нижче зліва). Якщо одна з бічних сторін трапеції перпендикулярна до основ, трапеція називається Прямокутною (рисунок нижче справа). Теорема 1. Кути трапеції, […]...
- Ромб Геометрія Чотирикутники Ромб Ромб – це паралелограм, у якого всі сторони рівні. Властивості ромба Оскільки ромб є паралелограмом, він має всі властивості паралелограма і деякі інші. Теорема 1. Діагоналі ромба перетинаються під прямим кутом. Діагоналі ромба є бісектрисами його кутів. На рисунку ABCD – ромб; ; ; ; ; . Теорема 2. Діагоналі ромба розбивають […]...
- Формули скороченого множення – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Формули скороченого множення (а + b)2 = а2 + 2аb + b2 (квадрат суми); (a – b)2 = а2 – 2ab + b2 (квадрат різниці); A2 – b2 = (a + b)(a – b) (різниця квадратів); (a + b)3 = а3 + 3а2b + 3ab2 + b3 (куб суми); […]...
- Прямокутна система координат 11. 12. Точки А(4; 4; 4), В(-4; 4; 4), С(-4;-4; 4), П(4; 4; -4), D(-4; 4; -4), E(4; -4; 4), F(4; -4; -4), M(-4; -4; -4) віддалені від кожної з координатних площин на 4. 13. 14. О – початок координат. ОВ > ОА, отже, ближче до початку координат лежить т. А. 15. 16. Оскільки КТ […]...
- Паралельні прямі Геометрія Основні властивості найпростіших геометричних фігур Паралельні прямі На рисунку зображені кути, утворені в результаті перетину двох прямих січною: і ; і – внутрішні різносторонні кути при прямих a, b і січній c. і ; і – внутрішні односторонні. і ; і – зовнішні односторонні. і ; і – зовнішні різносторонні. і ; і ; […]...
- Вектори у просторі 156. ABCDEF – правильний шестикутник. А) Б) В) Але 157. 158. А) Б) В) 159. 160. А) Б) В) 161. 162. А(х; у; z). Тому -5 – х = З, x = -8; 4 – у = 4, у = 0; 1 – z = 2, z = -1. Отже, А(-8; 0; -1). 163. С(-2; […]...
- Правила диференціювання – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Правила диференціювання Правило 1. Якщо функції у = f(x) і у = g(x) мають похідну в точці х, то і їх сума має похідну в точці х, до того ж похідна суми дорівнює сумі похідних: Правило 2. Якщо функція у = f(x) має похідну в точці х, то і […]...
- Квадрат суми та квадрат різниці двох виразів 567. (5а + 3)2 = 25а2 + 30а + 9. 568. Тотожності: 3) (12а – b)2= 144а2 – 24аb + b2. Рівняння коренів не має. 577. (a – b)2 = (b – a)2 – тотожність, бо (a – b)2 = a2 – 2ab + b2; (b – a)2 = b2 – 2ab + a2, a […]...
- Формули перетворення сум у добутки – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули перетворення сум у добутки Для будь-яких α і β...
- Формули перетворення добутків у суми – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули перетворення добутків у суми Для будь-яких α і β...
- КВАДРАТ ДВОЧЛЕНА РОЗДІЛ 3 МНОГОЧЛЕНИ &11. КВАДРАТ ДВОЧЛЕНА Ви вже знаєте, як додавати, віднімати і множити многочлени. Як і числа, многочлени можна підносити до степеня з натуральним показником. Для цього достатньо помножити многочлен на себе стільки разів, скільки показує число в показнику степеня. В окремих випадках піднесення до степеня дозволяє спрощувати дії з многочленами. Розглянемо їх. Запам’ятайте! […]...
« АТАВІЗМ