Лінійне рівняння з однією змінною
Урок № 11
Тема. Лінійне рівняння з однією змінною
Мета: перевірити рівень засвоєння знань, умінь та навичок, передбачених програмою, в ході вивчення названої теми.
Тип уроку: контроль знань.
Хід уроку
І. Умова тематичної контрольної роботи
Варіант 1 | Варіант 2 |
№ 1. Чи рівносильні рівняння? Чому? 3х + 4 = 7 та 2(х + 3) – 5 = x + 2. | № 1. Чи рівносильні рівняння? Чому? Х – 7 + 2 = 3х та х – 7 = 3(х – 1) + 1. |
№ 2. Розв’яжіть рівняння 0,2(7 – | № 2. Розв’яжіть рівняння 0,4(2x – 7) + 1,2(3x + 0,7) = 1,6x. |
№ 3. Розв’яжіть задачу, склавши рівняння. Перший автомобіль долає шлях між містами за 5 год. Другий автомобіль, швидкість якого на 20 км/год. більша, ніж першого, долає той самий шлях за 4 год. Знайдіть швидкість автомобілів. | № 3. Розв’яжіть задачу, склавши рівняння. Перший автомобіль долає шлях між двома містами за 1,5 і од, а другий – за 1,2 год. Швидкість другого автомобіля більша від швидкості першого на 15 км/юд Знайдіть відстань між милами. |
№ 4. Розв’яжіть рівняння
| № 4. Розв’яжіть рівняння
|
№ 5. Розв’яжіть задачу. У книжковій шафі було в 6 разів більше книжок, ніж на етажерці. Після того як із шафи взяли 46 книжок, а з етажерки 18, на етажерці залишилося на 97 книжок менше, ніж у шафі. Скільки книг було в шафі, а скільки на етажерці спочатку? | № 5. Розв’яжіть задачу. В автопарку було вантажівок у 5 разів більше, ніж легкових автомобілів. Після того як у рейс вийшло 58 вантажівок і 15 легкових авто, в автопарку залишилось вантажівок на 61 більше, ніж легкових авто. Скільки легкових авто і скільки вантажівок було в автопарку спочатку? |
№ 6. Розв’яжіть рівняння 5 |4 + 2(х – 3)| = 1. | № 6. Розв’яжіть рівняння 2(|х| – 3) = 4|х| – 10. |
№ 7*. При якому значенні а рівняння (2 + а)х = 10: 1) має корінь 5; 2) не має коренів? | № 7*. При якому значенні а рівняння (а – 3)х = 8: 1) має корінь 4; 2) не має коренів? |
II. Розв’язання та відповіді до тематичної контрольної роботи
Варіант 1
№ 1. 3х + 4 = 7; 3х = 3; х = 1; 2(х + 3) – 5 = х + 2; 2х + 1 = х + 2; х = 1.
Рівняння мають однакові корені.
Відповідь. Рівносильні, бо мають однакові корені.
№ 2. 0,2(7 – 2y) = 2,3 – 0,3(y – 6); 1,4 – 0,4y = 2,3 – 0,3y + 1,8;
1,4 – 0,4у = 4,1 – 0,3y; – 0,4y + 0,3у = 4,1 – 1,4; -0,1y = 2,7; у = 2,7 : (- 0,1);
У = -27. Відповідь. -27.
№ 3. | V (км/год.) | T (год.) | S (км) |
А1 | Х | 5 | 5х |
А2 | Х + 20 | 4 | 4(х + 20) |
5х = 4(х + 20); 5х = 4х + 80; х = 80.
Отже, v1 = 80 км/год.; v2 = 80 + 20 = 100 км/год.
Відповідь. 80 км/год.; 100 км/год.
№ 4. 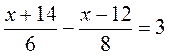 ; НСК (6; 8) = 24.
; НСК (6; 8) = 24. 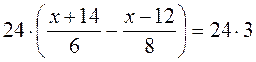 ;
;
4(х + 14) – 3(х – 12) = 72; 4х + 56 – 3х + 36 = 72; х = 72 – 92; х = -20.
Відповідь. -20.
№ 5. | Було | Змінили | Стало | |
Ш | 6х | -46 | 6х – 46 |
|
Е | X | -18 | Х – 18 | На 97 менше від |
(6х – 46) – (х – 18) = 97; 6х – 46 – х + 18 = 97; 5х – 28 = 97;
5х = 125; х = 125 : 5; х = 25.
Отже, на етажерці стояло 25 (книжок), а у шафі було 6 – 25 = 150 (книжок).
Відповідь. 150 книжок; 25 книжок.
№ 6. 5 |4 + 2(х – 3)| = 1; 5|4 + 2х – 6| =1; 5|2х – 2| = 1; |2х – 2| = 0,2;
2х – 2 = 0,2 або 2х – 2 = -0,2; х = 1,1 або х = 0,9.
Відповідь. 1,1; 0,9.
№ 7. 1) х = 5, отже, (2 + a) – 5 = 10; 2 + а = 2; а = 0;
2) лінійне рівняння виду ах = b не має коренів, якщо коефіцієнт при х дорівнює 0, a b? 0 (у нашому випадку). 2 + а = 0 (10 ? 0), отже, а = -2.
Відповідь. 1) 0; 2) -2.
Варіант 2
№ 1. х – 7 + 2 = 3х; х – 5 = 3х; -2х = 5; х = -2,5. x – 7 = 3(x – 1) + 1;
X – 7 = 3x – 3 + 1; x – 7 = 3x – 2; x – 3x = 7 – 2; -2x = 5; x = -2,5.
Корені рівнянь рівні, отже, рівняння є рівносильними.
Відповідь. Рівняння рівносильні, бо мають рівні корені.
№ 2. 0,4(2х – 7) + 1,2(3х + 0,7) = 1,6х; 0,8х – 2,8 + 3,6х + 0,84 = 1,6х;
4,4х – 1,96 = 1,6х; 4,4х – 1,6х = 1,96; 2,8х = 1,96; х = 1,96 : 2,8; х = 0,7.
Відповідь. 0,7.
№ 3. | V (км/год.) | T (год.) | S (км) |
А1 | X | 1,5 | 1,5х |
А2 | Х + 15 | 1,2 | 1,2(х + 15) |
1,5х = 1,2(х + 15); 1,5х = 1,2х + 18; 0,3х = 18; х = 18 : 0,3; х = 60.
Отже, v1 = 60 (км/год.), v2 = 60 + 15 = 75 (км/год.).
Відповідь. 60 км/год.; 75 км/год.
№ 4. 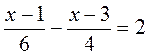 ; HCK (6; 4) = 12;
; HCK (6; 4) = 12; 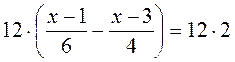 ;
;
2(x – 1) – 3(x – 3) = 24; 2x – 2 – 3x + 9 = 24; – x + 7 = 24; – x = 17; x = -17.
Відповідь. -17.
№ 5. | Було | Змінили | Стало | |
В | 5х | -58 | 5х – 58 |
|
Л | Х | -15 | Х – 15 |
(5x – 18) – (x – 15) = 61; 5x – 18 – x + 15 = 61; 4x – 3 = 61; 4x = 64; x = 16.
Отже, легкових автомобілів було 16, а вантажівок 5 – 16 = 80.
Відповідь. 80; 16.
№ 6. 2(|x| – 3) = 4|x| – 10; 2|x| – 6 = 4|x| – 10; -2|x| = – 4; |x| = 2; x = 2 aбo x = -2.
Відповідь. 2; -2.
№7. 1) Корінь х = 4, тому (а – 3) – 4 = 8; а – 3 = 2; а = 5;
2) рівняння виду ах = b не має коренів, якщо а = 0, b? 0; у нашому рівнянні а – 3 = 0; 8 ? 0, отже, а = 3.
Відповідь. 1) 5; 2) 3.
III. Підсумок уроку
Було б добре по закінченні виконання теоретичної контрольної роботи № 1 показати учням правильні розв’язання та відповіді (їх заздалегідь або записати за дошкою, або зробити копії та роздати всім учням).
IV. Домашнє завдання (випереджальне)
З пункту “Числові вирази” виписати нові поняття (невідомі) і знайти поняття (відомі), що використовуються під час пояснення матеріалу (§ 1 п.1).
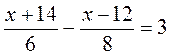 class=""/>.
class=""/>.
 на 61 більше
на 61 більше