Многочлен. Подібні члени многочлена та їх зведення. Стандартний вигляд многочлена. Степінь многочлена
Розділ 1. ЦІЛІ ВИРАЗИ
& 7. Многочлен. Подібні члени многочлена та їх зведення. Стандартний вигляд многочлена. Степінь многочлена
Вираз 7х2у3 – 5ху7 + 9х5 – 8 є сумою одночленів 7х2у3, -5ху7, 9×5 і -8. Цей вираз називають многочленом.
Одночлени, з яких складається многочлен, називають членами многочлена. Наприклад, многочлен 7х2y – 5ху7 + 9х5 – 8 складається із чотирьох членів: 7х2у3; 5ху7; 9х5 і 8.
Многочлен, який містить два члени, називають двочленом, многочлен, який містить три члени, – тричленом. Наприклад, а + b7, 2ху – 3y7 – двочлени;
У многочлені 7х2у + 8 + 9ху – 5х2у – 9 члени 7х2у і -5х2у є подібними доданками, оскільки вони мають одну й ту саму буквену частішу х2у. Також подібними доданками є й члени 8 і -9, які не мають буквеної частини. Подібні доданки многочлена називають подібними членами многочлена, а зведення подібних доданків у многочлені – зведенням подібних членів многочлена.
Приклад 1. Звести подібні члени у многочлені
7х2у + 8 + + 9ху – 5 х2у – 9.
Р о з в’ я з а н н я.
7х2у + 8 + 9ху – 5х2у – 9 = (7х2у – 5х2у) + (8 – 9) + 9ху = 2х2у – 1 + 9ху.
Кожний
Приклад 2. Чи записано в стандартному вигляді многочлени:
1) ху2 – х2у3х + 7;
2) m2 + 3mn – 3n2;
3) 9ab + 7 – 5ab?
Р о з в’ я з а н н я.
1) Оскільки х2y3x не є одночленом стандартного вигляду, то многочлен х2у – х2у3х + 7 не є многочленом стандартного вигляду.
2) Многочлен m2 + 3mn – 3n2 є многочленом стандартного вигляду.
3) Многочлен 9ab + 7 – 5ab містить подібні доданки, тому не є многочленом стандартного вигляду.
Приклад 3. Записати у стандартному вигляді многочлен
3х2ух + 5 – 4ху2у – 5х3у + 7ху3 – 8.
Р о з в’ я з а н н я. Спочатку зведемо до стандартного вигляду члени многочлена, потім зведемо подібні доданки:
3х2ух + 5 – 4ху2 – 5х3у + 7ху3 – 8 = 3х3у + 5 – 4ху3 – 5х3у + 7хУ3 – 8 = – 2х3у + 3ху3 – 3.
Члени многочлена 7m4р – 9 m2р4 + 3, що має стандартний вигляд, є одночленами відповідно п’ятого, шостого та нульового степенів. Найбільший із цих степенів називають степенем многочлена. Отже, 7m4 р – 9m2р4 + 3 є многочленом шостого степеня.
Наприклад, многочлени 5x: – 7 та 2а – 3b + 7 – першого степеня; многочлен 2mn + n – другого; 2х4 + x5 – х2 – п’ятого степеня.
Степенем довільного многочлена називають степінь тотожно рівного йому многочлена стандартного вигляду.
Приклад 4. Визначити степінь многочлена
2х2у + 3ху – 6х2у + 4х2у – 7.
Р о з в’ я з а н н я.
Спочатку запишемо многочлен у стандартному вигляді:
2х2у + 3ху – 6х2у + 4х2у – 7 = 3ху – 7. Многочлен 3ху -7 є многочленом другого степеня, а тому і многочлен 2х2у + 3ху – 6х2у + 4х2у – 7 є многочленом другого степеня.
Члени многочлена можна записувати в різній послідовності. Для многочленів стандартного вигляду, які містять одну змінну, члени, як правило, упорядковують за зростанням або спаданням показників степенів цієї змінної.
Наприклад, 7а4 + 5а3 – 8а2 – 5 або -5 – 8а2 + 5а3 + 7а4.
Будь-який многочлен є цілим виразом. Але не кожний цілий вираз є многочленом. Наприклад, цілі вирази 3(х – 1); (а + b)2; (m – n)3 не є многочленами, бо вони не є сумою одночленів.
Що називають многочленом? Що називають членами многочлена? Який многочлен називають двочленом, а який тричленом? Які члени многочлена називають подібними? Який многочлен називають многочленом стандартного вигляду? Що називають степенем многочлена?
186. (Усно) Які з даних виразів є многочленами:
1) m2(m – 5);
2) 3р2 – р2 + х7;
3) 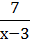 ;
;
4) b;
5) (а + 3)(а – 2);
6)n2 –  N;
N;
7)7,8;
8) (t – 3р)2!
187. Серед даних виразів виберіть многочлени:
1) p3 – p2 – p;
2) 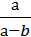 ;
;
3) с3;
4) a(a – b);
5) -3  ;
;
6) (х + 1)(х – 1);
7) а3 – 1;
8) (с + р)3.
188. Назвіть члени многочлена:
1) 3р2n – 5рn2 + 3 + 7рn;
2) – х3 + 5х2 – 9х + 7.
189. Складіть многочлен з одночленів:
1) 5m2, -2m і 3;
2) 7аb, -2а2 і b2;
3) 4р і 2q3;
4) – с2, -3mс, m3 і 7.
190. Складіть многочлен з одночленів:
1) 5m і -5n;
2) m3, -2m2 і mn;
3) – х3, -3у2, ху і 4.
191. (Усно) Чи записано многочлен у стандартному вигляді? Для многочленів стандартного вигляду визначте їх степінь.
1) 5m2 + m3 + 1;
2) 7х2 + 2х + 3х2;
3) 2 + а + а2b + 3;
4) с2с + с5 – 8;
5) 3х2х + 3хх2 + х;
6) р2 – 19.
192. Зведіть подібні члени многочлена:
1) 7х – 15ху – 8ху;
2) 8ab – 5ab + 4b2;
3) 9а4 – 5а + 7а2 – 5а4 + 5а;
4) 18а4b – 9а4b – 7bа4;
5) 4b3 + b2 – 15 – 7b2 + b3 – b + 18;
6) 9ху2 – x3 – 5ху2 + 3х2у – 4ху2 + 2×3.
193. Зведіть подібні члени многочлена:
1) а3 – 2а3 + 3а3;
2) – х4 + 2х3 – 3х4 + 5х2 – 3х2;
3) 7 + 3m6 – 2m3 – m6 + 2m6 – m5 – 7;
4) 9ху3 + 6х2у2 – x3у + х2у2 – 9ху3.
194. (Усно) Які з многочленів є многочленами четвертого степеня:
1) а3 + 3а2 + 1;
2) а2а2 – 8;
3) а4 – 4а3 – а4;
4) аа3 + 2?
195. Які з многочленів є многочленами п’ятого степеня:
1) m3 + m4 – m2;
2) 12 + mm4;
3) mm + mm2 + m2m2;
4) m5 – 3 – m5?
196. Зведіть многочлен до стандартного вигляду та визначте його степінь:
1) х2у + хуу;
2) 2a ∙ а2 – 3b + а ∙ 5с;
3) 7х ∙ 5y2 – 4у ∙ 7х2;
4) 3а ∙ 4а ∙ (-5а) – а3 ∙ ( 8b).
197. Подайте многочлен у стандартному вигляді та визначте його степінь:
1) 3х ∙ х2 + 2х ∙ 5у2;
2) 5а ∙ b2а + Зb ∙ 2аb2;
3) -5mn3m + 4mmm;
4) 5р ∙ 3р ∙ (-р) – p ∙ qp.
198. Перепишіть многочлен в порядку спадання степенів змінної:
1) 7х – 5х3 + х4 – 9х2 + 1;
2) 8у3 – 5 + 7у6 – 9у4 + у2.
199. Перепишіть многочлен в порядку зростання степенів змінної.
1) 3m2 – 3m + m3 – 8;
2) 7а2 – 9а5 + 4а3 + 5 – а4.
200. Знайдіть значення:
1) двочлена 3×2 – 1, якщо х = -1; 2;
2) тричлена 5m + 9n2 – 1, якщо m = -2, n =  .
.
201. Обчисліть значення многочлена:
1) 64×3 – х2 + 1, якщо x =  ;
;
2) 4mn – 3m + 2n – 4mn, якщо m = 4, n = -3.
202. Обчисліть значення многочлена:
1) 9р2 – р3, якщо р =  ;
;
2) 2ху – 4х + 3у + 4x, якщо x = -1, у – 2.
203. Чи існує таке значення х, при якому значення многочлена х2 + 5 дорівнює нулю; є від’ємним?
204. Зведіть многочлен до стандартного вигляду і вкажіть його степінь:
1) 3а2аb – 5а2b2b2 – 6аb ∙ 2а + 5аb ∙ 0,4аb – 1,5а ∙ 2b ∙ а2;
2) 3ху2 ∙ 4х3у + 5х3у ∙ 2у ∙ (-х) – 10х3у3∙  Х – 7ху ∙ (-3ху3).
Х – 7ху ∙ (-3ху3).
205. Зведіть многочлен до стандартного вигляду і вкажіть його степінь:
1) 3а2b3 – ab3 – а3а – а2b2 ∙ b + 0,5аb ∙ 2b2 + 4ab ∙ 0,5аb2;
2) 7х ∙ 2у3 – 5х ∙ 3ху ∙ (-x) +  Y ∙ (14xy) – 3ух ∙4y2.
Y ∙ (14xy) – 3ух ∙4y2.
206. Зведіть многочлен 5хy + х2у2 – 2х3у – 3ху3 – х2у2 до стандартного вигляду і знайдіть його значення, якщо х =  , у = -1.
, у = -1.
207. Доведіть, що многочлен а2 + b2 + 1 при будь-яких значеннях змінних а і b набуває лише додатних значень.
208. Запишіть замість зірочки такий одночлен, щоб утворився многочлен четвертого степеня:
1) х3 + 3х2 + * – 2;
2) m6 – 4m4 + mn + *;
3) а3b – 3а4b3 + 3а2 + *;
4) pq3 – p2q2 + p2q3 + * – p3q.
209. Запишіть замість зірочки такий одночлен, щоб після зведення до стандартного вигляду одержати многочлен, що не містить змінної х:
1) 3х – 12 + 5х + 15 – 9х + *;
2) 5ху2- у3 + 7у2 + 7у2х – 5 + *.
210. Дано многочлен 5х3 + 2х2 – х + 7. Утворіть з нього повий многочлен, замінивши змінну х на одночлен:
1) m;
2) – х;
3) 2а;
4) 3b2.
Отримані многочлени зведіть до стандартного вигляду.
211. Дано многочлен 3а3 – 5а2 + а – 8. Утворіть з нього новий многочлен, замінивши змінну а на даний одночлен, та зведіть до стандартного вигляду:
1) х;
2) – а;
3) 2b;
4) 3с2.
212. Оберіть ті многочлени, значення яких є додатними при будь-яких значеннях змінних, щодо нього входять; є від’ємними при будь-яких значеннях змінних, що до нього входять:
1) а4 + 3а2 + 5;
2) с5 + с3 + с;
3) – р2 – 7;
4) – m2 – m2n2 – n2 – 9;
5) – а – b – 7;
6) х8 + у8 + с4 = 1.
Вправи для повторення
213. Розкрийте дужки і спростіть вираз:
1) х + 5 + (2х – 7);
2) 2у – 7 – (3у – 8);
3) 7 – (2х + 9) + (3х – 11).
214. Складіть числовий вираз і знайдіть його значення:
1) сума квадратів чисел 3,1 і -2,7;
2) квадрат різниці чисел -3,8 і -3,7;
3) куб суми чисел 1,52 і -1,5.
215. Замініть пропуски степенем з основою х так, щоб одержати тотожність:
1) х3 ∙ ( … )2 = х13;
2) ( … )3 ∙ х7 = х19.
Цікаві задачі для учнів неледачих
216. Чи існують такі натуральні значення змінних х і у, при яких х5 + у3 = 336?