Головна ⇒ 📌Довідник з геометрії ⇒ Множення вектора на число
Множення вектора на число
Геометрія
Вектори
Множення вектора на число
Добутком вектора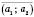 На число
На число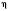 називається вектор
називається вектор 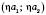 , тобто
, тобто 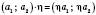 . Для будь-якого вектора
. Для будь-якого вектора  і чисел
і чисел 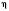 і
і 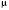
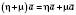 .
.
Для будь-яких двох векторів 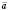 і
і 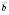 і числа
і числа 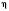
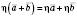 .
.
Теорема
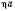 дорівнює
дорівнює 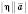 . Напрям вектора
. Напрям вектора 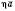 , якщо
, якщо 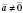 , збігається з напрямом вектора
, збігається з напрямом вектора 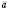 , якщо
, якщо 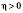 , і протилежний напряму вектора
, і протилежний напряму вектора 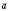 , якщо
, якщо 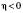 .
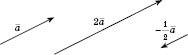
.Приклад. На рисунку зображені вектори
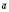 ,
, 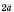 і
і 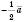 :
:
Теорема 2. Два ненульові вектори
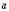 і
і 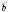
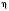 таке, що
таке, що 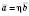 .
.Теорема 3. Ненульові вектори
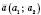 і
і 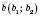 колінеарні тоді й тільки тоді, коли їх відповідні координати пропорційні, тобто
колінеарні тоді й тільки тоді, коли їх відповідні координати пропорційні, тобто 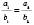 .
.Теорема 4. Якщо
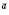 і
і 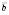 – відмінні від нуля неколінеарні вектори, то будь-який вектор
– відмінні від нуля неколінеарні вектори, то будь-який вектор 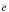 можна записати у вигляді
можна записати у вигляді 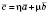 .
.Related posts:
- Множення вектора на число УРОК № 47 Тема. Множення вектора на число Мета уроку: формування вміння множити вектор на число; вивчення властивостей множення вектора на число; формування вмінь застосовувати вивчені значення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині”[13]. Вимоги до рівня підготовки учнів: описують множення вектора на число; […]...
- Вектори в просторі (рівність векторів, колінеарність векторів, компланарність векторів). Додавання, віднімання векторів, множення вектора на число, властивості дій над векторами Урок 58 Тема. Вектори в просторі (рівність векторів, колінеарність векторів, компланарність векторів). Додавання, віднімання векторів, множення вектора на число, властивості дій над векторами Мета уроку: формування знань учнів про вектори в просторі, дії над векторами, заданими координатами, Формування вмінь застосовувати вивчений матеріал до розв’язування задач. Обладнання: схема “Вектори в просторі”. Хід уроку І. Перевірка домашнього […]...
- Вектори у просторі – ВЕКТОРИ Формули й таблиці МАТЕМАТИКА ВЕКТОРИ Вектори у просторі Вектор – спрямований відрізок А – початок вектора В – кінець вектора Модуль вектора – довжина відрізка, який зображує вектор: ||. Два вектори рівні, якщо вони однаково спрямовані і мають рівні модулі. Координати вектора з початком у точці А(x1,y1,z1) і кінцем у точці В(х2,у2,z2). Рівні вектори мають […]...
- Вектор. Модуль і напрям вектора. Рівність векторів УРОК № 42 Тема. Вектор. Модуль і напрям вектора. Рівність векторів Мета уроку: формування понять вектора, модуля вектора, напряму вектора; рівності векторів; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують вектор, модуль і […]...
- Розкладання вектора за координатними осями Геометрія Вектори Розкладання вектора за координатними осями Вектор називається Одиничним, якщо його абсолютна величина дорівнює одиниці. Одиничні вектори, які мають напрями додатних координатних півосей, називаються Координатними векторами, або Ортами (див. рисунок). Позначення: ; . Оскільки координатні вектори відмінні від нуля й неколінеарні, то будь-який вектор можна розкласти за цими векторами: ....
- Координати вектора УРОК № 43 Тема. Координати вектора Мета уроку: формування поняття координат вектора та вміння застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують координати вектора; застосовують вивчені означення і властивості до розв’язування задач. Хід уроку I. […]...
- Координати вектора. Дії над векторами, що задані координатами 1. Запишемо координати вектора: 1) 2) 3) 4) 2. 1) 2) 3) 4) 5) 6) 3. 1) Запишемо розклад за координатними векторами: 2) Запишемо розклад за координатними векторами: 3) Запишемо розклад за координатними векторами: 4) Знайдемо координати векторів : Знайдемо координати вектора Запишемо розклад за координатними векторами: 5) Знайдемо координати векторів Знайдемо координати вектора Запишемо […]...
- Колінеарні вектори УРОК № 48 Тема. Колінеарні вектори Мета уроку: формування поняття “колінеарні вектори”; вивчення властивості та ознаки колінеарних векторів; формування вмінь учнів застосовувати вивчені означення та властивості до розв’язування завдань. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують колінеарність векторів; застосовують вивчені означення та […]...
- Додавання векторів Геометрія Вектори Додавання векторів Сумою векторів і називається вектор . Додавання векторів має переставну та сполучну властивості: ; для будь-яких , , . Теорема. Які б не були точки A, B, C, справджується векторна рівність: . Правило трикутника додавання векторів Щоб знайти суму довільних векторів і , треба від кінця вектора (див. рисунок) відкласти вектор […]...
- Вектори в просторі – Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Вектори в просторі Усі основні означення векторів у просторі залишаються такими самими, як означення векторів на площині (див. розділ “Геометрія. 8 клас”). Координатами вектора , де , , називають числа, , . Вектори рівні тоді, й тільки тоді, коли вони мають відповідно рівні координати. Це дає підставу позначити […]...
- Координати векторa Геометрія Вектори Координати векторa Нехай вектор має початком точку , а кінцем – точку . Координатами вектора називаються числа і . Позначення: або . . Очевидно, що . Теорема. Вектори рівні тоді й тільки тоді, коли вони мають рівні відповідні координати....
- Проекція вектора на координатну вісь – Елементи векторної алгебри 3. Елементи векторної алгебри 3.5. Проекція вектора на координатну вісь Довжину відрізка A1B1 між проекцією початку вектора а і кінця вектора на вісь, взяту зі знаком ” + ” або “-“, називають проекцією вектора на координатну вісь. Проекція додатна, коли напрям руху від проекції початку вектора до проекції кінця збігається із напрямом координатної осі, і […]...
- Множення вектора на скаляр – Елементи векторної алгебри 3. Елементи векторної алгебри 3.4. Множення вектора на скаляр Приклад: а – 4...
- Скалярний добуток векторів Геометрія Вектори Скалярний добуток векторів Скалярним добутком векторів і називається число . Позначення: . . Очевидно, що . Розподільна властивість скалярного добутку: . Кутом між ненульовими векторами і називається кут BAC. Кутом між будь-якими двома ненульовими векторами і називається кут між векторами, що дорівнюють даним і мають спільний початок. Вважають, що кут між однаково напрямленими […]...
- Алгебра векторів 1. Побудуємо вектори – одиничний вектор 2. Побудуємо вектори 3. Побудуємо вектори 4. Побудуємо вектори 5. 6. 1) Побудуємо вектори 2) Побудуємо вектори 7. Побудуємо вектори 8. 1) 2) 9. Побудуємо вектори Вектори та рівні. 10. Накреслимо два ненульові вектори Побудуємо Побудуємо Таким чином, 11. Побудуємо вектори Вектори протилежно напрямлені. 12. Побудуємо вектори 13. 1) […]...
- Тематична контрольна робота № 5 УРОК № 51 Тема. Тематична контрольна робота № 5 Мета уроку: контроль навчальних досягнень учнів з мети “Вектори”. Тип уроку: комбінований. Вимоги до рівня підготовки учнів: застосовують означення та властивості геометричних фігур при розв’язуванні задач. Хід уроку І. Тематичне оцінювання № 5 Тематичне оцінювання № 5 можна провести у вигляді тематичної контрольної роботи. Наводимо текст […]...
- Скалярний добуток векторів УРОК № 49 Тема. Скалярний добуток векторів Мета уроку: формування поняття скалярного добутку векторів; формування вмінь застосовувати вивчені означення та властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині”[13]. Вимоги до рівня підготовки учнів: формулюють означення скалярного добутку, його властивості; застосовують вивчені означення та властивості до розв’язування […]...
- Кут між векторами. Скалярний добуток векторів Урок 59 Тема. Кут між векторами. Скалярний добуток векторів Мета уроку: формування понять кута між векторами, скалярного добутку векторів. Формування вмінь учнів застосовувати вивчений матеріал до розв’язування задач. Обладнання: схема “Вектори в просторі” Хід уроку 1. Фронтальна бесіда з класом за контрольними запитаннями № 18- 20 з використанням схеми “Вектори в просторі” (див. с. 233). […]...
- Додавання векторів УРОК № 44 Тема. Додавання векторів Мета уроку: формування вміння додавати вектори, вивчення властивостей суми векторів; формування вмінь застосовувати вивчені властивості й означення до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують додавання векторів; відкладають вектор, що дорівнює сумі векторів; формулюють […]...
- Письмове множення на двоцифрове число. Задачі на застосування дії множення на двоцифрове число (№№ 102-111) Тема. Письмове множення на двоцифрове число. Задачі на застосування дії множення на двоцифрове число (№№ 102-111). Мета. Ознайомити учнів з письмовим множенням на двоцифрове число; формувати уміння розв’язувати складені задачі, нерівності; розвивати логічне мислення, математичне мовлення. Обладнання. Таблиця усних обчислень; таблиця “Письмове множення на цифрове число”; схеми задач; сигнальні картки; “Картки для поточного контролю знань”. […]...
- Додавання векторів – Елементи векторної алгебри 3. Елементи векторної алгебри Векторні величини (вектори) – це величини, які характеризуються числовими значеннями і напрямом: Скалярні величини (скаляри) – це величини, які характеризуються лише числовим значенням. Вони можуть бути додатними та від’ємними й додаються алгебраїчно. 3.1. Додавання векторів Якщо вектори спрямовані вздовж однієї прямої або якщо вони паралельні, то результуючий вектор дорівнює алгебраїчній сумі […]...
- Віднімання векторів УРОК № 45 Тема. Віднімання векторів Мета уроку: формування вмінь віднімати вектори, вивчення властивостей різниці векторів; формування вмінь застосовувати вивчені означення та властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині”[13]. Вимоги до рівня підготовки учнів: описують віднімання векторів; відкладають вектор, що дорівнює різниці векторів; формулюють властивості […]...
- ПИСЬМОВЕ МНОЖЕННЯ НА ДВОЦИФРОВЕ ЧИСЛО. ЗАДАЧІ НА ЗАСТОСУВАННЯ ДІЇ МНОЖЕННЯ Мета: закріпити вміння учнів виконувати письмове множення на двоцифрове число; розвивати мислення, вміння аналізувати задачі, творчо працювати над ними; виховувати інтерес до предмета. ХІД УРОКУ I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. КОНТРОЛЬ, КОРЕКЦІЯ І ЗАКРІПЛЕННЯ ЗНАНЬ 1. Перевірка домашнього завдання 2. Усні обчислення Гра “Ланцюжок” – До числа 270 додати 100; відняти 300; зменшити на 60; зменшити […]...
- МНОЖЕННЯ НА ОДНОЦИФРОВЕ ЧИСЛО ПИСЬМОВЕ МНОЖЕННЯ БАГАТОЦИФРОВОГО ЧИСЛА НА ОДНОЦИФРОВЕ МНОЖЕННЯ НА ОДНОЦИФРОВЕ ЧИСЛО 590. Використовуючи правило множення суми на число, продовж обчислення з поясненням. 324 ∙ 2 = (300 + 20 + 4) ∙ 2 = 300 ∙ 2 + … 4 123 ∙ 2 = (4 000 + 100 + 20 + 3) ∙ 2 = … […]...
- ПИСЬМОВЕ МНОЖЕННЯ НА РОЗРЯДНЕ ЧИСЛО ПИСЬМОВЕ МНОЖЕННЯ І ДІЛЕННЯ НА ДВОЦИФРОВЕ ЧИСЛО ПИСЬМОВЕ МНОЖЕННЯ НА РОЗРЯДНЕ ЧИСЛО 249. Назви і випиши окремо розрядні одиниці й розрядні числа. 1 28 20 50 10 90 120 100 400 250. Виконай дії з розрядними одиницями. А) 3 ∙ 1 8 ∙ 10 20 ∙ 10 6 ∙ 100 14 ∙ 10 1 ∙ […]...
- Письмове множення на двоцифрове число Мета: формувати навички письмового множення на двоцифрове число. Тип уроку: засвоєння нового матеріалу Дидактичні задачі. Вдосконалювати навички усних обчислень (РЗ ч. 1 с. 24, №1). Актуалізувати усні прийоми множення двоцифрового числа на одноцифрове, одноцифрового числа на двоцифрове; актуалізувати знання правила множення числа на суму ( №1). Актуалізувати знання розрядного складу числа (РЗ ч. 1 с. […]...
- Прискорення. Прискорення при криволінійному русі – КІНЕМАТИКА ФІЗИКА Частина 1 МЕХАНІКА Розділ 1 КІНЕМАТИКА 1.3. Прискорення. Прискорення при криволінійному русі Градієнт швидкості матеріальної точки V з часом £ характеризують прискоренням Прискорення виражається в метрах на секунду в квадраті (СІ) та сантиметрах на секунду в квадраті (СГС). При прямолінійному русі вектор швидкості напрямлений уздовж однієї й тієї самої прямої – траєкторії, внаслідок чого […]...
- Письмове множення і ділення на кругле число Мета: формувати навички письмового множення та ділення на кругле число. Тип уроку: закріплення та застосування знань, умінь та навичок Дидактичні задачі. Вдосконалювати навички усних обчислень (№1; РЗ ч. 1 с. 24, №1). Закріплювати прийом письмового множення на кругле число ( №2); ділення на кругле число ( №3; РЗ ч. 1 с. 24, №2). Формувати уміння […]...
- АЛГОРИТМ МНОЖЕННЯ НА ДВОЦИФРОВЕ ЧИСЛО ПИСЬМОВЕ МНОЖЕННЯ І ДІЛЕННЯ НА ДВОЦИФРОВЕ ЧИСЛО АЛГОРИТМ МНОЖЕННЯ НА ДВОЦИФРОВЕ ЧИСЛО 287. Продовж обчислення. Поясни спосіб обчислення. 23 ∙ 25 = 23 ∙ (20 + 5) = … 23 ∙ 20 = … 23 ∙ 5 = … 34 ∙ 14 = 34 ∙ (10 + 4) = … 34 ∙ 4 = … […]...
- ОПЕРАЦІЇ З ВЕКТОРНИМИ ВЕЛИЧИНАМИ Фізика підготовка до ЗНО комплексне видання МЕХАНІКА 1. ОСНОВИ КІНЕМАТИКИ 1.2. ОПЕРАЦІЇ З ВЕКТОРНИМИ ВЕЛИЧИНАМИ Вектор – напрямлений відрізок. Векторні величини мають числове значення (модуль), напрям, точку прикладання (рис. 3). Рис. З Проекція вектора на вісь Ох – довжина відрізка, який сполучає проекцію початку вектора на вісь Ох з проекцією кінця вектора на ту саму […]...