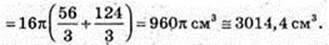Об’єми і площі поверхонь геометричних тіл
289.
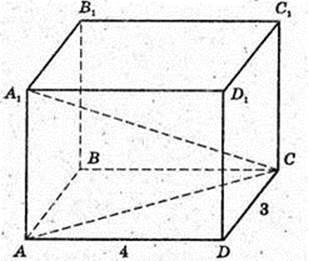
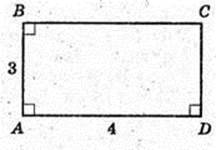


1) ABCDA1B1C1D1 – прямокутний паралелепіпед.
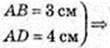
AC = 5 см. A1C = 15 см.
ΔAA1C: ∠ A = 90°.
Відповідь:
2) V – ? Δ AD1CD: DC = 3, D1C = 5 → DD1 = 4.
V= 3 × 4 × 4 = 48см3.
Відповідь: 48 см3,
3) ABCDA1B1C1D1 – прямий паралелепіпед.
А1D = 4см.
290.
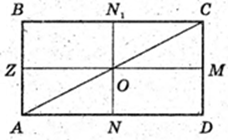
ABCDA1B1C1D1 – прямий паралелепіпед.
1) PAA1B1B = 2(AB + AA1) = 10 см; РАВСD = 2(АВ + АВ) = 6 см.
РАA1D1D = 2(АА1 + АD) = 8 см. Нехай AB = х, AD = у, АА1 = z;
X – ? у – ? z – ?
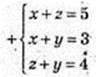
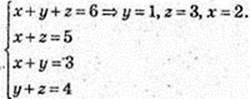
2(х + y + z) = 12,
V= x × у × z = 1 × 3 × 2 = 6 см3.
Відповідь: V = 6 см2.
2) ABCDA1B1C1D1 – прямокутний паралелепіпед.
A1C = 6 см. AA1 : AB : AD = 3 : 2 : 1.
V – ? AA = 3k, AB = 2k, AD = k.
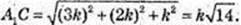
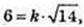
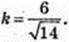
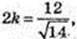
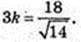
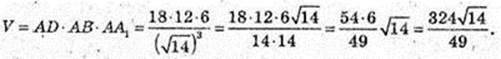
Відповідь:
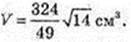
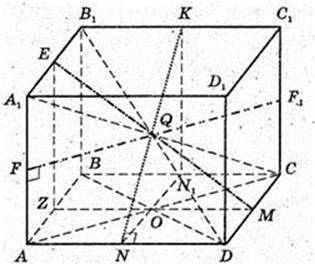
3) Q – центр симетрії паралелепіпеда.
Відстані до ребер AA1 дорівнює QF=9 см. V – ?
AD = QN = 8 см, DC = QM = 7 см. QF = OA = 9,
AB = x, AD=y, AA1 = z.
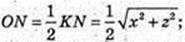
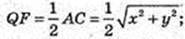
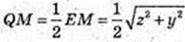
Маємо:
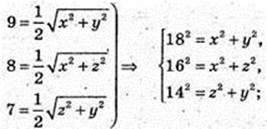
182 + 162 + 142 = 2(х2 + у2 + z2);
(х2 + у2 + z2) × 2 = 182 + 162 + 142;
182 + 162 + 142 = 2(х2 + у2 + z2) → 182 + 16s + 142 = 2 × 182 + 2z2 → 2z2 =
= 162 + 142 – 182 = 128: z = 8.
2(y2 + 162) = 182 + 162 + 142;
2у2 = 182 + 142 – 162 = 2 × 132;
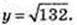 2(х2 + у2 + z2) = 142 + 162 + 182;
2(х2 + у2 + z2) = 142 + 162 + 182;
2(х2 + 142) = 142 + 162 + 182; 2×2 = 162 + 182 – 142;
2х2 = 384; х2 = 192 = 4 × 48 = 4 × 16 × 3; 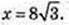
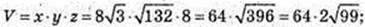
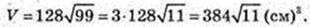
Відповідь: 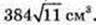
4)
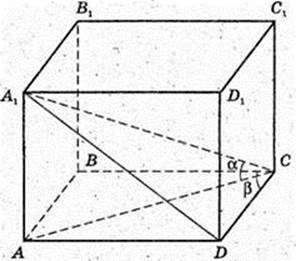
Діагональ прямокутного паралелепіпеда ABCDA1B1C1D1 дорівнює d,
A1C = d. ∠A1CA = α, ∠A1CB = β. V – ?
ΔAA1C: ∠A = 90°, A1C = d, ∠A1CA = α. AA1 = A1C × sin α,
AC = A1C × cos α; AA1 = d sin α, AC = d cos α.
ΔA1CD: ∠A1DC = 90°, ∠A1CD = β. CD = A1C × cos β, CD = d cos β.
ΔACD: AD = 90°, 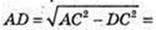
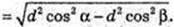
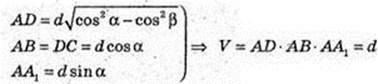
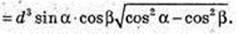
Відповідь: 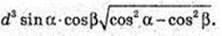
291.
ABCA1В1С1 – правильна трикутна призма. AB = BC = AC.
1) 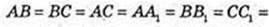
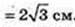 V – ?
V – ?
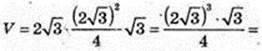
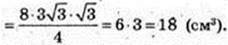
Відповідь: 18 см3.
2) AA1 = 3 см. 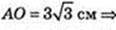
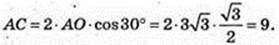
AC = 9, 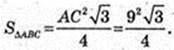
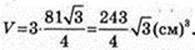
3) 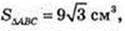 H = 3а, тобто AA1 = 3АВ. V – ?
H = 3а, тобто AA1 = 3АВ. V – ?
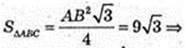
AB2 = 36, AB = 6 → H= 18 см.
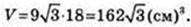
Відповідь: 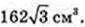
4) AC1 = a. ∠C1AC = α. V – ?
AC = AC1 cos α; C1C =AC1 sin α; AC = а cos α; H = a sin α.
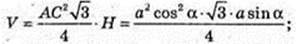
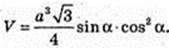
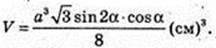
Відповідь: 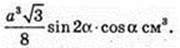
5) AA1C1C – квадрат, H = a, AB = a, V-?
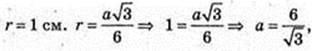
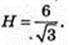
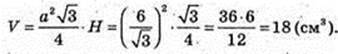
Відповідь: 18 см3.
6) AA1 = BD. BD + AC в площині ABC. SDD1B1B = 12 см2. V-?
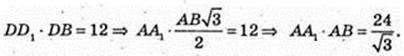
AA1 = BD. 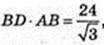
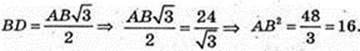
Але 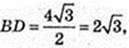
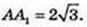
V = 24 см3. AB2 = 16. AB = 4.
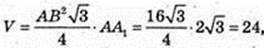
Відповідь: 24 см3.
7) 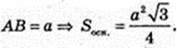 V-? H – ?
V-? H – ?
Якщо в призму можна вписати кулю, то висота призми удвічі більше радіуса кола, вписаного в основу призми. H = 2r, 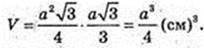
Відповідь:
292.
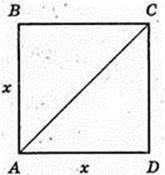
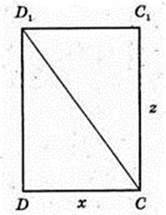
ABCDA1B1C1D1 – правильна чотирикутна призма.
1) A1C = 13 см, BC =12 см. V – ?
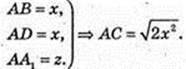
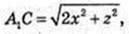
Маємо: 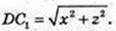
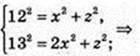
132 = х2 + 122 → x2 = 25, х = 5 → 22 = 122 – 52 = 7 × 17;
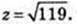
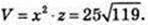
Відповідь: 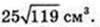
2) DC1 = 8 см, ∠C1DA1 = 60°. З умови DA = DC → DA1 = DC1.
ΔA1C1D: ∠D = 60° і DA1 = DC1 → A1C1 = C1D = A1D = 8 см.
AC = 8, 2х2 = 82 → x2 = 32, 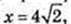
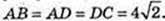
ΔDC1C: ∠C = 90°, DC1 = 8, 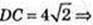
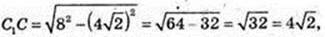
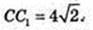
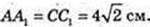
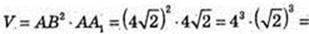
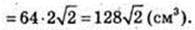
Відповідь: 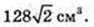
3)
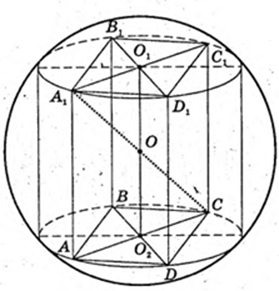
ABCBA1B1C1B1 – правильна чотирикутна призма.
SAA1C1C = S. A1C = d. V – ? VAA1B1C1D1DCBA – ? AB = x,
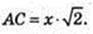 AA1 = z.
AA1 = z.
ΔA1CA: ∠A = 90°, A1C = d, d2 = 2х2 + z2.
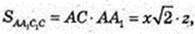
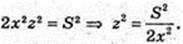
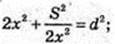
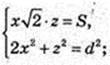
4×4 – 2x2d2 + S2 = 0; x – ? z – ?
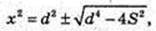
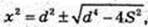
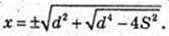
Але X2 ≥ 0.
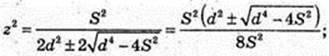 або
або
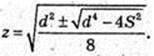
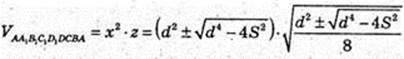
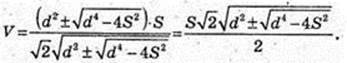
Відповідь: 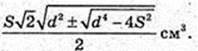
293.
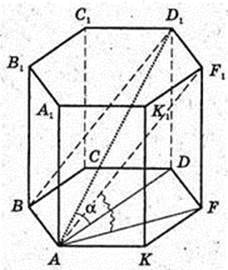
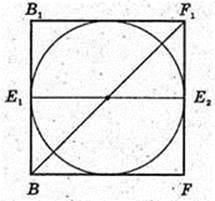
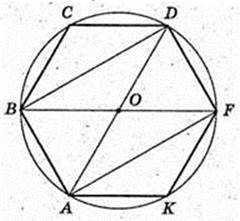
ABCDFKA1B1C1D1F1K1 – правильна шестикутна призма.
1) Всі ребра дорівнюють 1 м. V-?V=1см3.
2)AB = 1 м. AB = BC = CD = DF = FK = KA.
В призму можна вписати кулю. V – ?
BF = 2AB = 2. 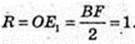 H = 2R = 2.
H = 2R = 2.
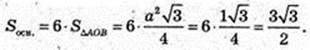
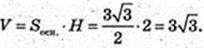
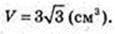
Відповідь: 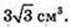
3) AD1 = d. ∠D1AD = α. V – ?
ΔAD1D: ∠D = 90°, ∠A = α, AD1 = d = D1D = d sin α → H = d sin α.
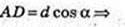
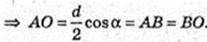
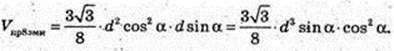
Відповідь: 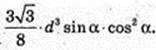
4) Переріз призми ABD1F1, ABD1F1 – прямокутник.
SABD1F1 =S. ∠F1AF = α. V – ?
S = AB × AF1, 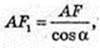 AF – ?
AF – ?
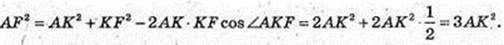
AF2 = 3AK2 = 3АВ2;
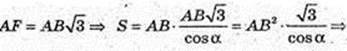
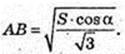
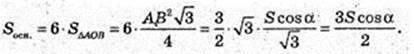
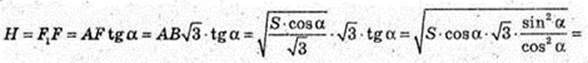
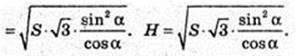
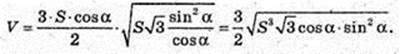
Відповідь: 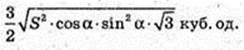
294.
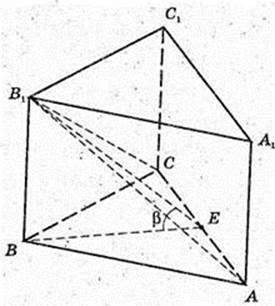
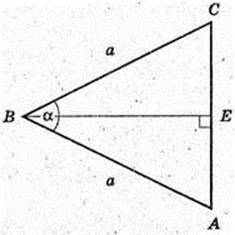
ABCA1B1C1 – пряма призма.
1) ΔABC – рівнобедреник, AB = BC = а.
∠ABC = a. V – ?
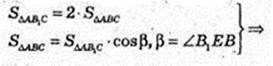
S ΔABC = 2 × S ΔABC × cos β; 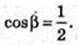
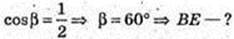 B1B – ?
B1B – ?
ΔАВС: a =AB = СВ,
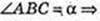
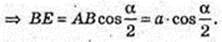
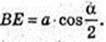
ΔBB1E: ∠B = 90°,
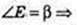
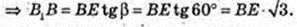
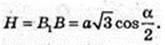
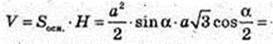
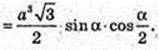
Відповідь: 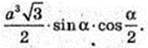
2)
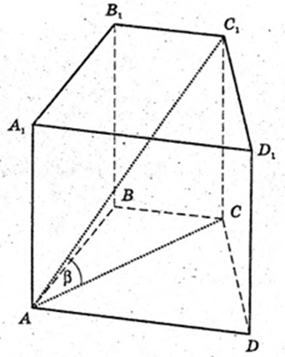
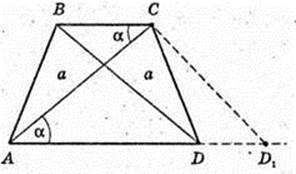
ABCDA1B1C1D1 – пряма призма.
ABCD – трапеція, BC? AD. AB = CD, AC = BD = a. ∠C1AC = β, ∠CAD = α.
V – ? Sосн. – ? CD1? BD, CD1 =NAC, ∠D1AC = α.
ΔD1AC: ∠ACD1 = 180° – 2α, sin(180° – 2α) = sin 2α.
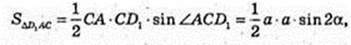
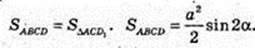 H-?
H-?
H = C1C = AC tg β = а tg β.
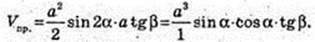
Відповідь: 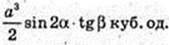
3)
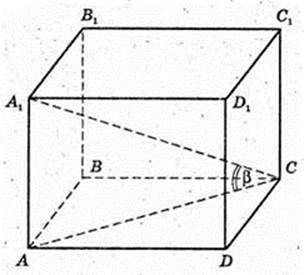
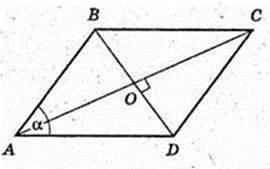
ABCDA1B1C1D1 – пряма призма. ABCD – ромб. ∠DAB = α.
A1C = l, ∠A1CA = β. Vпр. – ?
ΔА1СА: ∠A = 90°, ∠C = β, A1C = l → A1A = A1C × sin β = I sin β;
A1A = = I sin β. A1A = H; AC =A1C × cos β = I cos β. AC = I cos β.
ABCD – ромб. SABCD – ? AD – ?
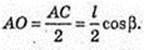
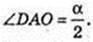
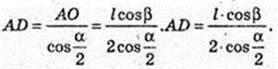
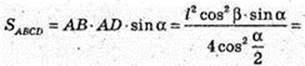
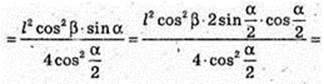
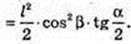 V = A1A × SABCD.
V = A1A × SABCD.
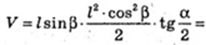
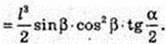
Відповідь: 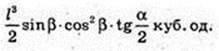
4)
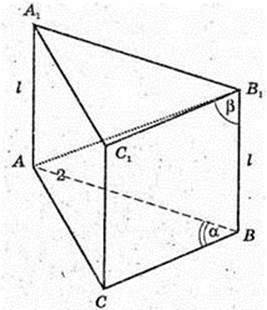
ABCA1B1C1 – пряма призма.
AA1 = I. ∠AB1B = β, ∠ACB = 90°,
∠ABC = α. V – ? AB – ? CB – ?
ΔAB1B: ∠B1BA = 90°, B1B = I, ∠AB1B = β. AB = l tg β.
ΔΑ BC: ∠C = 90°, ∠ABC = α → CB =AB cos α = l tg β cos α.
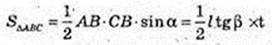
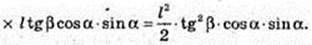
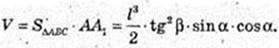
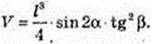
Відповідь: 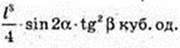
295.
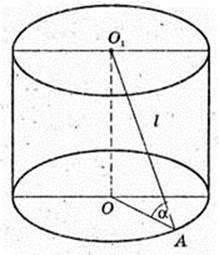
Прямий круговий циліндр. O1A = I, O1O = H, ∠O1AO = φ. V – ?
O1A = l, O1O = Н, ∠O1AO = φ. V – ?
1) 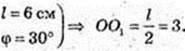
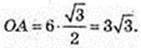
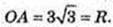 SOCH = πR2 = 27π. V = 27π × 3 = 81π.
SOCH = πR2 = 27π. V = 27π × 3 = 81π.
Відповідь: 81π см3.
2)
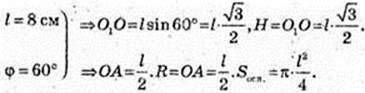
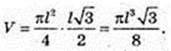
Відповідь: 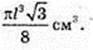
3)
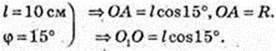
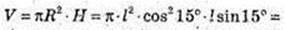
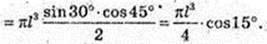
Відповідь: 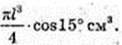
296.
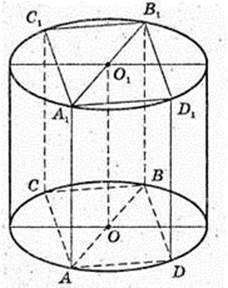
Прямий круговий циліндр. V – ?
1) AA1B1B – квадрат. SAA1B1B = AB2 = S,
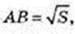
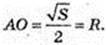
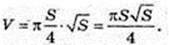
Відповідь: 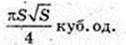
2) В циліндр вписана правильна чотирикутна призма AA1D1B1C1CBD.
ACBD – квадрат, AC = CB = BD =AD = a. AA1 = h. V-? V= a2h.
Відповідь: a2h куб. од.
3)
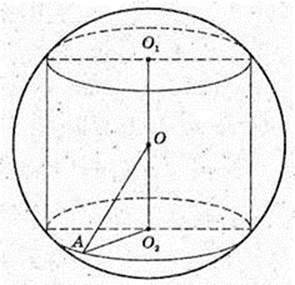
Циліндр вписаний в кулю радіусом її. V – ?
OA = R, O2A = r. г – ?
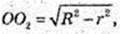
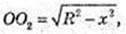 r = х.
r = х.
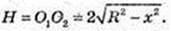
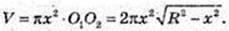
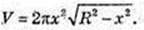
Х – ? V найб. – ? х – ? V′ = 0,
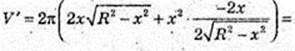
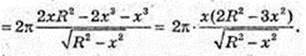
V′ = 0, якщо 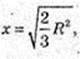
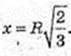
V′(х) > 0, якщо 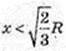 і V′(х) < 0, якщо
і V′(х) < 0, якщо 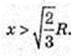
В т. 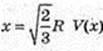 приймає найбільше значення.
приймає найбільше значення.
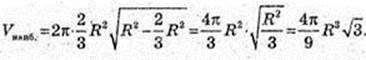
Відповідь: 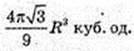
4)
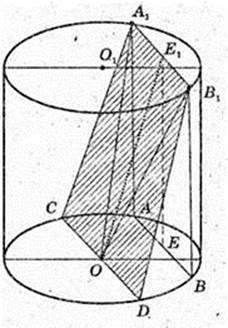
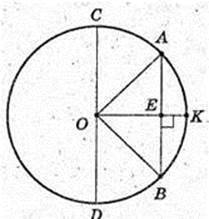

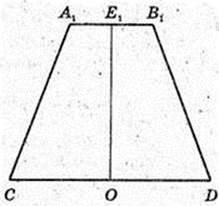
Прямий круговий циліндр.
Переріз CA1B1D, A1E1 = E1B1, CO = OD, CA1 = DB1, V – ?
A1B1 ? CD. CA1B1D – трапеція, A1B1 ? CD, CA1 = DB1.  AKB = α, ∠AOB = α. AB = а. ΔАОВ: OA = OB = R. OE + AB, AE = ЕВ.
AKB = α, ∠AOB = α. AB = а. ΔАОВ: OA = OB = R. OE + AB, AE = ЕВ.
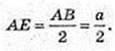 ∠AOB = α,
∠AOB = α, 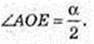
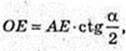
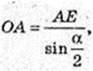
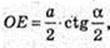
ΔOE1E: ∠E = 90°, E1E – ? ∠B = φ.
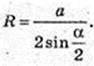
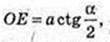
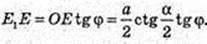
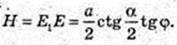
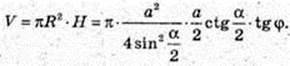
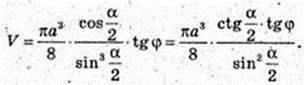
Відповідь: 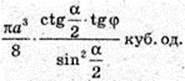
297.
Цистерна має форму, циліндра, H = 4,8 м, 2R= 1,4 м
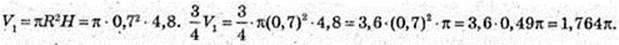
Відповідь: 1,764π куб. од.
298.

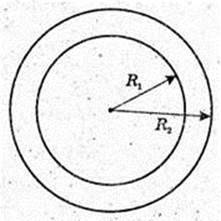
R1 = 0,65 см. R2 = 0,65 см + 0,4 см = 1,05 см.
V = πR22 × L – πR21 × L = Πl(R22 – R21) = 2500π(1,052 – 0,652) = 2500π(1,05 – 0,65) х × (1,05 + 0,65) = 2500π × 0,4 × 1,7= 1700π.
М = ρ × V = 11,4 × 1700π (г) = 16 кг.
299.
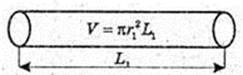
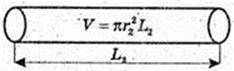
Знайдемо об’єм дроту. M = ρ × V, 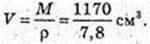
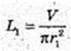
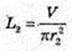
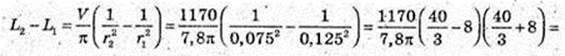
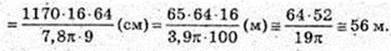
300.
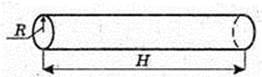
V = πR2 × Η. 15 = π × 0,0752 ×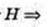
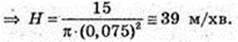
301.
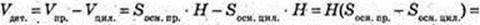
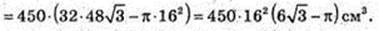
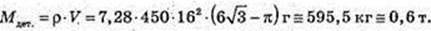
302.
V – ? V1- ? H = 4,5 м, 2 R = 1,6 м. V = π × 0,82 = 4,5.
V1 – ? H1 = 1,5 м, 2R = 0,8 м. V1 = π × 0,42 ? 1,5.
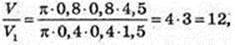
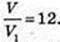
Відповідь: 12 бочок.
303.
V1 = 1,4 × 0,8; V = 2,4 × 3 × 4,2.
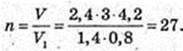 n = 27.
n = 27.
Відповідь: 27.
304 .
Припустимо, що V діам = V. Ціна його Ц = kV2. Розділимо цей діамант на 2 частини
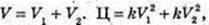 але
але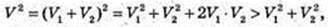 тому вигідніше продавати діамант цілим.
тому вигідніше продавати діамант цілим.
305.
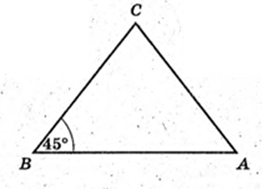
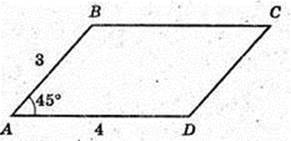
1) S – ? ΔABC: BA = 4 см, BC = 3 см, ∠ ABC = 45°.
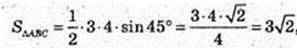
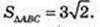
Відповідь: 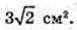
2)
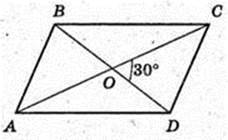
ABCD – паралелограм, AC = 12 см, BD = 10 см, ∠ DOC = 30°.
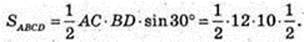
SABCD = 30 (см2).
Відповідь: 30 см2.
3)
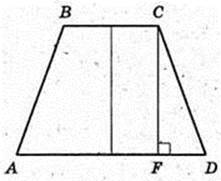
ABCD – трапеція, BC? AD, AB = CD = 10 см, BC = 4 см, AD = 16 см.
CF – ? FD – ?
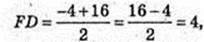 FD = 4.
FD = 4.
Δ CDF: ∠ F = 90°, CD = 10, 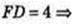
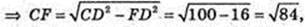
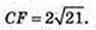
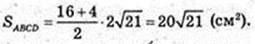
Відповідь: 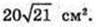
306.
1) 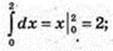
2) 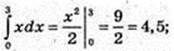
3) 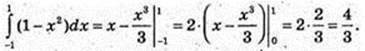
307.
A) S = 1 – x2,
Б) 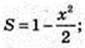
В) 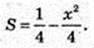
308.
1)
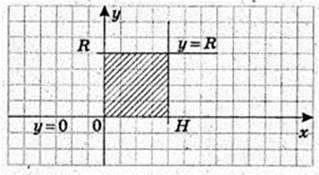
V – ? 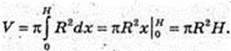
Відповідь: πR2Η.
2)
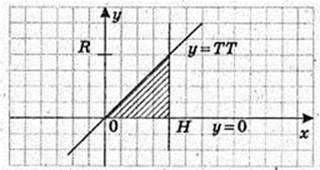
V – ? 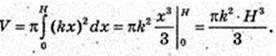
Відповідь: 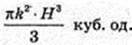
3)
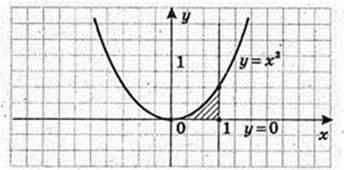
V-?
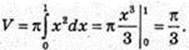
Відповідь: 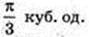
309.
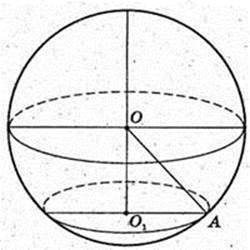
Куля (О, R). Переріз (O1, K1), OO1 = 4 см.
Sперер. = 9π см2 → πR12 = π × 9 → π × 9 → R1 = 3.
О1A = 3, OO1 =4 → ОА = 5, R = OA = 5.
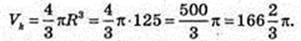
Відповідь: 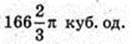
310.
V – ? R1 = 8 см, R2 = 4 см.
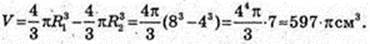
1 см3 = 0,000 001 м3. V= 597 × π × 10 -6 м3.
Mкулі = 597 × 3,7 × 10-6 × 73 × 102 = 597 × 73 × 3,7 × 10-4 ≈ 13,7 (кг).
Відповідь: ≈ 13,7 кг.
311.
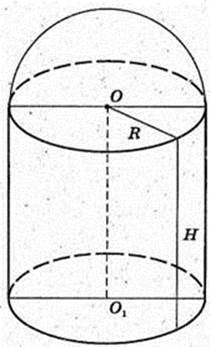
Півкулі і циліндр з тим самим радіусом.
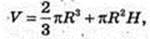
H – ? R = 14дм.1л = 1 куб. дм.
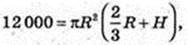
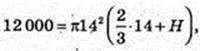 π = 3,14.
π = 3,14.
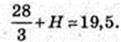 H ≈ 10,2 дм.
H ≈ 10,2 дм.
Відповідь: = 10,2 дм.
312.
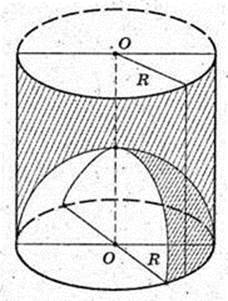
Vц = πR2H. 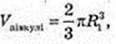 R1 = R = 2 см,
R1 = R = 2 см,
R × H = 64 → 2 × H = 64 → H = 32 см.
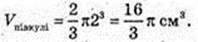 Vц = π × 22 × 32 = 128π см 3.
Vц = π × 22 × 32 = 128π см 3.
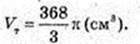
313.
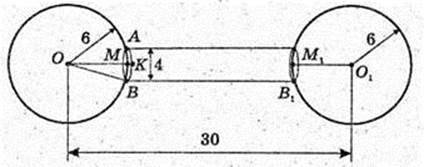
ΔOBM. OB = 6, BM = 2.
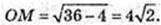
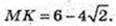
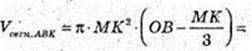
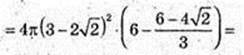
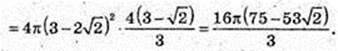
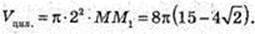
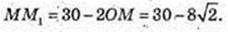
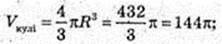
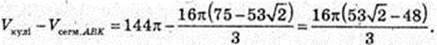
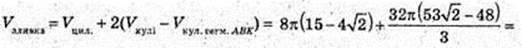
314.
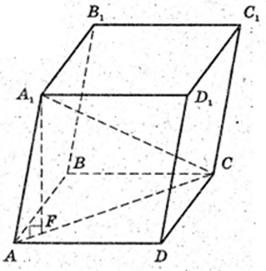
ABCDA1B1C1D1 – похилий паралелепіпед, основа – квадрат.
ABCD – квадрат. AB = а, AA1 = l, ∠A1AF = α,
A1F = H. V – ?
A1F = AA1 × sinα,
H = l × sin α, V = Sосн × H = а2 ×I sin α.
Відповідь: a2l sin α куб. од.
315.
ABCA1B1C1 – похила трикутна призма.
1)
AABC – правильний. AB = 4 см, AA1 = 6 см,
A1F + ABC, ∠ A1AF = 30°. V – ?
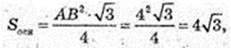
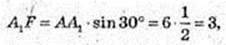
H = A1F = 3, 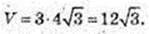
Відповідь: 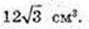
2)
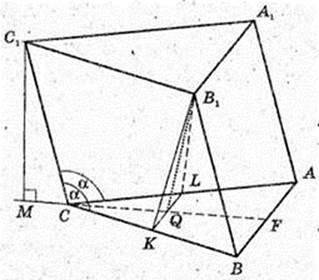
ABCA1B1C1 – похила трикутна призма.
Основа – трикутник ABC, ∠C = 90°,
CA = CB = α, CC1 = l, BB1 = CC1 = l, ∠CC1A = α,
C1CB = α. Vпр. – ? V = Sосн. × H, H -?
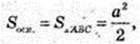 H – ?
H – ?
B1Q + ABC, H = B1Q. C1M + ABC, C1M = B1Q = Н,
B1K + CB, ∠B1BK = 180° – α.
B1K = B1B × sin(180° – α) = l × sin α,
B1L + CA.
За умовою, CB = CA, паралелограми BCCiB1 i ACC1A1 рівні,
Тому: якщо B1L + CA і B1K + СВ, то B1L = B1K,
AKB1L – рівнобедрений, у нього B1Q – висота, медіана.
За умовою ∠CC1B = ∠C1CA і B1Q + ABC,
Тоді т. Q належить бісектрисі кута ∠ACB,
Звідси CL = CK → B1K = B1L = I sin α.
KB = B1B cos(180°- α) = – l cos α →
→ CK = a – (-l cos α) = a + l cos α,
→ 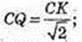
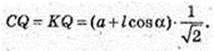
AB1QK: ∠Q = 90°, B1K = l sin α,
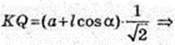
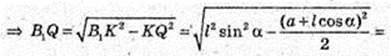
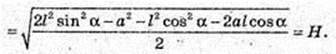
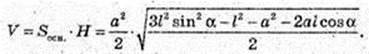
Відповідь: 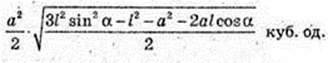
3)
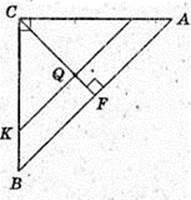
ABCA1B1C1 – похила трикутна призма.
Трикутник ABС – прямокутний, рівнобедрений,
∠ACB = 90°, CA.= CB = α, C1C = A1A = B1B = I, CF + AB,
C1F1 + A1B1, CF = h. Vпр. – ? Vпр. = Sосн. × H, Socн. – ? H – ?
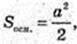 H – ? C1D + ABC1, C1D = H.
H – ? C1D + ABC1, C1D = H.
318.
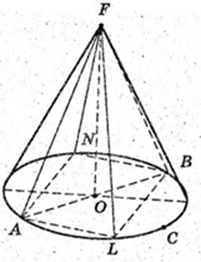
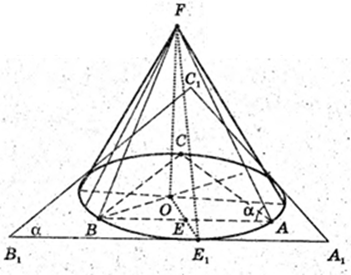
Дано прямий круговий конус.
V – ? FA = 6 см, FO + ABC, FO = H.
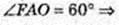
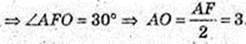
AO = 3, AO = R = 3.
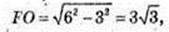
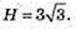
1) 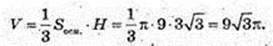
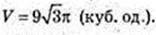
Відповідь: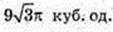
2) Rкулі – ? Vкулі = Vконуса 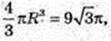
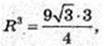
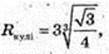
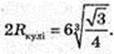
Відповідь: 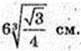
3)
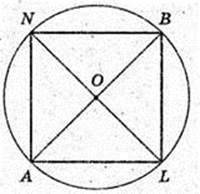
В конус вписана правильна чотирикутна піраміда
FANBL, V піраміди – ?
ANBL – квадрат, AO = 3, OL = 3,
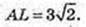
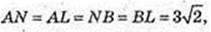
Soсн = AL2 = 9 × 2 = 18, 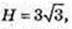
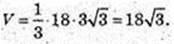
Відповідь: 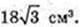
4)
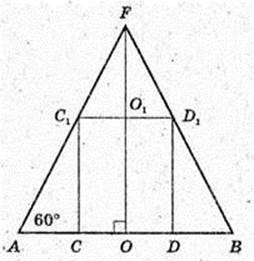
Прямий круговий конус. FA= 6 см, ∠FAO = 60°.
В конус вписано прямий круговий циліндр, OO1 = 3 см.
Vц – ? Vц = πr2, r – ? CO = r, r = C1O1.
За умовою ∠FAO = 60°, ∠AOF = 90°,
FA = 6 → AO = 3, 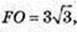
OO1 = 3. ΔFC1O1 ∞ ΔFAO,
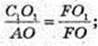
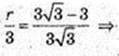
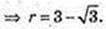
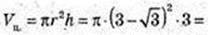
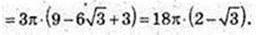
Відповідь: 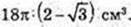
5)
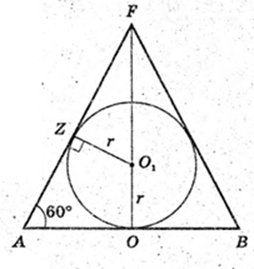
В косинус вписана куля. (О1, r). Vк – ?
AF = 6 см, AO = 3 см, 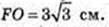
Точка Z – точка дотику кулі і конуса.
O1O = r, O1Z = r. r – ? AO = AZ = 3 → FZ = 3.
ZO1 + AF,
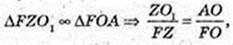
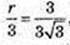
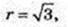
Відповідь: 
6)
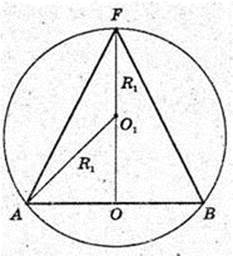
Куля (О1, R1) oписана навколо конуса.
Vк – ? R1 – ? 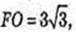 FO1 = R1,
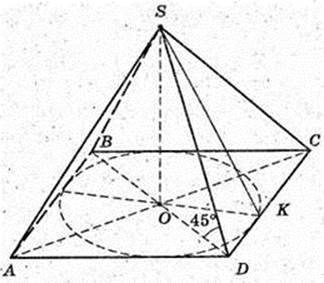
FO1 = R1,
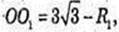 AO = 3, R1 = x.
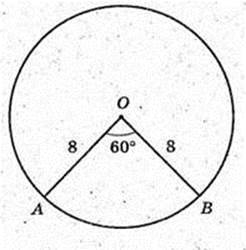
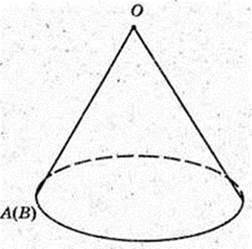
AO = 3, R1 = x.
ΔAO1О: ∠O1OA = 90°;
AO1 = х, 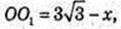 AO = 3.
AO = 3.
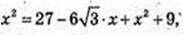
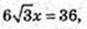
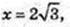
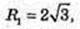
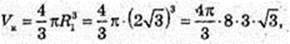
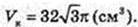
Відповідь: 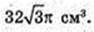
319.
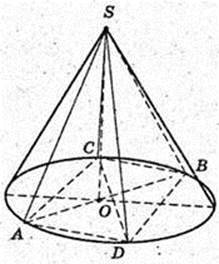
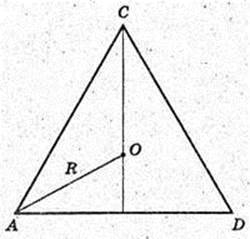
Дано прямий круговий конус, твірна SA = І, ∠ASB = α.
Переріз ASB – осьовий переріз.
1) Vк – ?
ΔSAO: ∠SOA = 90°, 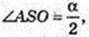 AS = l,
AS = l,
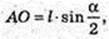
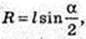
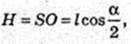
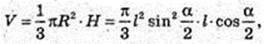
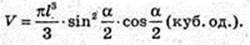
Відповідь: 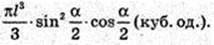
2) куля (O1, R).
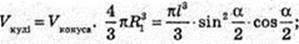
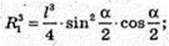
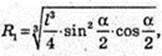
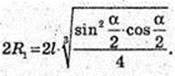
Відповідь: 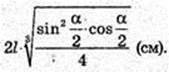
3)
В конус вписана трикутна піраміда, правильна піраміда SACD.
Vпір – ? 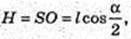
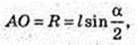
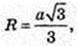 a = AC.
a = AC.
AC – ? 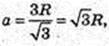
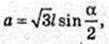
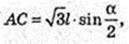
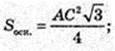
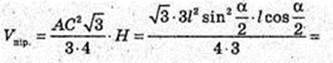
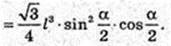
Відповідь: 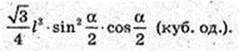
4)
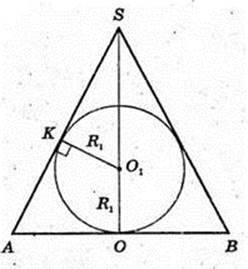
В конус вписана куля (O1, R1). Vкулі -?
Точка K – точка дотику конуса і кулі.
ΔASB – осьовий переріз. OK1 + AS, OK1 = R1
R1 -?
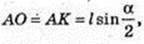 SA = l,
SA = l, 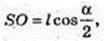
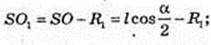
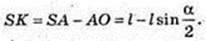
ΔSO1K ∞ ΔSAO. R1 = x, 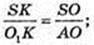
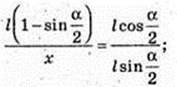
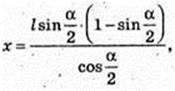
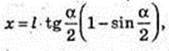
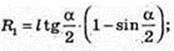
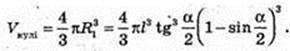
Відповідь: 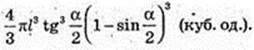
5)
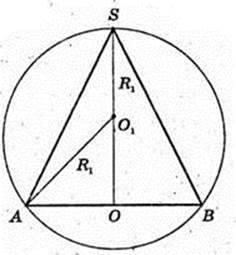
Куля (О1, R1) описана навколо конуса. V кулi – ?
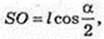
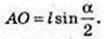 SO1 = R1 = x – ?
SO1 = R1 = x – ?
ΔAO1O: ∠O = 90°, 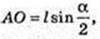
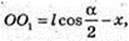 AO1 = х, x – ?
AO1 = х, x – ?
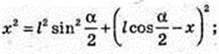
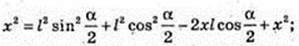
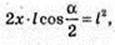
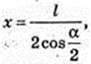
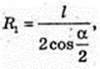
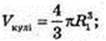
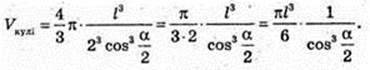
Відповідь: 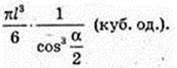
320.
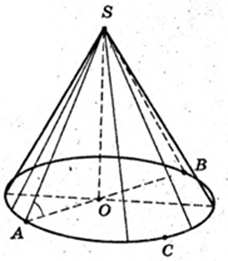
Конус. 
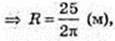
SA = 5 м, SO + ABC,
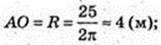
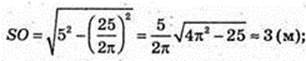
H = SO = 3;
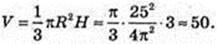
V = 50 (м3). M = 100 т. n = 100 : 3 = 33,3 (ходок).
Відповідь: 34 ходки.
321.
Косинус, твірна SA = 0,2 км, ∠SAO = 46°, V – ? M – ?
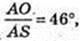 R =AO=AS × cos 46° = 0,2 cos 46°; R = 0,2 × cos 46° = 0,2 × 0,68,
R =AO=AS × cos 46° = 0,2 cos 46°; R = 0,2 × cos 46° = 0,2 × 0,68,
R = 0,136 (км); H = SO = AS × sin 46° = 0,2 × 0,72 = 0,144, H = 0,144 (км);
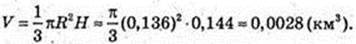
V= 2800 м3 × 1000 = 28 × 106 м3. M = 56 × 106 т.
Відповідь: 56 млн. м.
322.
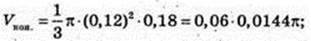
Vцил. = Vкон. = π × 0,052. H = 0,06 × 0,014π.
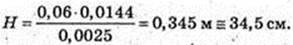
323.
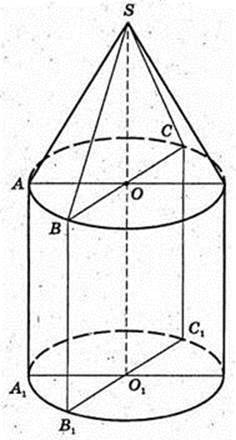
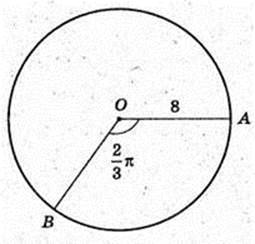
Циліндр і конус, основа – спільна. Rц = Rк =BO.
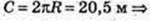
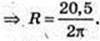
HЦ = SO = 4 м. Hц = OO1 = 2,2 м.
V – ? M – ? ρ = 0,03 г/м3.
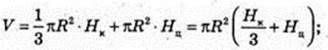
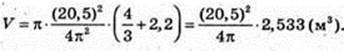
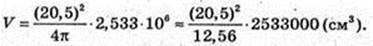
M = (20,5)2 × 201672 × 0,03 = 2542580 г = 2542,58 кг ≈ 2,5 т.
Відповідь: ≈ 2,5 т.
324.
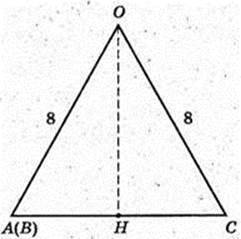
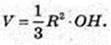
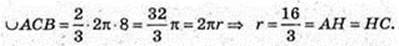
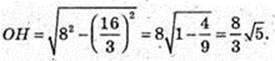
ΔAΟΗ: 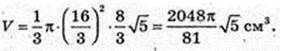
325.
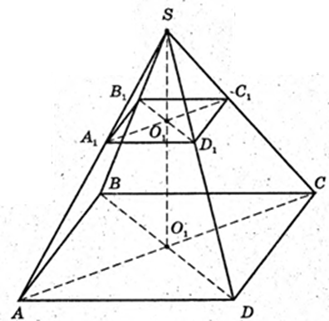
SABCD – правильна чотирикутна піраміда.
AB = BC = CD =AD = 8 см. SA = SB = SC = SD = 9 см.
1) V пір. – ? 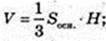 SOCH = AB2 = 82 = 64;
SOCH = AB2 = 82 = 64;
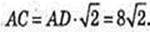 SO + ABC, SO = H – ?
SO + ABC, SO = H – ?
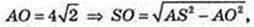
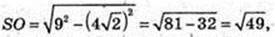
SO = 7.
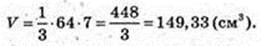
Відповідь: 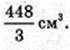
2) V кулі = Vпір., Rкулі – ?
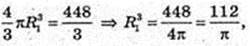
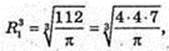
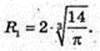
Відповідь: 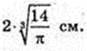
3)
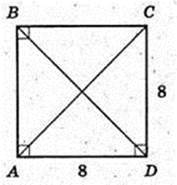
Переріз A1B1CD1 з центром в точці O1,
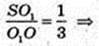
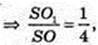
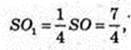
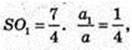
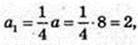
A1 = 2. 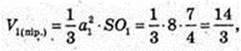
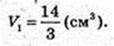
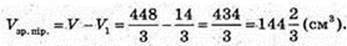
Відповідь: 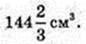
326.
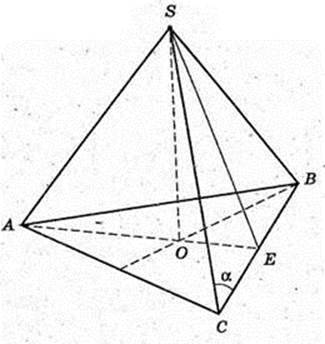
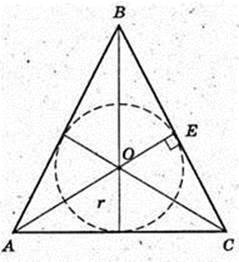
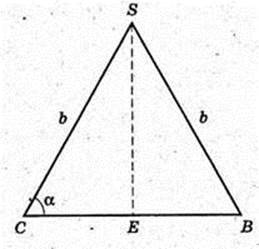
SABC – правильна трикутна піраміда SA = SB = SC = b. ∠SCB = α.
1) Vпір. – ? 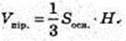
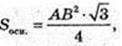
AB -? AB = BC = AC = а – ? H = SO -? ΔSCE, SE + CB.
В ΔCSB SC = SB, CE = EB.
CE = b cos α, CB = 2b cos α, a = 2b cos α. SE = b sin α.
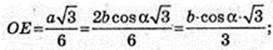
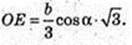
ΔSOE: ∠O = 90°, SO2 = SE2 – OE2;
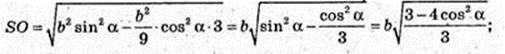
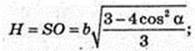
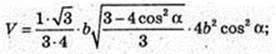
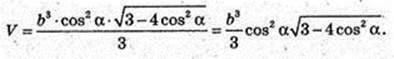
Відповідь: 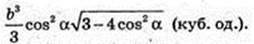
2)
В піраміду вписано прямий круговий конус. Vкoн – ?
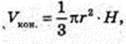
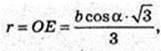
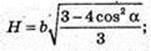
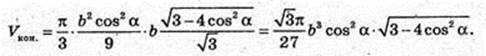
Відповідь: 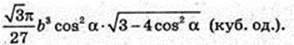
3)
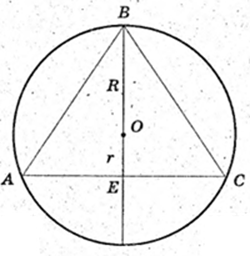
Знайти відношення об’єму вписаного в піраміду прямого кругового конуса до об’єму описаного навколо цієї піраміди прямого кругового конуса.
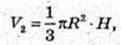
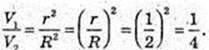
Відповідь: 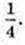
4)
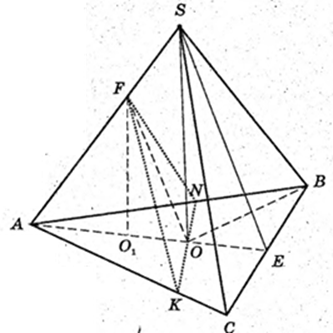
Переріз KFM? CSB, KF? CS, FN? SB, KN? CB. VANFK -?
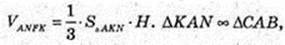
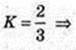
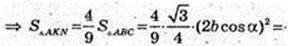
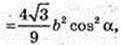
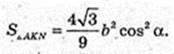
H1 – ? 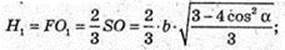
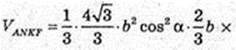
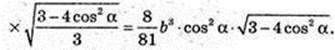
Відповідь: 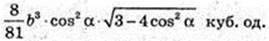
327.
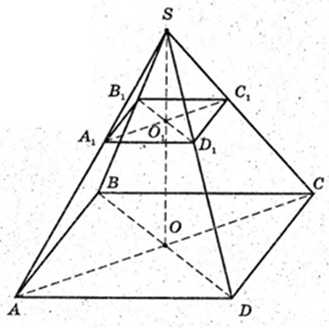
Піраміда SABCD, основа – прямокутник ABCD,
AB = 6 см, AB = 8 см, SA = SB = SC = SD = 13 см.
1) V пір. – ? 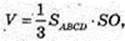
SO = H, SO + ABC. ABCD – прямокутник.
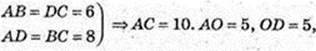
SD = 13. ΔOSD: ∠O = 90°, OD = 5, SD = 13 → SO = 12, H = 12.
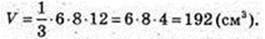
Відповідь: 192 см3.
2) V пp. = V пip. H – ?
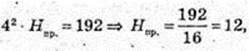
H пp. = 12 .
Відповідь: 12 см.
3) ABCDA1B1C1D1 – зрізана піраміда A1B1C1 ? АBС,
OO1 = 9 → SO1 = 12 – 9 = 3, SO 1 = 3, SO1: SO = 3 : 12 = 1 : 4.
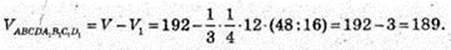
VABCDA1B1C1D1 = 189 куб. од.
4) 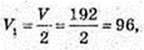
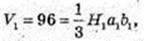
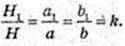
H 1 = H × k, a1 = а × k,
B1 = bk, 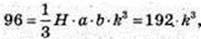
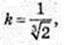
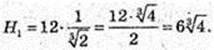
Відповідь: 
328.
ΔABC – рівносторонній. 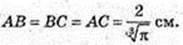
1)
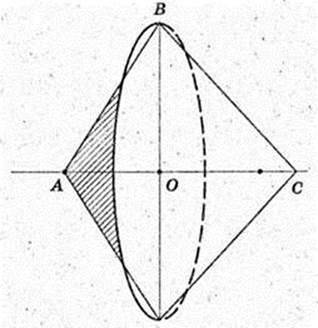
Трикутник обертається навколо сторони АС. Утворюється 2 конуса,
У них спільна основа з радіусом R = OB і висотою H = ОС.
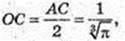
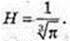
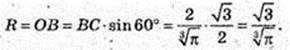
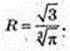
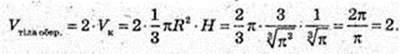 V = 2 CM3.
V = 2 CM3.
Відповідь: 2 см3.
2)
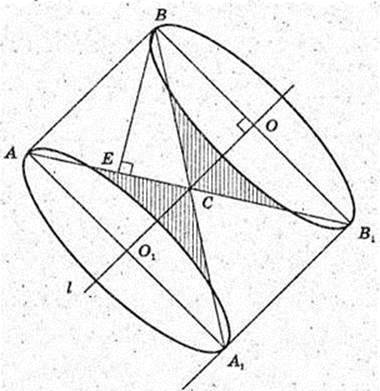
ΔАВС, АB = ВС = АС = 6 см.
Трикутник обертається навколо лінії l, де l? AB.
Утворюється два конуса,
Однакові, R = OB, H = ОС.
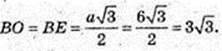
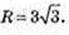
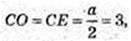 H = 3.
H = 3.
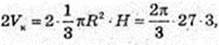 2Vк = 54π,
2Vк = 54π,
Утворився циліндр з висотою AB і радіусом основи OB = EB, AB = 6,
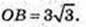
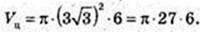
Vтіла об. = Vц – 2Vк = 27 × 6π – 54π = 54 × 2π = 108π.
Відповідь: 108π куб. од.
3) ABCD – ромб. 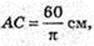
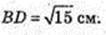
Ромб обертається навколо більшої діагоналі.
Утворилися два конуса, у них спільна основа з радіусом
R = OB і висотою AO = CO = H.
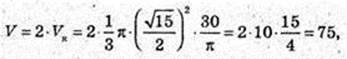 V= 75 см3.
V= 75 см3.
Відповідь: 75 см3.
4)
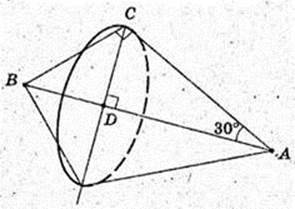
Трикутник ABC, ∠C = 90°, BC = 6 см, ∠CAB = 30° → AВ = 12.
Трикутник обертається навколо гіпотенузи BA,
Утворюються два конуса, у них спільна основа з радіусом
R = CD і висоти H1 = AD і H1 = ВD.
V тіла обер. = V 1 + V – ?
BC = 6, BD = 3, 
CD2 = BD × AD, 27 = 3 × AD, AD = 9.
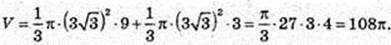
Відповідь: 108π см3.
5)
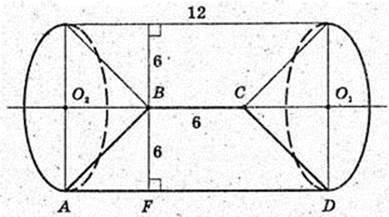
Трапеція ABCD, BC? AD, обертається навколо BC,
BC < AD, BC = 6 см, AD = 12 см, BF = 6 см. BF + AD.
Відповідь: 360π.
6)
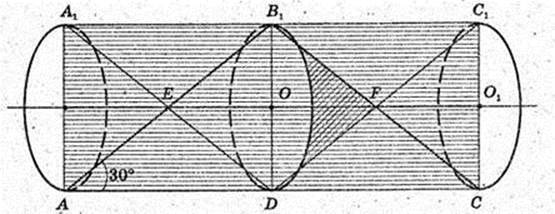
Рівнобедрений трикутник ABC, AB = BC, AC = 12 см,
∠ABC = 120°, EF – середня лінія, EF? АС.
Трикутник обертається навколо середньої лінії EF,
Утворюються циліндр і 4 конуса, у них радіус основи
R = OB, висота H = EO. OB – ? OE – ?
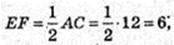 EO = 3.
EO = 3. 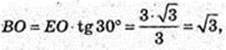
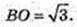
Утворився циліндр з висотою OO1 = 6 і радіусом основи
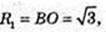
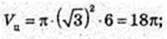
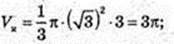
Vтіла об. = 2 × (Vц – Vκ) = 2(18π-3π) = 30π.
Відповідь: 30πсм3.
329.
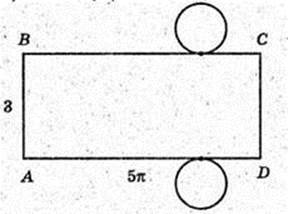
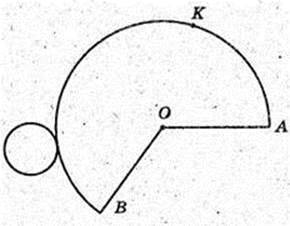
1) ABCD – прямокутник, AB = 3 см, AD = 2πR = 2R × π = 5π см,
2) OA = см; AKB = 2π × 2 = 4π.
330.
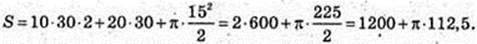
Відповідь: (1200 + 112,5 × π) кв. од.
331.
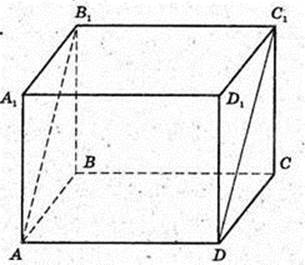
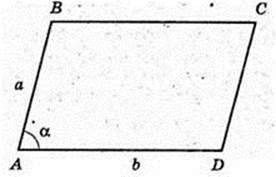
ABCDA1B1C1D1 – прямий паралелепіпед.
ABCD – паралелограм, AB = a, BC = b, b > a.
∠BAD = α, AA1 = І.
1) Sб. пов. -?
S б. пов. = 2 × (a + b) × l.
Відповідь: 2 × (a + b) × l.
2) Sп. пов – ?
Sп. пов = 2(а + b) × l + 2 × а × b × sin α.
Відповідь: 2((а + b)l + аb sin α).
3) S AB1C1D -?
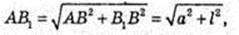
AD = b. 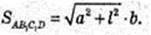
Відповідь: 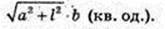
332 .
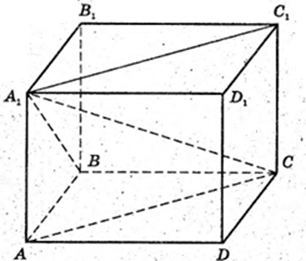
ABCDA1B1C1D1 – правильна чотирикутна призма.
1) 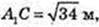 A1B = 5 м. Sп. п. – ?
A1B = 5 м. Sп. п. – ?
ΔA1CB: ∠B = 90°, 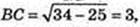
BC = 3. AB = BC = CD = AD = 3; a = AB = 3.
ΔA1AB: ∠A1AB = 90°; A1B = 5, AB = 3 → A1A = 4, H = A1A = 4.
2) Sп. п. = 2Sосн. + 4SABB1A1 = 2 × 32 + 4 × 3 × 4 = 2
Sп. п. = 2 × 9 + 48 = 18 + 48 = 66, Sп. п. =66 (м2).
Відповідь: 66 м2.
3) Sп. п. -?
AB = 3 м. A1B = 5м. Sn. п. =66 м2.
4) Sп. п. -?
SAA1C1C = S, 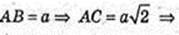
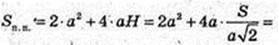
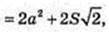
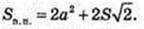
Відповідь: 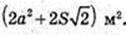
333.
ABCA1B1C1 – пряма призма.
1)
ΔABC – правильний.
AB = 12 см, ∠ B1AB = 60° → AB = 6 см,
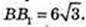 Sп. п. – ?
Sп. п. – ?
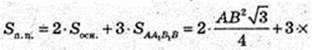
Відповідь:
2)
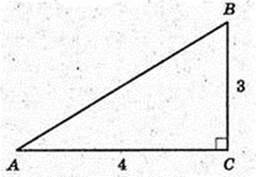
Δ ABC: ∠ C = 90°, BC = 3 см, AC = 4 см → AB = 5 см.
SA1B1B = 10 см 2, 10 = 5 × AA1, H = AA1 = 2 (см). Sп. п. – ?
Відповідь: 57 см2.
334.
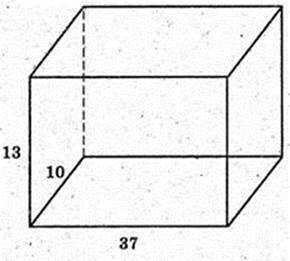
S б. = 2 × (13 × 10 + 13 × 37) = 26 × 47 (м2).
Кількість розчину M = 20 × 26 × 47 кг = 24,44 кг.
335 .
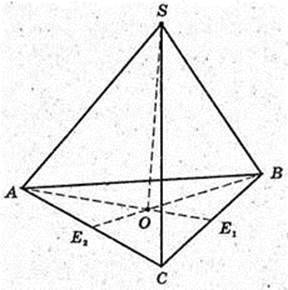
SABC – правильна трикутна піраміда.
AS = BS = CS = 12 см.
1)
Sп. п. – ? SO =H. ∠ ASO = 30°.
З умови маємо 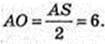 AO = 6,
AO = 6,
ΔABC: 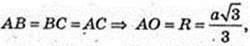
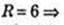
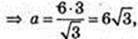
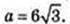
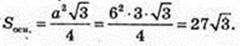
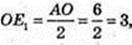 OE1 = 3.
OE1 = 3.
Відповідь: 
2)
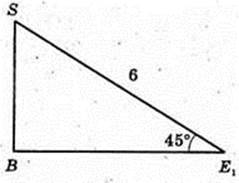
Sп. п. -? SE1 = 6 см, ∠ SE1A = 45°.
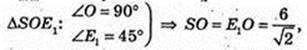
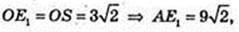
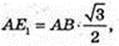
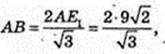
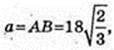
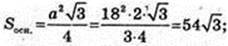
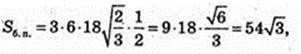
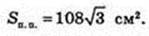
Відповідь: 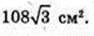
3)
Δ ABC: AB = BC = AC = b. Sп. п. – ?
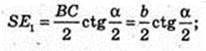
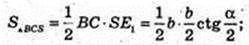
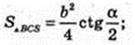
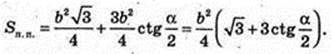
Відповідь: 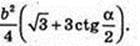
4)
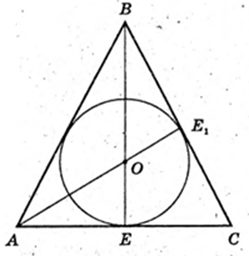
∠SAE1 = α, OE = r. Sп. п. – ?
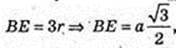
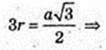
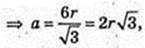
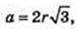
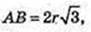
AE1 = BE = 3r.
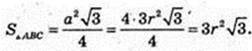
ΔSAO: ∠O = 90°, ∠SAO = α,
AO = 2r → SO=AO × tg α, SO = 2r tg α.
ΔSOЕ1: ∠O = 90°, OE1 = r, 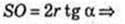
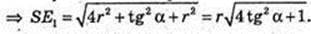
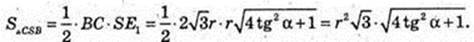
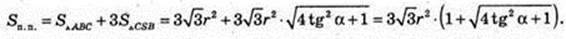
Відповідь: 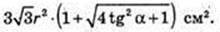
5) ΔABC – правильний, AB = BC = AC = a.
Vnip = V. Sп. п. – ?
Sп. п. = Socн. + 3SΔBCS, 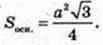 SЕ1 – ? SO – ?
SЕ1 – ? SO – ?
ΔABC: AB = a, 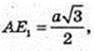
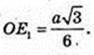
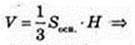
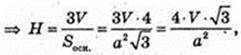

ΔSOЕ1: 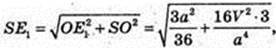
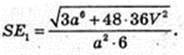
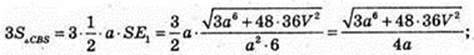

Відповідь: 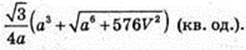
6) Vпір. = V, ∠ASO = α → 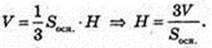
Позначимо AB = a, тоді 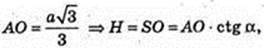
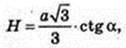
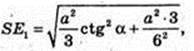
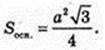
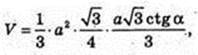
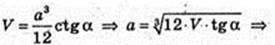
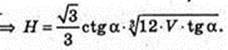
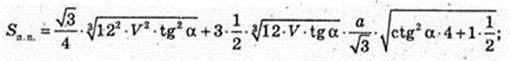
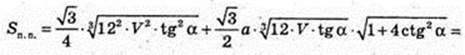
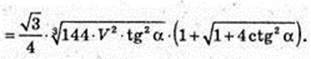
336.
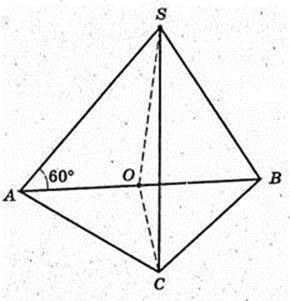
SABC – трикутна піраміда.
1)
ΔABC – прямокутний рівнобедрений, ∠ACB = 90°, АВ = 5 см.
Всі бічні ребра SA, SB, SC нахилені до площини основи під кутом 60°,
∠SAO = ∠SBO = SCO = 60° → SO = Н, де т. Н – центр кола, описаного навколо ΔABC, т. О? АВ, AO = ОВ = ОС = R. АВ = 5, АО = 2,5, R = 2,5. Sб. піраміди – ?
ΔABC: ∠C = 90°, АС = ВС, 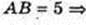
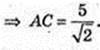
ΔASO: ∠O = 90°, 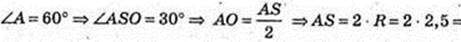
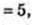
AS = 5 → BS = 5.
ΔASB: 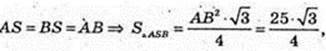
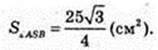
ΔASC: SA = SC = 5,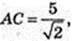
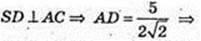
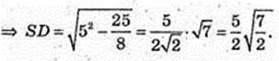
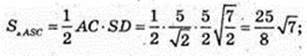
Відповідь: 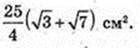
2)
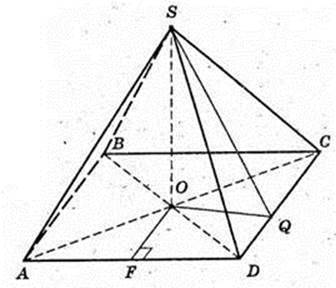
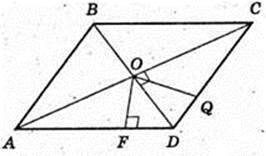
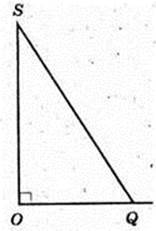
Піраміда SABCD, ABCD – ромб,
BD = 6 м, AC = 8 м, SO = H, AC  BD = 0. SO + ABC. SO = 1 м. Sб. п. – ?
BD = 0. SO + ABC. SO = 1 м. Sб. п. – ?
Δ DOC: ∠O = 90°, OC = 4, OD = 3 → DC = 5 = AD. OQ + DC, DC – ?
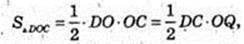
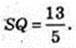
DO × OC = DC × OQ, 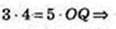
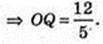
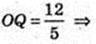
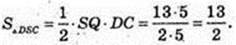
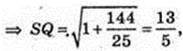
 Sб. п. = 26M2.
Sб. п. = 26M2.
Відповідь : 26 м2.
337.
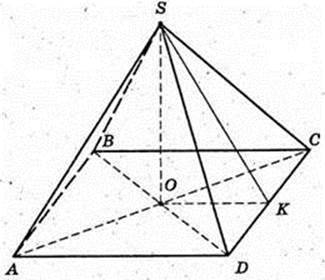
 CD = 1,8 (за умовою).
CD = 1,8 (за умовою).
ΔOSK: 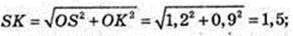
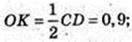
OS = 1,2 (за умовою). Sб. = 2 × 1,8 ×1,5 = 5,4.
Площа заліза: Sб. +10 % × Sб. = 5,4 + 0,54 = 5,94 ≈ 6 м.
338.
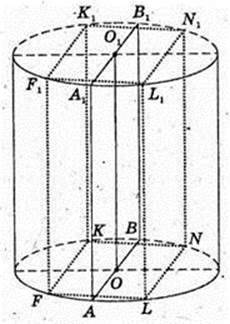
Циліндр прямий круговий. AA1B1B – осьовий переріз.
SAA1B1B =8 см2, АО = R = 2 cм.
1) S б. п. – ? S б. п. = 2πR × H – ?
SAA1B1B = AA1 × AB = H × 2R = 2RH = 8. S б. п. = 8π.
Відповідь: 8π см2.
2) S п. п. – ? Sп. п. = S б. п. + 2Sосн. – ?
Sосн. = πR2 = π × 4 = 4π, S п. п. = 8π + 8π = 16π.
Відповідь: 16π см2.
3)
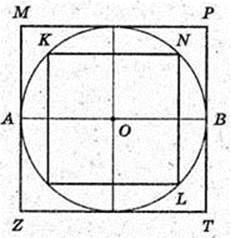
В циліндр вписана правильна чотирикутна призма з основою FKNL – квадратом. Sп. пр.- ? Н = FF1 – ?
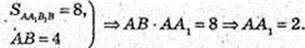
Н = AA1 = FF1 = 2.
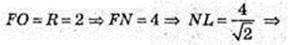
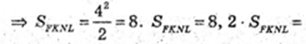
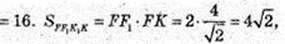
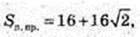
Біля даного циліндра описана правильна чотирикутна призма, її основа – квадрат ZMPT. сторона квадрата ZT = 2R = 4, Sосн. = 42 = 16, 2Sосн. = 32.
Sб. пр.= 4 × АА1 × ZT = 4 × 2 × 4 = 32. S п. пр. = 32 + 32 = 64.
Відповідь: 64 см2.
339.
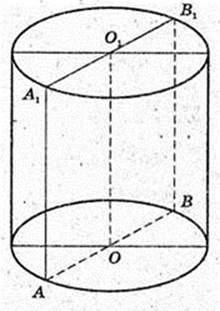
Прямий круговий циліндр. AA1B1B – осьовий переріз,
SAA1B1B = p. Vп = 3.
1) Sп, п, – ?
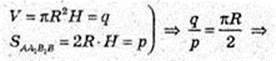
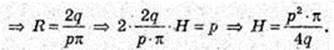
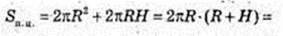
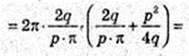
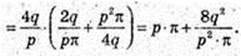
Відповідь: 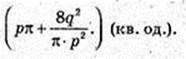
2) 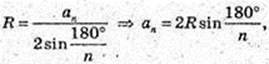
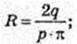
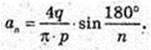
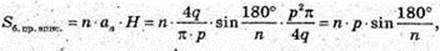
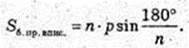
Відповідь: 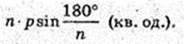
340.
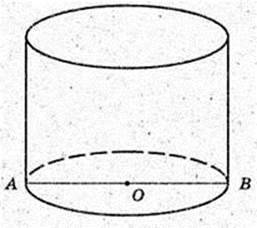
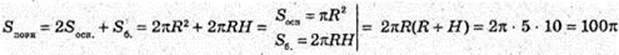
Sматер. = 106 – 102 × π + 0,1 × 108 × π = 107 × π × (10 + 1) = 11π × 107 см 2 =
= 1,1π × 104 M2 = 11 000π м 2.
341.
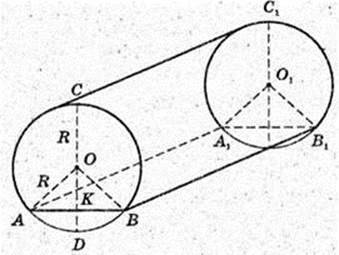
S = 2πR × H.
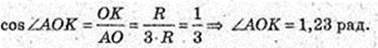
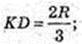
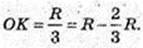
∠ AOBC = 2π – 1,23); 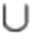 ACB = 2(π – 1,23)R.
ACB = 2(π – 1,23)R.
Sб. = (2π – 2,26) RH = 3,82RH м – обсяг роботи.
Кількість краски M = 3,82ρHR кг, де ρ – кг/м2 – кількість краски на 1 м2.
342.
V=πR2 × H =104 см3, 
S = πR2 + 2πRH = πR(R + 2Н) = 2091 см2.
Кількість матеріалу: 2091 + 209 = = 2300 см2 = 0,23м2.
343.
Прямий круговий конус.
Sосн.= S. SO + ABC, SO = H. OA = R, ∠ FAO = α.
1) Sб. к. – ?
Sб. к. = πRl, l = FA.
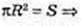
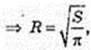
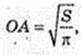
L – ? 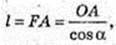
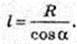
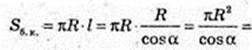
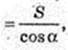
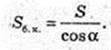
Відповідь: 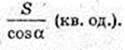
2) 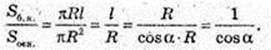
Відповідь: 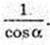
3)
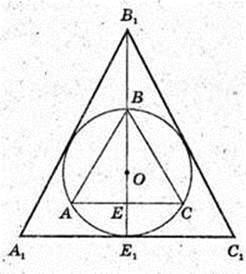
В конус вписана правильна n-кутна піраміда і описана правильна n-кутна піраміда. Знайти відношення площ бічних поверхонь цих пірамід.
344.
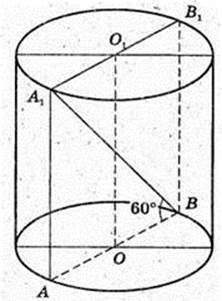
Дано прямий круговий циліндр, АА1В1В – осьовий переріз.
А1В = 16 см. ∠А1ВА = 60°. ОО1 = Н.
1) Sп. п. – ? АВ – ? АА1 = H – ?
Δ A1AB: ∠ А = 90°, АВ = 60°, А1В = 16.
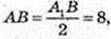
АВ = 8 → В = 4. Sосн. = πR2 = 16π. 2Sосн. = 32π.
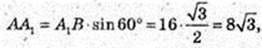
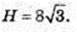
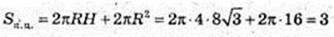
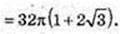
Відповідь: 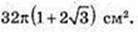
2) Sб. к. – ? Hк. = Hц. Sосн. к. = Sосн. ц. Sб. к. = πRl, l – ?
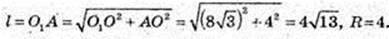
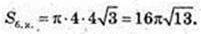
Відповідь: 
345.
1) Sповн. пір. = Sосн. + Sб.
ΔOSD: 2OS2 = SD2, OS2 = 18.
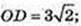
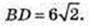
ΔABD: 2a2 = BD2, a = 6. ΔADS – правильний.
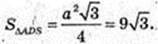 S осн. = a2 = 36;
S осн. = a2 = 36;
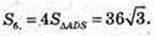
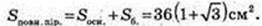
2) 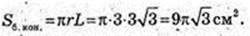
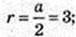
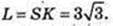
3) 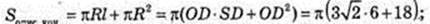
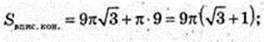
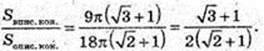
346.
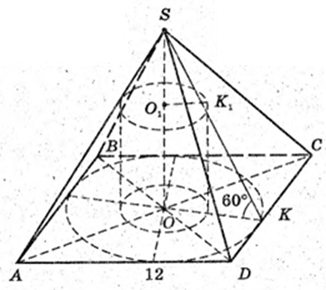
Sповна пірам. = Sосн. + S б.. Sосн. = 144.
 S повна пірам. = 144 + 288 = 432 дм2.
S повна пірам. = 144 + 288 = 432 дм2.
1) S б. = 288 дм2.
2) Sкуба = 6а2 = 432 =
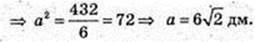
3) Sкон = πR2 + πRL = 36π + 72π = 108π дм2.
R = 6, L = SK = 12.
4)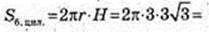
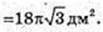
AOSK: 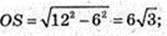
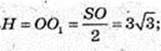
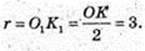
347.
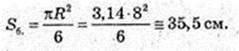
348.
S б. = πRL. ΔSBO. 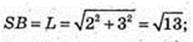
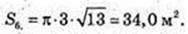
Sматер. = 34 + 3,4 = 37,4 м2. S1 листа = 0,98 м2.
Кількість листів: 
349.
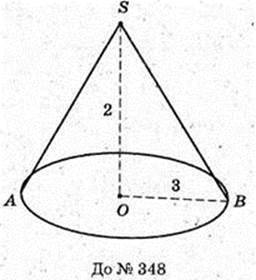
S = π(r2 + L(R + r)). ΔBB1K.
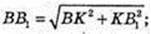
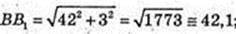
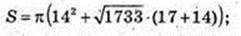
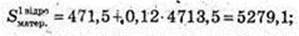
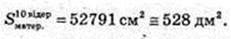
350.
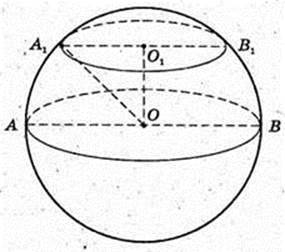
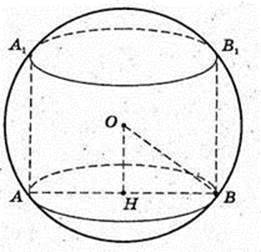
1) OO1 = 4 (з умови), CO1 = 18 → 2πr = 18;
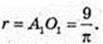
ΔA1O1O: 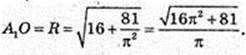
Площа поверхні кулі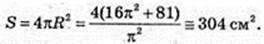
2)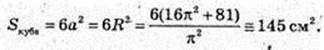
3) ОH = ВH (з умови). ΔОВH:
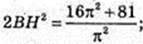
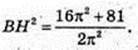
4) S опис. цил. = 2πR2 + 2πR × 2R = 6πR2.
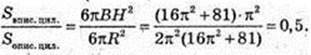
351.
1) Радіус сфери, вписаної в куб з ребром а, дорівнює 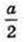
І поверхня сфери 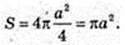
2) Радіус сфери, вписаної в циліндр з радіусом основи R і висотою 2R,
Дорівнює R і поверхня сфери S = 4πR2.
3)
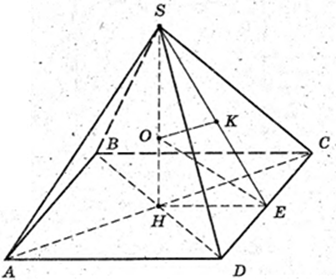
Розглянемо ΔSHE, ОЕ – бісектриса
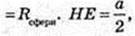 SH = h,
SH = h,
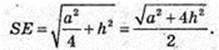
Властивість бісектриси: 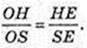
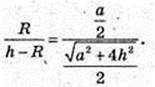
Властивість пропорції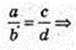
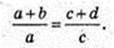
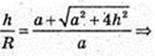
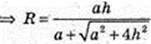
І поверхня сфери 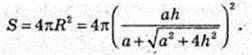
352.
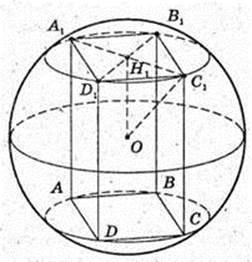
1) Нехай радіус кулі, описаної навколо куба ОС1 = Е,
А ребро куба АВ = ВС = … АА 1 = А,
Тоді 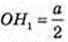 і
і 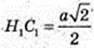 із Δ OH1C1:
із Δ OH1C1:
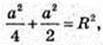
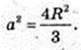
Радіус кулі, вписаної в куб, дорівнює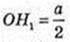
І поверхня цієї кулі
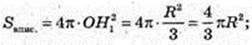
S опис. = 4πR2; 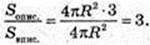
2)
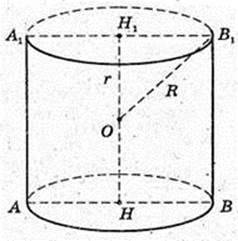
Нехай АА1 = АВ = а,
Тоді 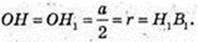
Із ΔОH1B1: 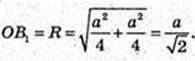
Sкулі опис. = 4πR2 = 2π2; Sкулі опис.= 4πr2 = πа2,
353.
AO = OB = 2 см (з умови).
SAA1B1B = AB × AA1 = 4AA1 = 64 см2 → АА1 = 16 см.
Циліндр:
S Пов. = 2π × АО2 + 2π × АО × АА1 = 2π × АО(АО +АА1) = 4π × 18 = 72 см2. Півкуля. Sпов. = 2π × АО2 + π × АО2 = 3π × AO2 = 12π см2.
Куб із півкулі:
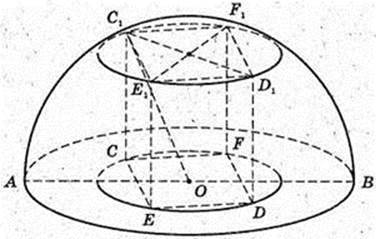
Нехай ребро куба СЕ = DE = … = СС1 = а,
Тоді з ΔCDE 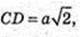
З ΔОСС1 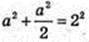 (OC1 – радіус півкулі, ОС1 = 2).
(OC1 – радіус півкулі, ОС1 = 2).
Звідси 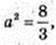 а поверхня куба
а поверхня куба 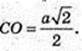
Sкулі = 6 × а2 = 16см2. Це буде найбільший куб, який можна вирізати із півкулі.
354.
Куб об’ємом V має площу поверхні
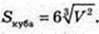 V = а3,
V = а3, 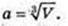
Куля об’ємом V має площу поверхні
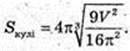
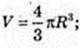
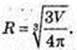
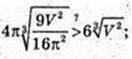
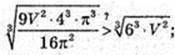
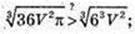
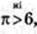
Тобто Sкуба. >S кулі..
Куб охолоне швидше, ніж куля.
355.
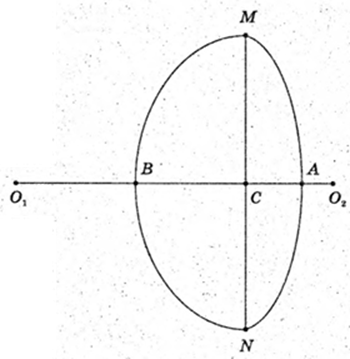
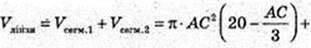
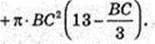
Розглянемо ΔO1MC і ΔO2МС.
2О2 – OC2 = 132 – (21 – O1C) → O1C = 16 і O2C = 5(O1C + O2C = 21).
Тоді AС = 4(AС = O2C – О2А = 5 – 1 = 4) і BС=BO2 – СО2 =13 – 5 = 8.