Одночлен. Стандартний вигляд одночлена
Урок № 26
Тема. Одночлен. Стандартний вигляд одночлена
Мета: домогтися свідомого розуміння змісту основних понять уроку (одночлен; одночлен стандартного вигляду, коефіцієнт одночлена стандартного вигляду; степінь одночлена); вдосконалювати вміння виконувати перетворення степенів.
Тип уроку: засвоєння знань учнів.
Хід уроку
I. Перевірка домашнього завдання
@ Щоб перевірити корекцію самостійної роботи, збираємо зошити на перевірку та за необхідності висвітлюємо найскладніші завдання (з погляду учнів) попередньої самостійної
II. Робота з випереджальним домашнім завданням
Учні виконують завдання самостійно, використовуючи підручник та свої записи.
Нове поняття | Тлумачення в підручнику | Приклад, порівняння щодо змісту | Корекція |
Після виконання завдання працюємо над корекцією.
III. Засвоєння нових знань
Отже, основними новими поняттями, які розглянуто у відповідному пункті підручника, є:
1) одночлен;
2) одночлен стандартного вигляду;
(Що таке “стандарт” – знайти в тлумачному словнику.)
3) коефіцієнт одночлена,
(Що таке “коефіцієнт” – знайти в тлумачному словнику.)
4) степінь одночлена.
(Чи є тотожними поняття “степінь числа” та “степінь одночлена”?)
Зміст виділених понять учні знаходять самостійно й усвідомлюють, знайшовши числові порівняння.
IV. Закріплення знань. Формування вмінь, удосконалення навичок
Виконання усних вправ
1. Чи є одночленом вираз:
1) 3,4х2у; 2) -0,7ху2; 3) а • (-8); 4) х2 + х; 5) х2х; 6) –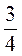 
M3nm2; 7) а – b;
8) 2(х + у)2; 9) -0,3ху2; 10) с10; 11) – m; 12) 0,6?
@ Вимагаємо від учнів пояснень, закріплюємо знання означення одночлена.
2. Чи записано у стандартному вигляді одночлен:
1) 6ху; 2) -2aba; 3) 0,5m •2n; 4) – bса; 5) – х3у3; 6) 5р3р2 ?
@ З метою виховання математичної культури звертаємо увагу на те, що в одночлені стандартного вигляду степені з різними основами записуємо в алфавітному порядку їх основ.
3. Назвіть коефіцієнт одночлена й визначте його степінь:
1) 3х5; 2) -7ху; 3) 6х2 •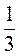 
У; 4) 17; 5) – а5; 6) у.
Виконання письмових вправ
1. Зведіть одночлен до стандартного вигляду, вкажіть його коефіцієнт та степінь:
1) 8х3 • хх5;
2) 3а • 0,5b • 4с;
3) 3а • (-2ас);
4) -2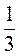M2 • 6mn3;
5) -2х3 • 0,1х3у • (-5у);
6) p • (-q) • p20.
2. Складіть усі можливі одночлени стандартного вигляду з коефіцієнтом 5, що містять дві змінні х та у так, щоб степінь кожного одночлена дорівнював: 1) трьом; 2) чотирьом.
3. Знайдіть значення одночлена:
1) 4х2, якщо х = -3;
2) -32а2b3, якщо а =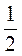 
, b = – 1;
3) 
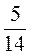Х2у, якщо х = 7, у = 0,6;
4) 0,6аbс2, а = 1,2, b = -5, с = 3.
4. Чому дорівнює об’єм прямокутного паралелепіпеда, ширина якого а см, довжина у 2 рази більша за ширину, а висота у 2 рази більша від довжини? Складіть і запишіть вираз до цієї задачі. Як ви назвете здобутий вираз? Обчисліть його значення при а = 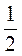(м).
5. Обчисліть значення виразу: 1)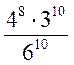 
; 2)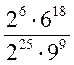 
.
V. Підсумки уроку. Рефлексія
“Німий диктант”
На дошці записано одночлен стандартного вигляду та одночлен, що не є одночленом стандартного вигляду: 1) 7a3bc4; 2) 7а3bс • с3.
Учитель почергово вказує на відповідні елементи запису, а учні повинні записати математичну назву загального поняття, що подається цим записом.
Наприклад:
– учитель указує на вираз 2) – учні записують “одночлен”;
– учитель вказує на вираз 1) – учні повинні записати “одночлен стандартного вигляду” тощо.
VI. Домашнє завдання
№ 1. Зведіть одночлен до стандартного вигляду, вкажіть його коефіцієнт та степінь:
1) 8у2 • у3 • у;
2) 7 • х • 0,1у2z;
3) 5b • (-3аb);
4) -2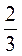
M4 • 9mn3;
5) -3a2 • 0,2ab4 • (-10b);
6) х3 • (-у)3 • х.
№ 2. Знайдіть значення одночлена:
1) 3х3, якщо х = -3; 2) 0,8m2nр, якщо m = -0,2, n = 3, р = 5.
№ 3. Випереджальне домашнє завдання. Знайдіть у підручнику приклад на множення одночленів та піднесення одночлена до степеня. Прочитайте та знайдіть (виділить) знайомі та незнайомі поняття, властивості, алгоритми. Які саме властивості дій над числами є основою розв’язання прикладів (випишіть їх назву).
(1 votes, average: 5.00 out of 5)
Loading...