Головна ⇒ 📌Довідник з геометрії ⇒ Означення синуса, косинуса, тангенса, котангенса для будьякого кута від 0° до 180°
Означення синуса, косинуса, тангенса, котангенса для будьякого кута від 0° до 180°
Геометрія
Декартові координати на площині
Означення синуса, косинуса, тангенса, котангенса для будьякого кута від 0° до 180°
Візьмемо коло на площині Oxy з центром у початку координат і радіусом R.
Відкладемо від додатної півосі Ox кут  у верхню півплощину (див. рисунок нижче). Точку перетину сторони кута з колом назвемо
у верхню півплощину (див. рисунок нижче). Точку перетину сторони кута з колом назвемо 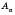 . Вона має координати
. Вона має координати 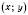 .
.
Тоді 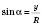 ;
; 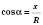 ;
; 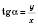 ;
; 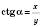 .
.
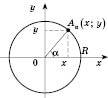
При такому означенні:
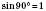 ;
; 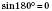 ;
;
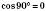 ;
; 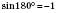 ;
;
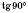 не існує;
не існує; 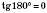 ;
;
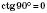 ;
; 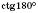 не існує.
не існує.
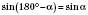 ;
;
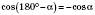 ;
;
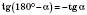
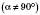 .
.
Related posts:
- Означення кута. Рiвнiсть кутiв. Бiсектриса кута. Вимiрювання та вiдкладання кутів Урок № 5 Тема. Означення кута. Рiвнiсть кутiв. Бiсектриса кута. Вимiрювання та вiдкладання кутів Мета: домогтися вiд учнiв засвоєння змiсту таких понять: “кут”, “елементи кута”, “позначення кута”, “внутрiшня область кута”, “промiнь, що дiлить даний кут на два кути”, “розгорнутий кут”, “рiвнi кути”, “бісектриса кута та аксiоми вимiрювання і вiдкладання кутiв”, “види кутiв”. Сформувати вмiння: – […]...
- Многогранники Геометрія Многогранники Двогранним кутом називається фігура, утворена двома півплощинами зі спільною прямою, що їх обмежує, – ребром двогранного кута. Півплощини називаються Гранями двогранного кута. Площина, перпендикулярна до ребра двогранного кута, перетинає його грані по двох півпрямих. Кут, утворений такими півпрямими, називається Лінійним кутом двогранного кута (див. рисунок). За міру двогранного кута приймається міра його лінійного […]...
- Кут. Вимірювання кутів. Бісектриса кута Розділ 1. Елементарні геометричні фігури та їхні властивості § 3. Кут. Вимірювання кутів. Бісектриса кута 33. 1) М – вершина кута, МА і МК – сторони кута АМК; 2) L – вершина кута, LP і LF – сторони кута PLF; 3) N – вершина кута, NB i NC – сторони кута BNC. 34. 1) O […]...
- Означення. Аксіоми Геометрія Основні властивості найпростіших геометричних фігур Означення. Аксіоми Геометрія – це наука про властивості геометричних фігур. Зверніть увагу: геометрична фігура – це не тільки трикутник, коло, піраміда тощо, а й будь-яка множина точок. Планіметрія – це розділ геометрії, у якому вивчаються фігури на площині. Точка і Пряма є основними поняттями планіметрії. Це означає, що цим […]...
- Аксіоми стереометрії Геометрія Стереометрія Аксіоми стереометрії I. Яка б не була пряма, існують точки, що належать цій прямій, і точки, що не належать їй. Через будь-які дві точки можна провести пряму, й тільки одну. II. Із трьох точок на прямій одна й тільки одна лежить між двома іншими. III. Кожний відрізок має певну довжину, більшу від нуля. […]...
- Трапеція Геометрія Чотирикутники Трапеція Трапецією називається чотирикутник, у якого тільки дві протилежні сторони паралельні. Ці сторони називаються Основами трапеції, а дві інші – Бічними сторонами. Трапеція, в якої бічні сторони рівні, називається Рівнобічною (див. рисунок нижче зліва). Якщо одна з бічних сторін трапеції перпендикулярна до основ, трапеція називається Прямокутною (рисунок нижче справа). Теорема 1. Кути трапеції, […]...
- Перпендикулярність площин Геометрія Стереометрія Перпендикулярність площин Дві площини, що перетинаються, називаються Перпендикулярними, якщо третя площина, перпендикулярна до прямої перетину цих двох площин, перетинає їх по перпендикулярних прямих (див. рисунок). Будь-яка площина, перпендикулярна до прямої перетину перпендикулярних площин, перетинає їх по перпендикулярних прямих. Ознака перпендикулярності площин Теорема 1. Якщо площина проходить через пряму, перпендикулярну до другої площини, то […]...
- Розв’язування задач геометричного змісту Урок № 126 Тема. Розв’язання задач геометричного змісту 1. На координатній прямій позначте точку D(-3) і точку С, щоб довжина CD дорівнювала 2,5 одиничних відрізки. Визначте координату точки С. Скільки розв’язків має задача? 2. Знайдіть площу і периметр чотирикутника ABCD, якщо A(-1; 2); B(3; 2); С(3; -4); D(-1; -4). 3. Знайдіть площі заштрихованих фігур, зображених […]...
- Пропорційність відрізків хорд і січних кола Геометрія Кути, пов’язані з колом Пропорційність відрізків хорд і січних кола Теорема 1. Якщо хорди AB і CD кола перетинаються в точці S, то (рисунок 1). Теорема 2. Якщо з точки P до кола проведені дві січні, що перетинають коло відповідно в точках A, B, C, D, то (рисунок 2). Тобто добуток січної, проведеної до […]...
- Коло Геометрія Основні властивості найпростіших геометричних фігур Коло Колом називається фігура, яка складається з усіх точок площини, рівновіддалених від даної точки. Ця точка називається Центром кола. Відстань від точок кола до його центра називається Радіусом кола. Радіусом також називається будь-який відрізок, що сполучає точку кола з його центром. Відрізок, що сполучає дві точки кола, називається Хордою. […]...
- Ознака паралельності площин Геометрія Стереометрія Ознака паралельності площин Теорема 1. Якщо дві прямі однієї площини, які перетинаються й відповідно паралельні двом прямим другої площини (див. рисунок), то ці площини паралельні. Теорема 2 (обернена). Якщо в одній площині є дві прямі, які перетинаються, і ці прямі паралельні другій площині, то такі площини паралельні. Зверніть увагу: прямі мають обов’язково перетинатися. […]...
- Кут між площинами Геометрія Стереометрія Кут між площинами Кут між паралельними площинами вважається таким, що дорівнює . Нехай дані площини перетинаються (див. рисунок). Проведемо площину, перпендикулярну до прямої їх перетину. Ця площина перетинає дані площини по двох прямих. Кут між цими прямими називається Кутом між даними площинами. Означений таким чином кут між площинами не залежить від вибору січної […]...
- Тригонометричні функції кута УРОК 5 Тема. Тригонометричні функції кута Мета уроку: повторити означення тригонометричних функцій гострого кута прямокутного трикутника і ввести означення тригонометричної функції довільного кута. І. Аналіз помилок, допущених у математичному диктанті та самостійній роботі. 1. Побудуйте графіки функцій (індивідуальні картки): А) ; б) ; в) ; г) . Відповідь: а) рис. 25; б) рис. 26; в) […]...
- Кути, вписані в коло Геометрія Кути, пов’язані з колом Кути, вписані в коло Кут розбиває площину на дві частини. Кожна із цих частин називається Плоским кутом. Плоскі кути із спільними сторонами називаються Доповняльними. Якщо плоский кут є частиною півплощини, то його градусною мірою називається градусна міра звичайного кута з тими самими сторонами. Центральним кутом у колі називається плоский кут […]...
- Величина кута. Вимірювання і побудова кутів Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 20.Величина кута. Вимірювання і побудова кутів Кути, як і відрізки, можна вимірювати. Поділимо прямий кут на 90 рівних частин (рис. 100). Міру однієї такої частини беруть за одиницю вимірювання кутів і називають градусом1. Позначають так: 1°. Градусна міра прямого кута дорівнює 90°, […]...
- Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Візьмемо три взаємно перпендикулярні прямі Oх, Oy, Oz, які перетинаються в одній точці О (див. рисунок). Проведемо через кожну пару цих прямих площину. Площина, яка проходить через прямі Oх і Oу, називається площиною Oxy. Дві інші площини називаються відповідно Oxz і Oyz. Прямі Ox, Oy, Oz називаються Координатними […]...
- ЯК ЗАЛЕЖИТЬ ОСВІТЛЕНІСТЬ ВІД КУТА ПАДІННЯ СВІТЛА? РОЗДІЛ 3. СВІТЛОВІ ЯВИЩА §24 . СИЛА СВІТЛА Й ОСВІТЛЕНІСТЬ 3. ЯК ЗАЛЕЖИТЬ ОСВІТЛЕНІСТЬ ВІД КУТА ПАДІННЯ СВІТЛА? Освітленість поверхні залежить не тільки від сили світла джерела та відстані до нього: вона ще залежить від кута падіння світла. І дуже істотно: саме цим, як ми зараз побачимо, зумовлено, наприклад, зміну пори року! У разі збільшення […]...
- Координатна площина Урок № 113 Тема. Координатна площина Мета: відпрацювати навички “читати” готові рисунки з точкам на координатній площині та будувати точки із заданими координатами; здійснити діагностику знань і вмінь з теми. Тип уроку: застосування знань, умінь, навичок. Хід уроку I. Організаційний момент II. Перевірка домашнього завдання @ Бажано звернути увагу на задачу 4 – повторити спосіб […]...
- Тригранний і многогранний кути Геометрія Многогранники Тригранний і многогранний кути Нехай промені a, b, c виходять з однієї точки й не лежать в одній площині. Тригранним кутом називається фігура, яка складається з трьох плоских кутів , , (див. рисунок). Ці кути називаються Гранями тригранного кута, а їх сторони – Ребрами. Спільна вершина плоских кутів називається Вершиною тригранного кута. Двогранні […]...
- Перпендикулярність прямих і площин Геометрія Стереометрія Перпендикулярність прямих і площин Дві прямі називаються Перпендикулярними, якщо вони перетинаються під прямим кутом. Теорема 1. Якщо дві прямі, які перетинаються, паралельні відповідно двом іншим перпендикулярним прямим, то інші прямі теж перпендикулярні. Теорема 2. Через будь-яку точку прямої у просторі можна провести безліч перпендикулярних до неї прямих (див. рисунок). (Усі прямі лежать у […]...
- Означення трапеції. Окремі види трапецій Урок № 13 Тема. Означення трапеції. Окремі види трапецій Мета: сформувати в учнів поняття трапеції, її елементів; розглянути означення рівнобічної та прямокутної трапецій, зміст властивостей кутів трапеції, прилеглих до бічної сторони, та кутів рівнобічної трапеції. Формувати вміння: – відтворювати вивчені твердження; – виконувати рисунок за описом; – за готовим рисунком знаходити елементи трапеції; – розв’язувати […]...
- Властивості паралельних площин Геометрія Стереометрія Властивості паралельних площин Теорема 1. Якщо дві паралельні площини перетинаються третьою площиною (див. рисунок), то прямі перетину паралельні. На рисунку: ; . Теорема 2. Відрізки паралельних прямих, які містяться між двома паралельними площинами (див. рисунок), рівні. На рисунку: ; ; . Теорема 3. Нехай площини і паралельні (див. рисунок нижче) і є точка […]...
- Синус, косинус і тангенс гострого кута прямокутного трикутника Урок № 54 Тема. Синус, косинус і тангенс гострого кута прямокутного трикутника Мета: домогтися засвоєння учнями змісту означень синуса, косинуса, тангенса і котангенса гострого кута прямокутного трикутника та їх властивостей, що випливають із теореми Піфагора, подібності прямокутних трикутників та властивостей сторін прямокутного трикутника (проти більшої сторони лежить більший кут, і навпаки). Сформувати вміння відтворювати зміст […]...
- Паралельність прямих і площини Геометрія Стереометрія Паралельність прямих і площини Дві прямі в просторі називаються Паралельними, якщо вони лежать в одній площині й не перетинаються. Прямі, які не лежать в одній площині, називаються Мимобіжними. Зверніть увагу: “не лежать в одній площині” і “лежать у різних площинах” – це різні твердження. Наприклад, паралельні прямі a і b лежать у різних […]...
- Основні співвідношення між тригонометричними функціями одного й того самого кута 10. Додатки 34. Основні співвідношення між тригонометричними функціями одного й того самого кута...
- Найпростіші задачі па побудову Розділ 1. Найпростіші геометричні фігури та їх властивості § 18. Найпростіші задачі па побудову 708. Щоб побудувати трикутник, що дорівнює трикутнику ABC, треба провести три кола радіусами 5 см, 6 см і 9 см. 709. 710. 1) AС = 5 см; 2) AС = 0,35 дм; 3) AС = 43 мм. 711. 1) Будуємо відрізок […]...
- Симетрія відносно точки Геометрія Рух Симетрія відносно точки Нехай O – фіксована точка, X – довільна точка площини. Відкладемо на продовженні відрізка OX за точку O відрізок , що дорівнює OX. Точка називається Симетричною точці X відносно точки O (див. рисунок). Очевидно, що точка, симетрична , є точка X. Перетворення фігури F у фігуру , при якому кожна […]...
- Рівняння сфери, площини і прямої 79. (x – 1)2 + у2 + (2 – 4)2 = 25. 80. A(10; 0; 0), В(0; 10; 0), С(0; 0; 10). 81. M(3; 2; -1) не належить сфері. X2+ у2 + z2 – 2х + 4у – 6z – 2 = 0, бо 32 + 22 + (-1)2 – 2 × 3 + 4 […]...
- Перпендикулярні та паралельні прямі. Координатна площина Урок № 119 Тема. Перпендикулярні та паралельні прямі. Координатна площина Мета: перевірити й оцінити рівень знань та вироблених умінь і навичок, які є обов’язковими для опанування теми. Тип уроку: контроль і корекція знань, умінь та навичок. Хід уроку I. Організаційний момент II. Перевірка домашнього завдання Збираємо зошити з домашньою контрольною роботою для перевірки. III. Умова […]...
- Метод координат. Рівняння сфери, площини, прямої Завдання 2 1. 1) Рівняння сфери, усі точки якої рівновіддалені від початку координат на 1 од. має вигляд х2 + у2 + z2= 1. 2) Оскільки центр сфери – початок координат і вона перетинає ось Оz у точці (0; 0; 1), то вона має радіус 1, а значить, її рівняння; х2 + у2 + z2 […]...