Головна ⇒ 📌Математика ⇒ ОЗНАКИ ПАРАЛЕЛЬНОСТІ ПРЯМИХ

ОЗНАКИ ПАРАЛЕЛЬНОСТІ ПРЯМИХ

РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ

& 6. ОЗНАКИ ПАРАЛЕЛЬНОСТІ ПРЯМИХ

Важливу роль у дослідженні паралельності прямих відіграють поняття січної та деяких пар кутів.

Нехай а і b – дві довільні прямі площини. Пряму с, що їх перетинає, називають січною прямих а і b (мал. 73).

Прямі а і b з їх січною с утворюють 8 кутів. На малюнку 73 їх пронумеровано.

Деякі пари цих кутів мають спеціальні назви: внутрішні різносторонні кути: 1 і 3, 2 і 4; внутрішні односторонні кути: 1 і 4, 2 і 3; відповідні кути: 1 і 8, 2 і 7, 3 і 6, 4 і 5. Зверніть увагу!

Якщо два які-небудь внутрішні різносторонні кути рівні, то рівні також внутрішні різносторонні кути іншої пари (мал. 74). Якщо, наприклад, ∠1 = ∠3, ТО ∠2 = ∠4, бо кути, суміжні з рівними, – рівні.

Випадок, коли внутрішні різносторонні кути рівні, заслуговує на особливу увагу, тому що саме за цієї умови прямі а і b паралельні.

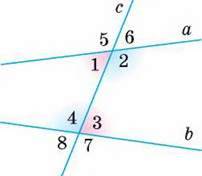
Мал. 73

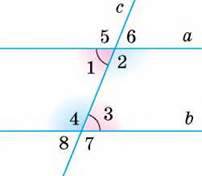
Мал. 74

Теорема 3 (ознака паралельності прямих)

Дві прямі паралельні, якщо із січною вони утворюють рівні внутрішні різносторонні кути.

Доведення. Нехай січна АВ перетинає прямі a i b так, що утворені при цьому

внутрішні різносторонні кути 1 і 3 дорівнюють один одному. Тоді, як показано ви ще, кути 2 і 4 також рівні. Припустимо, що за такої умови прямі а і b перетинаються в якійсь віддаленій точці С. У результаті утвориться трикутник ABC (на малюнку 75 схематично його зображено у вигляді п’ятикутника). Уявимо, що цей трикутник повернуто навколо точки О – середини відрізка АВ – так, щоб відрізок ОА зайняв положення ОВ. Тоді, оскільки ∠1 = ∠3 і ∠2 = ∠4, промінь АС суміститься з променем ВК, а промінь ВС – з променем АР. Оскільки промені АС і ВС (за припущенням) мають спільну точку С, то промені ВК і АР також мають якусь спільну точку С1 А це означає, що через дві точки С і С1, проведено дві різні прямі. Такого не може бути.

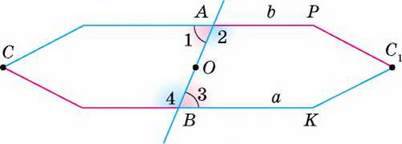
Мал. 75

Отже, якщо ∠1 = ∠3, то прямі а і b не можуть перетинатися. А оскільки вони лежать в одній площині і не перетинаються, то вони паралельні: а ‖ b. Це й треба було довести.

Зверніть увагу на спосіб доведення теореми 3. Щоб довести, що прямі а і b паралельні, ми показували, що вони не можуть перетинатися. Тобто припускали супротивне тому, що треба було довести. Такий спосіб міркувань називають методом доведення від супротивного.

На основі доведеної теореми 3 неважко довести й інші ознаки паралельності прямих.

Теорема 4 Дві прямі паралельні, якщо при перетині з січною вони утворюють внутрішні односторонні кути, сума яких дорівнює 180°.

Доведення. Нехай, наприклад, на малюнку 76 сума внутрішніх односторонніх кутів 1 і 4 дорівнює 180°. Сума суміжних кутів 3 і 4 також дорівнює 180°. Тому ∠1 = ∠3. Це – внутрішні різносторонні кути. Якщо вони рівні, то прямі a i b паралельні.

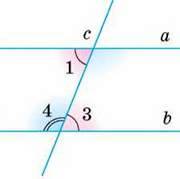
Мал. 76

Теорема 5 Дві прямі паралельні, якщо, перетинаючись із січною, вони утворюють рівні відповідні кути.

Доведення. Нехай січна с перетинає прямі а і b так, що утворені при цьому відповідні кути 1 і 8 рівні (мал. 77). Кути 8 і 3 рівні, бо вертикальні. Тому якщо ∠1 = ∠8, ∠8 = ∠3, то і ∠1 = ∠3, звідси випливає, що а ‖ b.

Заслуговує на увагу такий наслідок із теореми 3.

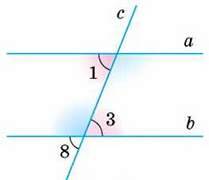
Мал. 77

Наслідок Дві прямі, перпендикулярні до третьої прямої, паралельні.

Адже якщо кожна з прямих а і b перпендикулярна до с, то утворені при цьому внутрішні різносторонні кути рівні, бо вони дорівнюють по 90° (мал. 78). Отже, прямі а і b – паралельні.

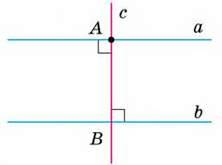
Мал. 78

Для допитливих

1. Кути 5 і 7( а також 6 і 8) називають зовнішніми різносторонніми, а 5 і 8 (а також 6 і 7) – зовнішніми односторонніми кутами (мал. 79). Використовуючи ці поняття, спробуйте сформулювати і довести ще дві ознаки паралельності прямих.

2. Корисно краще зрозуміти сутність методу доведення від супротивного.

Якщо твердження А заперечує твердження В, то такі два твердження називають суперечливими або супротивними одне одному. Із двох взаємно суперечливих тверджень завади одне правильне, а інше – хибне. Тому якщо переконаємося, що твердження А і В суперечливі одне одному і, наприклад, що В неправильне, то можемо бути певні, що твердження А – правильне.

Не слід плутати твердження супротивні з протилежними. Наприклад, якщо йдеться про числові

Вирази і натуральні числа, то твердження: “вираз А – додатний” і “вираз А – від’ємний” або “число n – просте” і “число n – складене” – протилежні, але не супротивні, адже кожне з них може бути неправильним. А от твердження “вираз А – додатний” і “вираз А – недодатний” або “число n – просте” і “число n – непросте” – взаємно суперечливі. Непросте – означає складене або дорівнює 1; недодатне – від’ємне або дорівнює нулю.

Доводячи методом від супротивного, спростовувати треба не протилежне твердження, а супротивне даному.

Спростувати що-небудь – означає показати, що воно неправильне.

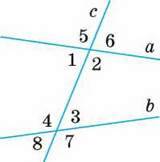
Мал. 79

Запитання і завдання для самоконтролю

1. Сформулюйте означення паралельних прямих.

2. Що таке січна двох прямих?

3. Які кути називають внутрішніми різносторонніми? А внутрішніми односторонніми? Покажіть на малюнку.

4. Які кути називають відповідними? Покажіть на малюнку.

5. Сформулюйте і доведіть ознаки паралельності прямих.

Виконаємо разом

1. Як побудувати паралельні прямі, користуючись лише лінійкою і транспортиром?

Накреслимо довільний промінь АВ і відкладемо рівні кути ВАС і АСР, як показано на малюнку 80. Прямі АВ і СР – паралельні, адже кути ВАС і АСР – внутрішні різносторонні, а за побудовою вони рівні.

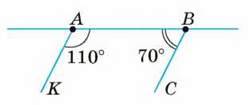
2. Через кінці відрізка АВ з одного боку від прямої АВ проведено промені АK і ВС так, що ∠КАВ = 110°, а ∠АВС = 70°. Чи паралельні ці промені?

– Пряму АВ можна вважати січною прямих АК i ВС (мал. 81).

Кути КАВ і ABC – внутрішні односторонні. Оскільки їх сума 110° + 70° дорівнює 180°, то прямі АК і ВС – паралельні (теорема 4).

Тому і промені АК і ВС – паралельні.

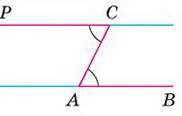
Мал. 80

Мал. 81

ЗАДАЧІ І ВПРАВИ

Виконайте усно

164. Скільки кутів утворюється при перетині двох прямих третьою?

165. Розгляньте малюнок 82 і назвіть пари кутів:

А) внутрішніх різносторонніх;

Б) внутрішніх односторонніх;

В) зовнішніх різносторонніх;

Г) зовнішніх односторонніх; г) відповідних;

Д) суміжних;

Е) вертикальних.

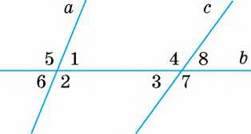
Мал. 82

166. Використовуючи малюнок 82, знайдіть суми мір кутів:

А) 1, 2, 3 і 4; 6)1,3, 5 і 7; в) 1,4, 5 і 8; г) 5, 6, 7 і 8.

167. Чи паралельні прямі а і с на малюнку 82, якщо:

A) ∠6 = ∠8; б) ∠7 = 101° і ∠5 = 101°;

В) ∠5 + ∠8 = 180°; г) ∠1 + ∠7 = 180°?

168. Як розташовані прямі а і b, якщо а ⏊ с, b ⏊ с і всі вони лежать в одній площині?

169. Як можуть бути розміщені в просторі прямі а і b, якщо а ⏊ с і b А⏊ с?

170. Запишіть назви пар кутів, зображених на малюнку 82:

А) ∠1 і ∠5; в) ∠7 і ∠2; г) ∠2 і ∠3;

Б) ∠6 і ∠3; г) ∠3 і ∠1; д) ∠8 і ∠5.

171. Відомо, що ∠1 = 87°, ∠ 78° (див. мал. 82). Обчисліть міри кутів 2, 4, 5, 6, 7, 8.

172. Скориставшись малюнком 82, обчисліть:

А) міри кутів 1, 2, 3, 4, 5, 8, якщо ∠7 = 100°, ∠6 = 90°;

Б) ∠1 + ∠4 і ∠2 + ∠3, якщо ∠5 + ∠8 = 170°;

В) ∠4 – ∠5, якщо ∠4 – ∠2 = 10°.

173. Чи паралельні прямі а і с (див. мал. 82), якщо:

А) ∠1 = 50°, ∠7 = 130°;

Б) ∠6 = 65°; ∠8 = 65°;

В) ∠1 + ∠7 = 180°;

Г) ∠2 = 140°, ∠3 на 80° менший від ∠2?

174. ВМ – бісектриса кута КВС (мал. 83). Чи паралельні прямі АС і ВМ, якщо ∠A = 50° і:

А) ∠СВМ = 50°;

Б) ∠АВМ = 130°;

В) ∠BCA = ∠КВМ;

Г) ∠ABM на 50° більший за ∠CAB?

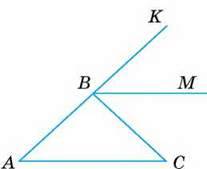
Мал. 83

175. Пряма КР перетинає пряму АВ в точці К, а пряму CD – у точці Р. Чи паралельні прямі АВ і CD, якщо ∠АКР = 90° і ∠КРС = 90°?

176. Пряма КР перетинає пряму АВ в точці К, а пряму CD – у точці Р так, що точки В i D лежать по один бік від прямої КР. Чи паралельні прямі АВ і CD, якщо ∠BKP = 89°39′ і ∠KPD = 90°21′?

177. Через кінці відрізка АВ з одного боку від нього проведено промені АР і ВС. Чи паралельні ці промені, якщо:

А) ∠РАB = 105°, a ∠ABC = 75°;

Б) ∠РАB = 93°, а ∠АВС = 87°?

178. Доведіть, що протилежні сторони прямокутника лежать на паралельних прямих.

179. Прямі а і b з січною с утворюють рівні гострі кути. Чи випливає з цього, що а ‖ b?

180. Знайдіть міри кутів 1 і 2, зображених на малюнку 84, якщо ∠1 + ∠4 = 160° і:

А) ∠4 на 20° менший від ∠1;

Б) ∠2 у 2 рази більший за ∠1;

В) ∠4 : ∠2 = 2 : 3;

Г) ∠4 становить 60 % кута 2.

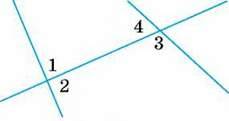
Мал. 84

181. Чи паралельні прямі а і b, зображені на малюнку 85, якщо:

А) ∠4 – ∠1 = 30° і ∠3 = 75°;

Б) ∠1 = 60° і ∠2 : ∠3 = 2 : 1?

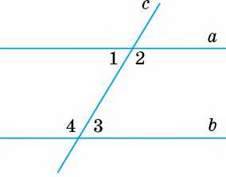
Мал. 85

182. Установіть взаємне розташування прямих а, b, с, зображених на малюнку 86, якщо:

А) ∠3 = ∠5 = ∠9;

Б) ∠2 = ∠8 i ∠7 = ∠9;

В) ∠12 = ∠8 і ∠6 + ∠3 = 180°.

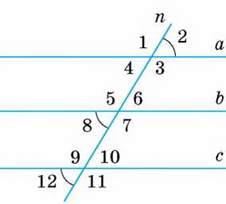
Мал. 86

183. Січна n перетинає прямі а, b і с так, що кути позначені на малюнку 86 числами 2, 8 і 12, дорівнюють один одному. Доведіть, що прямі а, b і с попарно паралельні.

184. У зображеному на малюнку 87 шестикутнику∠1 = ∠4, ∠2 = ∠5 і ∠3 = ∠6. Доведіть, що кожна сторона даного шестикутника паралельна протилежній стороні.

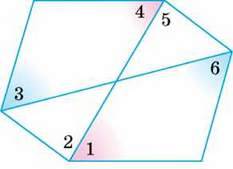
Мал. 87

185. Чи паралельні прямі а і b, с і d, якщо: ∠1 = 60°, ∠2 – удвічі більший, a ∠2 – ∠3 = 60° (мал. 88)?

186. Як можна побудувати паралельні прямі, користуючись косинцем?

187. Користуючись двома однаковими косинцями, паралельні прямі можна проводити, як показано на малюнку 89. Обгрунтуйте таку побудову.

188. Закінчіть речення: “Щоб дізнатися, чи паралельні дані прямі, треба провести їх січну і виміряти відповідні кути. Якщо…”

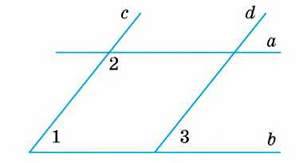
Мал. 88

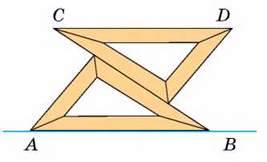
Мал. 89

Практичне завдання

189. Зробіть модель для ілюстрації доведення теореми 3.

ВПРАВИ ДЛЯ ПОВТОРЕННЯ

190. Сторони трикутника дорівнюють 12 см, 15 см і 18 см. У скільки разів зменшиться периметр трикутника, якщо кожну його сторону зменшити на 5 см?

191. Точки К, L і М лежать на одній прямій. KL = 7 см, LM = 3 см. Знайдіть КМ. Розгляньте всі можливі випадки.

192. Прямі АВ і CD перетинаються в точці О, ОМ – бісектриса кута AОС. Знайдіть міри кутів МОВ і MOD, якщо ∠COB = 70°.

193. Один із двох кутів, утворених при перетині двох прямих, на 90° більший за інший. У скільки разів він більший за інший кут?

(1 votes, average: 5.00 out of 5)

Ви зараз читаєте: ОЗНАКИ ПАРАЛЕЛЬНОСТІ ПРЯМИХ

« Творення й відмінювання активних і пасивних дієприкметників теперішнього й минулого часу

МАТКОВА СІМ’Я »

РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ

& 6. ОЗНАКИ ПАРАЛЕЛЬНОСТІ ПРЯМИХ

Related posts: