Перетворення виразів (повторення та систематизація матеріалу, вивченого в 5 та 6 класах)
Урок № 2
Тема. Перетворення виразів (повторення та систематизація матеріалу, вивченого в 5 та 6 класах)
Мета: повторити та систематизувати відомості про види перетворень виразів та способи дій, передбачених ними, що були отримані учнями в 5-6 класах в обсязі, необхідному для сприйняття теми “Рівняння”.
Тип уроку: повторення, систематизація знань, умінь, навичок.
Хід уроку
I. Організаційний момент
II. Перевірка домашнього завдання
@ Оскільки вправи, аналогічні до № 1 і 2 домашнього завдання, досить ретельно опрацьовані
III. Робота з випереджальним домашнім завданням (Повторення та систематизація знань)
Варіант
1. Заповніть пропуски в реченнях, щоб твердження були правильними. |
А) Щоб…, перед якими стоїть знак”+”, треба опустити дужки і знак “+”, що стоїть перед ними, і записати всі доданки зі… знаками. |
Б) Щоб…, перед якими стоїть знак “-“, треба опустити дужки і знак “-“, що стоїть перед ними, і записати всі доданки з… знаками. |
В) Щоб… доданки, треба додати їх коефіцієнти і результат помножити на спільну буквену частину. |
Г) Заміна виразу ас + bс на… називається… множника за дужки. |
Д) Заміна виразу а(b + с) на… називається розкриттям… |
Є) Для будь-яких раціональних чисел а, b і с справджується рівність ab = … та (ab)c = … |
2. Із запропонованих виразів виберіть приклади до кожного з наведених вище алгоритмів і перетворіть ці вирази, використовуючи відповідний алгоритм: |
А) -2а(+2с – 3m); б) -9х + 7х – 5x + 2х; в) 54 – 4 – 14 – 54; |
Г) a + b – (b – c) + d; д) а – b + (b – с) + 1,8; е) -7,2 – х – 10 |
По закінченні перевіряємо й корегуємо виконані завдання.
Варіант 2. Робота в групах. За основу беремо ті ж самі 5 алгоритмів (див. 1-й варіант), але кожна група отримує один з алгоритмів, наприклад, у вигляді набору карток, на яких записані окремі частини алгоритмів. Завдання кожної групи полягає в тому, щоб:
1) з окремих слів скласти речення, що виражало б певний алгоритм;
2) підібрати приклад, що ілюструє застосування алгоритму;
3) підготувати й здійснити презентацію своєї роботи.
У будь-якому разі мета цієї частини уроку: повторити алгоритми основних видів перетворень виразів, що були вивчені учнями в 5-6 класах, та найголовніше – відтворити способи дій, що передбачаються в цих алгоритмах.
IV. Узагальнення та систематизація вмінь і навичок
Виконання усних вправ
1. Чи правильно розкрито дужки?
1) 3 + (-5 – 2) = 3 – 5 – 2;
2) 3 – (5 – 2) = 3 – 5 – 2;
3) 3 – (5 + 2) = 3 + 5 – 2;
4) 3 – (5 + 2) = 3 – 5 + 2?
2. Назвіть коефіцієнти виразів: 3ху; – у; -1,2а; –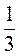 B; т.
B; т.
3. Назвіть подібні доданки у виразах: х – 2у +3х – у; 7b – a – 2ab + b + 3ab.
4. Розкрийте дужки:(х – у) – 5; (a + b – c) – 4; – a(b + c).
Виконання письмових вправ
1. Спростіть вирази:
1) -1,2 – 3а;
2) -5b – 2,4с;
3) –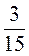 Х –
Х – 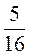 – (-у).
– (-у).
2. Розкрийте дужки у виразах:
1) 2(x – 7y + 3z); 2) (c – 8d + 6k) – (-1,2); 3) – b(-x + 2y – 4,6).
3. Зведіть подібні доданки:
1) 8a + 19a – 28a + 3a;
2) 1,4a – a + b – 2,6b;
3) 1,6m – 1,3 – 3,1m + 0,8;
4) –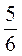 A +
A + 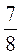 B +
B + 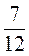 A –
A – 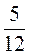 B.
B.
4. Розкрийте дужки і зведіть подібні доданки:
1) 7(4а + 6) – 12а;
2) 8х – 4(16 – 2х);
3) 1,7(a – 4) + 0,6(6 – 2а);
4) -(4,3х – 2,4) – (5,8 – 2,6х);
5) 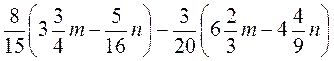
5*. Спростіть вирази:
1) х – (2x – (4x + 3));
2) 8m – (4n – 6m + (3n + 5m)).
6*. Доведіть, що значення виразу не залежить від значення змінної:
1) 3(x – 2) – 5(4 + x) + 2(x + 13);
2) 2a – (a – (1 + 4a)) + 4 – a – (4a – 7).
7*. Відшукайте пропущений запис:
Опадання листя восени | Листопад |
(2a + 3b) – (3a + 2b) | ? |
V. Рефлексія
Цей етап уроку можна провести у вигляді гри “Кошик знань”. Кожний з учнів самостійно оцінює свої здобутки і кладе в “Кошик знань” відповідного кольору або форми предмет (наприклад, якщо учень вважає, що матеріал уроку засвоєно ним повністю, то він кладе зелений кружечок; якщо вважає, що більшість матеріалу засвоєна, але залишились деякі незрозумілі моменти, то кладе жовтий кружечок; якщо ж вважає, що майже все на уроці було незрозумілим – кладе червоний кружечок).
Після цього вчитель разом з учнями аналізує ситуацію, що склалася, дає вербальну оцінку результатів, з’ясовує, які питання були найскладнішими і над чим треба більш ретельно попрацювати вдома.
VI. Домашнє завдання
№ 1. Спростіть вирази. Пронумеруйте, які саме перетворення виразів були використані в кожному окремому випадку.
1) -0,8х – (-0,7);
2) 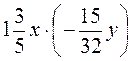 ;
;
3) -7 – (5 – а – 4b);
4) -0,6х(-5 + 3m – 1,4n);
5) -4х + 11x + 35x – 38x;
6) 1,1p + 0,9d – 1,2 – 1,3p – 3,8d;
7) 14,5(8х – 6y) – (5y – 3х) – 2,4;
8) 0,6(4х – 12) – 0,4(5х – 7).
№ 2. Випереджальне домашнє завдання.
Серед математичних записів один зайвий. Поясніть, який та чому?
1) 3х + 2 = 5;
2) 3 + 2 = 5х;
3) 3 + 2 = 5;
4) 3х + 2х = 5.
До кожної з рівностей, що ви залишили, придумайте задачу. (Під час виконання цієї роботи можна використовувати п. 1 підручника.)