Побудова правильних многокутників
УРОК № 19
Тема. Побудова правильних многокутників
Мета уроку: ознайомлення учнів з правилами побудови правильних многокутників (зокрема трикутників, чотирикутників і шестикутників).
Тип уроку: комбінований.
Вимоги до рівня підготовки учнів: будують правильний трикутник, чотирикутник і шестикутник.
Хід уроку
І. Перевірка домашнього завдання
Двоє учнів відтворюють за відкидними дошками розв’язування домашніх задач 1 і 2, а в цей же час клас пише математичний диктант.
Задача 1. Розв’язання
Нехай сторона
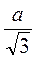і R = 
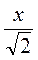.Звідси = ;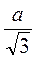 
.
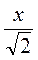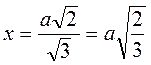Відповідь.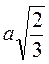 
.
Задача 2. Розв’язання
Якщо радіус кола дорівнює 4 см, то сторона вписаного трикутника дорівнює 4
см. Ураховуючи, що сторона квадрата дорівнює 4 см, радіус кола, описаного навколо квадрата, дорівнює 
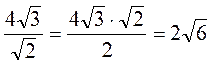(см).
Відповідь. 2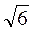
см.
Математичний диктант.
Дано
Варіант 1 – 6 см; варіант 2 – 8 см.
Знайдіть:
А) сторону правильного трикутника, вписаного в це коло;
Б) сторону правильного трикутника, описаного навколо цього кола;
В) сторону правильного чотирикутника, описаного навколо даного кола;
Г) сторону правильного чотирикутника, вписаного в дане коло;
Д) сторону правильного шестикутника, вписаного в дане коло;
Є) периметр правильного шестикутника, описаного навколо цього кола.
Відповіді
Варіант 1. а) 6 см; б) 12 см; в) 12 см; г) 6
см; д) 6 см; є) 24 см.
Варіант 2. а) 8 см; б) 16 см; в) 16 см; г) 8 см; д) 8 см; є) 32 см.
ІІ. Розв’язування задач
Колективне розв’язування задач
1) Кінець гвинта газової засувки має правильну тригранну форму. Який найбільший розмір може мати кожна грань, якщо діаметр циліндричної частини гвинта дорівнює 2 см?
Розв’язання
Кожна грань може мати найбільший розмір, якщо кінець гвинта газової засувки, який має форму правильного трикутника, буде вписаний в коло діаметром 2 см. Отже, сторона трикутника дорівнює: R= 
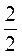• = (см).
Відповідь. см.
2) Доведіть, що сторона правильного 12-кутника обчислюється за формулою а12 =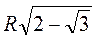 
, де R – радіус описаного кола.
Доведення
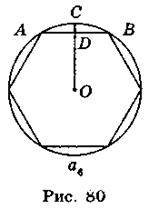
Нехай АВ – сторона вписаного правильного шестикутника (рис. 80). АС – сторона вписаного правильного 12-кутника. Із прямокутного трикутника ACD маємо:
АС =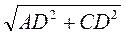 
, де AD = 
= 
,
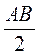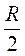CD = OC – OD = R –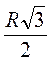 
Тоді АС =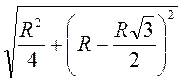 
= 
= 
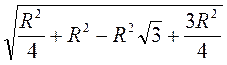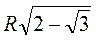що і треба було довести.
III. Самостійна робота
Самостійна робота навчального характеру запропонована у двох варіантах. Двоє учнів виконують роботу за відкидними дошками, а решта – у зошитах. Після закінчення виконати перевірку за записами, зробленими на відкидних дошках.
Варіант 1
1. Сторона правильного многокутника дорівнює а, а радіус описаного навколо нього кола R. Знайдіть радіус вписаного кола. 2. Виразіть сторону b правильного описаного навколо кола многокутника через радіус R кола і сторону а правильного вписаного многокутника з тією самою кількістю сторін.
Варіант 2
1. Сторона правильного многокутника а, а радіус вписаного в нього кола r. Знайдіть радіус описаного кола. 2. Виразіть сторону а правильного вписаного в коло многокутника через радіус R кола і сторону b правильного описаного многокутника з тією самою кількістю сторін.
Розв’язання завдань самостійної роботи
Варіант 1
1. Нехай АВ = ВС = а, OB = R (рис. 81), OD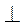
AB, тоді BD = = 
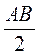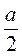. Із трикутника ODB маємо:
OD =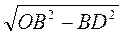
= 
.
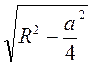Відповідь. .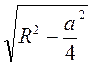
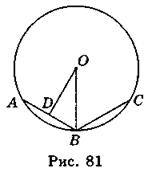
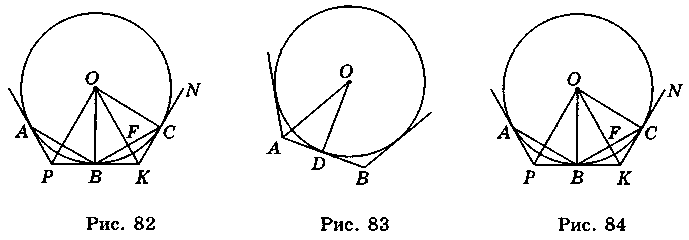
2. Нехай ABC… – правильний вписаний многокутник, a PKN… – правильний описаний многокутник (рис. 82). Трикутники ОВС і ОРК подібні, оскільки вони мають рівні кути. Із подібності трикутників маємо: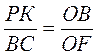 
. Звідси РК = 
= 
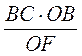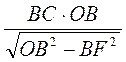. Ураховуючи, що ВС = а, OB = R, маємо:
.
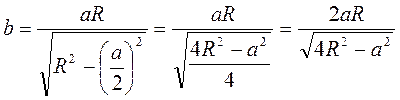Відповідь.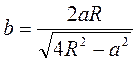 
.
Варіант 2
1. Нехай АВ = а, DO = r (рис. 83). OD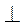AB, тоді AD = 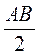= 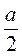. Із трикутника ADO маємо: АО = 
= 
.
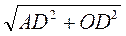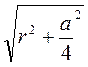Відповідь. .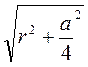
2. Нехай ABC… – правильний вписаний многокутник, a PKN… – правильний описаний многокутник (рис. 84). ?ОВС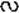 
?ОРК, тобто 
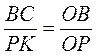. Звідси ВС = 
= 
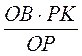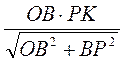. Ураховуючи, що PK = b, OB = R, маємо:
.
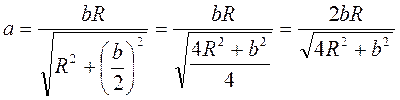Відповідь.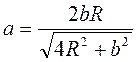 
.
IV. Сприймання й усвідомлення нового матеріалу
Фронтальна бесіда
1) Як можна побудувати правильний шестикутник? 2) Побудовано правильний шестикутник. Як на цьому рисунку побудувати правильний трикутник? 3) Як можна побудувати правильний чотирикутник? 4) Як можна побудувати правильний восьмикутник?
Виконання вправ
1) Впишіть у дане коло квадрат. 2) Впишіть у дане коло правильний шестикутник. 3) Впишіть у дане коло правильний трикутник. 4) Опишіть навколо кола правильний восьмикутник.
Розв’язання
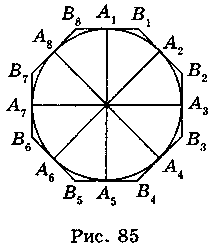
Ділимо коло на вісім рівних частин. (Для цього проводимо два взаємно перпендикулярні діаметри А1А5 і А3А7; чотири утворені дуги ділимо навпіл (рис. 85).)
Через точки А1, А2, А3, А4, А5, A6, А7, A8 поділу кола на вісім частин проводимо дотичні до кола. Утворений многокутник – описаний правильний восьмикутник.
V. Домашнє завдання
Розв’язати задачі.
1. Кінець валика діаметром 4 см обпилено у вигляді квадрата. Визначте, який найбільший розмір може мати сторона квадрата. 2. Доведіть, що сторона правильного шестикутника обчислюється за формулою а8 = R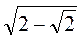
, де R – радіус описаного кола.
VI. Підбиття підсумків уроку
Запитання до класу
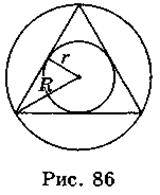
1. Як можна описати навколо кола правильний трикутник? 2. Як можна описати навколо кола квадрат? 3. Як можна побудувати правильний дванадцятикутник? 4. Навколо правильного трикутника описане коло, і в цей самий трикутник вписане коло (рис. 86). Радіус вписаного кола r, а радіус описаного кола – R. Визначте, які із наведених тверджень є правильними, а які – неправильними.
А) R = 2r.
Б) Центр описаного кола збігається з точкою перетину медіан трикутника.
В) Сторона трикутника дорівнює R.
Г) Сторона трикутника дорівнює r.
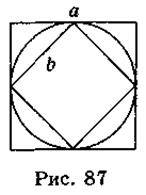
5. У коло вписано квадрат, і навколо цього самого кола описано квадрат (рис. 87). Сторона описаного квадрата дорівнює а, а сторона вписаного квадрата – b. Визначте, які з наведених тверджень є правильними, а які – неправильними.
А) a = b.
Б) Центр кола збігається з точкою перетину діагоналей вписаного квадрата.
В) Радіус кола дорівнює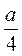 
.
Г) Радіус кола дорівнює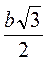 
.
(1 votes, average: 5.00 out of 5)
Loading...