Поняття об’єму
1121.
Цеглина має форму прямокутного паралелепіпеда.
Об’єм паралелепіпеда дорівнює: V = 250 × 120 × 65 = 1 950 000 мм3 = 1,95 дм3.
1122.
Для того, щоб знайти скільки кубометрів грунту перевернули, треба знайти об’єм прямокутного паралелепіпеда з площею основи 5 га і висотою 35 см.
V = 50 000 м2 × 0,35 м = 17 500 м3.
1123.
Нехай а – сторона куба.
А) Площа грані куба S = а2, а2 = Q, 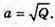
Об’єм куба 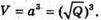
Б) Нехай ABCDA1B1C1D1 – куб, а – сторона куба.
З ΔABD: 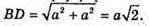
З ΔB1BD:
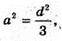
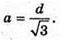
Об’єм куба 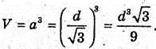
Відповідь: а) 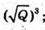 б)
б) 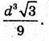
1124.
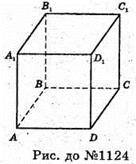
Нехай сторона основи правильної чотирикутної призми дорівнює а, тобто
AB = BC = CD = AD = а. Площа основи S = а2, 49 = а2, а = 7 (см).
Площа бічної грані S1 = а × CC1, 56 = 7CC1, CC1= 8 (см).
Vпризми = Soсн. × H = 49 × 8 = 392 (см3).
Відповідь: 392 см2.
1125.
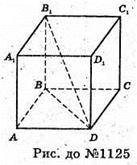
Нехай ABCDA1В1C1D1 – куб. V – об’єм куба.
Нехай а – сторона куба. V = а3, 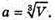
3 ΔABD: 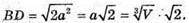
З
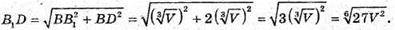
Відповідь: 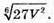
1126.
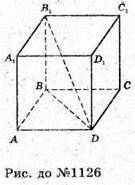
Нехай ABCDA1B1C1D1- правильна чотирикутна призма,
B1D – діагональ, B1D = d, ∠B1DB = α, а – сторона основи.
V призми = S oсн. × BB1.
З ΔBB1D: BD = B1D × cos α = d × cos α. B1B = B1D × sin α = d × sin α.
З ΔABD: BD2 = AB2 + AD2, d2 cos2 α = 2а2, 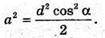
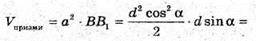
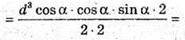
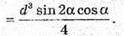
Підставимо у формулу значення d = 37 см, α = 58°.

Відповідь: 6 дм3.
1127.
Знайдемо об’єми кожного з кубів: V1= 13 = 1 см3, V2 = 63 = 216 см3, V3 = 512 см3.
Отже, об’єм трьох переплавлених кубів, а також отриманого куба дорівнює
729 см3. Звідси отримаємо: V = а3, де а – ребро куба, 729 = а3, а – 9 (см).
Відповідь: 9 см.
1128.
Спочатку знайдемо об’єм класної кімнати V: V = 10 × 6 × 3,5 = 210 м3.
Оскільки на кожного учня припадає не менше як 6 м3 повітря, то отримаємо, що
Кімната розрахована на 210 : 6 = 35 (учнів).
Відповідь: 35 учнів.
1129.
Нехай V1 – об’єм паралелепіпеда, V2- об’єм куба, а – ребро куба.
Об’єм паралелепіпеда V1 = 15 × 36 × 50 = 27 000 (дм3).
Об’єм куба V= а3, а3 = 27 000, а = 30 (дм).
Відповідь: 30 дм.
1130.
Нехай а – ребро куба, тоді об’єм V= а3. Збільшимо ребро на 3 см, Отже, ребро куба дорівнює а + 3, тоді об’єм V = (а + 3)3, (а + 3)3 = а3 + 315,
А3 + 9а2 + 27а + 27 = а3 + 513, 9а2 + За – 54 = 0, а2 + 3а – 54 = 0, а = 6 (см). Відповідь: 6 см.
1131.
Нехай ребро першого куба х см, ребро другого куба 3х.
Об’єм першого куба V1 = x3, об’єм другого куба 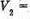
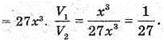
Відповідь: 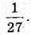
1132.
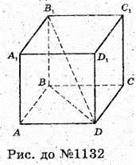
Нехай ABCDA1B1C1D1- прямокутний паралелепіпед,
BB1= 3х, AB = 4х, AD = 12х, B1D = 39 см.
З прямокутного ΔABD: BD2 =AB2 + AD2 = 16х2 + 144×2 = 160×2.
З прямокутного ΔB1BD: B1D2 – B1B2 + BD2, 1521 = 9х2 + + 160×2,
169×2 = 1521, x2 = 9, x = 3.
Отже, отримали: BB1 = 9 (см), AB = 12 (см), AD = 36 (см).
Об’єм V = AB ×AD × BB1 = 9 × 12 × 36 = 3888 (см3).
Відповідь: 3888 см3.
1133.
Нехай x, 2x і 4x – виміри прямокутного паралелепіпеда,
Sповн. = 112 см2. Sповн = 2S oсн. + Sбічн. S oсн. = x × 2x = 2×2;
S бічн. = 2(x + 2x) × 4x = 24×2.
Sповн = 2х2 + 24×2 + 2×2 = 28×2. Отже, маємо: 28×2 = 112 см2, x2 = 4, x = 2.
Звідси маємо виміри прямокутного паралелепіпеда 2, 4 і 8.
Отже, V = 2 × 4 × 8 = 64 (см3).
Відповідь: 64 см3.
1134.
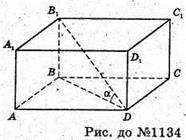
Нехай ABCBA1B1C1B1прямокутний паралелепіпед, у якого AB = a, AB = b, ∠B1BB = а. Об’єм V паралелепіпеда дорівнює V = AB × AD × BB1 =ab × BB1,
З ΔABD: 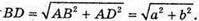
З ΔBB1B: 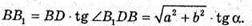
Отже, 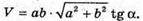
Відповідь: 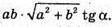
1135.
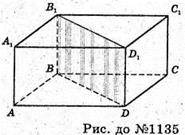
Нехай ABCBA1B1C1B1- прямокутний паралелепіпед, V = 38 дм3.
Діагональна площина ділить прямокутний паралелепіпед на дві рівновеликі призми. Отже, V 1 призми дорівнює: 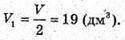
Відповідь: 19 дм3.
1136.
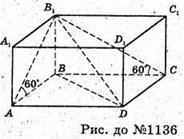
Нехай ABCBA В C1B – прямокутний паралелепіпед. 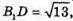
∠B1CB = 30°, ∠B1AB – 60°, BB1 = x.
З ΔAB1B: 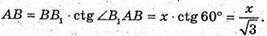
З ΔB1BC: 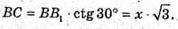
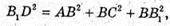
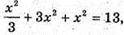
X2+ 9х2 + 3х2 = 39, 13х2 = 39, x2= З, 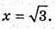
Звідси маємо 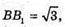
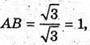
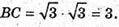
Об’єм 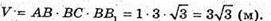
Відповідь: 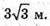
1137.
Нехай ABCBA1B1C1B1- прямокутний паралелепіпед,
B1B = d, ∠B1DB = β. ∠B1BC1 = α.
З ΔB1DB: BB1= B1B sin β = d sin β, BD = B1B cos β = d cos β.
3 ΔB1C1D: BC = B1D sin α = d sin α = BC.
3 ΔBCD: 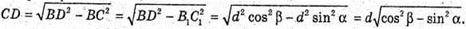
Для об’єму прямокутного паралелепіпеда маємо:
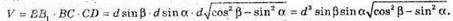
Відповідь: 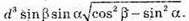
1138.
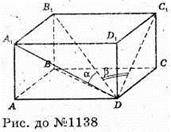
Нехай ABCDA1B1C1D1 – прямокутний паралелепіпед,
B1D = d, ∠B1DA1 = α, ∠B1DC1 = β.
З ΔAB1D: A1B1 = B1D × sin α = d × sin α = АВ.
З ΔB1DC1: B1C1 = B1D × sin β = d sin β = BC.
З ΔB1BD: BD2 = AB2 + BC2 = d2 sin2 α + d2 sin2 β.
3 ΔB1BD: 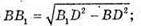
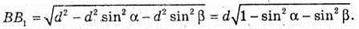
Для об’єму V прямокутного паралелепіпеда маємо:
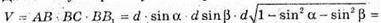
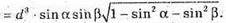
Відповідь: 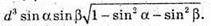
1139.
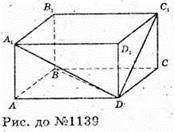
Нехай ABCDA1B1C1D1- прямокутний паралелепіпед,
A1D = 5 см, C1D = = 3 см, 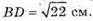 AB = х, BС = у, BB 1 = z.
AB = х, BС = у, BB 1 = z.
З прямокутного ΔABD: BD2 = AB2 + AD2 = x2 + у 2, 22 = x2 + у2.
З AA1AD: A1D2 = AA12 + AD2 = z2 + у2; 25 = z2 + у2.
З AC1CD: C1D2 = C1C2 + CD2 = z2 + x2, 9 = z2 + х2.
Отримаємо систему:
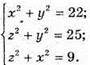
Додавши всі рівняння, отримаємо: 2(x + у2 + z2) = 56; x2 + у2 + z2 = 28,
Тоді з першого рівняння отримаємо: 22 + z2 = 28; z2= 6; 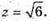
З другого рівняння отримаємо: x2 + 25 = 28; х2 = 3; 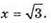
З третього рівняння отримаємо: у2 + 9 = 28; у2 = 19; 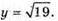
Для об’єму паралелепіпеда V маємо: 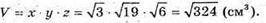
Відповідь: 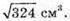
1140.
Нехай ABCDA1B1C1D1 – прямокутний паралелепіпед,
A1D = 5 см, C1D = 8 см, ∠A 1DC 1 = 60°, А1B1 = x, B1C1 = у, ВВ1 = z.
З ΔA1C1D за теоремою косинусів:
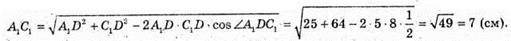
З ΔA1B1C1: 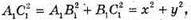 49 = x2 + у2.
49 = x2 + у2.
З ΔA1AD: A1D2 = A1A2 + AD2 = z2 + y2, 20 = z2 + у2.
З ΔC1CD: C1D2 = C1C2 + CD2 = x2 + z2, 64 = х2 + z2.
Отримаємо систему:
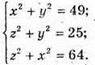
Додавши всі рівняння, отримаємо: 2(х2 + у2 + z2) = 138; х2 + у2 + z2 = 69. Підставимо перше рівняння системи в отримане: 49 + z2 = 69, z2 = 20, Підставимо друге рівняння системи в отримане: х2 + 25 = 69, x2= 44, 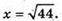
Підставимо третє рівняння системи в отримане: 64 + у2 – 69, у2 = 5,
Для об’єму прямокутного паралелепіпеда маємо: 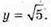
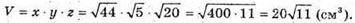
Відповідь: 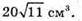
1141.
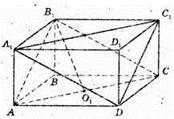
Нехай в прямокутному паралелепіпеді ABCDA1B1C1D1. AB = 3 см, 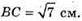
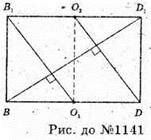
Проведемо площини AB1C і A1C1D і розглянемо переріз паралелепіпеда ABCDA1B1C1D1 площиною BB1D2D. Тоді BD1+ B1O1і BD1 + DO2і BM = 2,4 см.
Оскільки BO1 = O1D і O1M? DK, то за теоремою Фалеса BM = Мk.
Оскільки B1O2 = O2D2 і B1M? O2K, то за теоремою Фалеса MK = KD1.
Тоді BM = MK = KD1, Отже, BD1 = 3 × BM = 3 × 2,4 = 7,2(см).
Оскільки AB2 + BC2 + BB1 = BD12 або 9 + 7 + BB12 = 7,22, то
BB21 = 7,22 – 16 = 51,84 -16 = 35,84, звідси 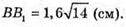
Тоді 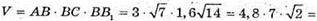
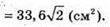
Відповідь: 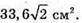
1142.
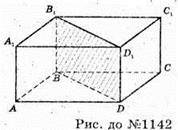
Нехай ABCDA1B1C1D1- прямокутний паралелепіпед,
AB : BC = 5 : 12, PBB1D1D = 78 см.
Позначимо AB = 5x, BC = 12x. ·
З ΔABD за теоремою Піфагора:
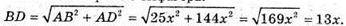
PB1BDD1 = BB1 + B1D1 + D1D + BD = BB1 + BD + BB1 + BD = 2 (BВ1 + BD).
З другої сторони PB1BDD1 = 78 см.
Отже, маємо 2(ВВ 1 + BD) = 78; BB1 + BD = 39;
BB1 = 39 – BD = 39 – 13x.
Тоді V = 60×2(39 – 13x) = 780×2(3 – x).
Знайдемо найбільше значення функції V = 780×2(3 – x), де x? [0; 3].
V′ = (2340×2 – 780×3)′ = 4680x – 2340×2 = 2340x(2 – x).
Знайдемо критичні точки; V′ = 0; 2340x(2 – x) = 0; x = 0 або x = 2.
V(0) = 0; V(2) = 780 × 22 × (3 – 2) = 3120: V(3) = 0.
Отже, 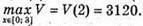
Таким чином, найбільший об’єм прямокутного паралелепіпеда дорівнюватиме 3120 см3.
Відповідь: 3120 см3.
1143.
Нехай ABCDA1B1C1D1- закритий ящик, в якого AB = BC = х.
За умовою задачі S повн = S, тоді 2×2 + 4x × АА 1. = S, звідси 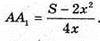
Тоді об’єм ящика 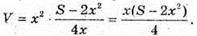
Знайдемо найбільше значення функції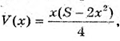
Де x? [0; +∞); 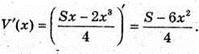
Знайдемо критичні точки функції V(x):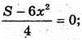 S – 6х2 = 0;
S – 6х2 = 0;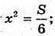
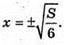
Точка 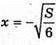 не входить в проміжок x? [0; +∞).
не входить в проміжок x? [0; +∞).
Оскільки 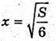 – єдина критична точка на проміжку [0; +∞),
– єдина критична точка на проміжку [0; +∞),
То з’ясуємо зростання (спадання) функції на проміжках 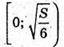
І 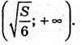 Якщо
Якщо 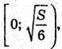 то V(x) > 0; якщо
то V(x) > 0; якщо 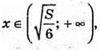 то V′(x) < 0.
то V′(x) < 0.
Отже, точка 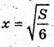 – точка максимуму. Оскільки функція V(x) на проміжку
– точка максимуму. Оскільки функція V(x) на проміжку
[0; +∞) має єдину точку максимуму, то при 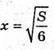 об’єм буде найбільший.
об’єм буде найбільший.
Отже, розміри ящика 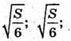
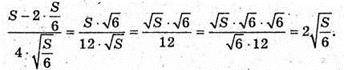
Відповідь: 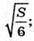
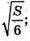
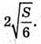
1144.
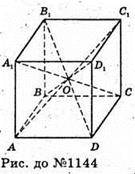
Нехай ABCDA1B1CiD1- куб. Куб ABCDA1B1C1D1 складається з шести пірамід, вершина якої – середина діагоналі куба, а основа – його грань. Оскільки об’єм куба V, то об’єм піраміди дорівнює 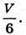
Відповідь: 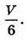
1145.
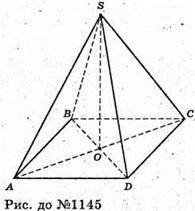
Нехай SABCD – задана піраміда, SO + (ABC), SO = 5 см,
AB = AD = CD = BC = 10 см. Об’єм піраміди V дорівнює:
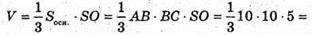
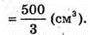
Відповідь: 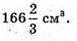
1146.
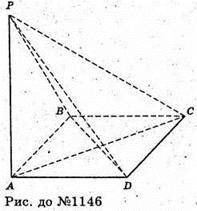
Нехай PABCD – задана піраміда, PA + (ABC), PA = a, AB = BC = CD = AD = а. Об’єм піраміди V дорівнює: 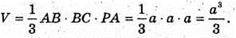
Відповідь: 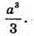
1147.
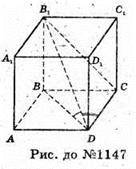
Нехай ABCDA1B1C1D1 – призма. AB = BC = CD = AD = a. ∠B1DB + ∠B1DC = 135.
Нехай ∠B 1DB = α, тоді ∠B1DC = 135° – α.
З ΔABD: 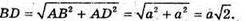
З ΔB1BD: 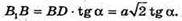
З ΔB1CD: 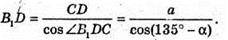
З ΔB1BD: 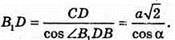
Прирівняємо праві частини: 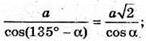
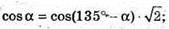
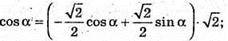 2 cos α = sin α; tg α = 2.
2 cos α = sin α; tg α = 2.
Отже, об’єм V призми дорівнює: 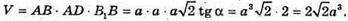
Відповідь: