Поворот і симетрія відносно прямої
373.
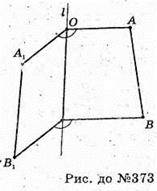
Із т. А опустимо перпендикуляр AD + l. Відкладемо ∠ΑΟΛ, = α, А1O + l.
Виконано поворот т. А навколо прямої l на кут α. Аналогічно вчинимо з т. В.
Відрізок АВ у результаті повороту на кут α навколо прямої l відобразиться у відрізок.
374.
Таких поворотів безліч.
375.
Точка А(1; 2; 0) відобразиться на т. A1 (1; 0; 2).
376.
У результаті повороту відрізок АВ відобразиться на відрізок A1B1,
A1(4; 3; 0), В1(0; 6; 0).
377.
ΔАВС відобразиться на ΔА1В1С1 A1(0; a; 0), B1(-а; 0; 0), С1(0; 0; а)
У результаті повороту
378.
Куб має 7 осей симетрії; прямокутний паралелепіпед, відмінний від куба –
3 осі симетрії.
379.
Якщо n – непарне, осей симетрії немає, якщо n – парне, то вісь симетрії одна, правильний тетраедр має З осі симетрії.
380.
Сфера має безліч осей симетрії. Осі симетрії проходять через центр сфери.
381.
Правильна шестикутна призма має 4 осі симетрії.
382.
Правильна п’ятикутна призма має вісь симетрії.
383.
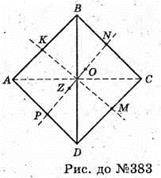
Правильний тетраедр має 3 осі симетрії; пряма КМ, пряма PN; пряма ZO,
Де K – середина АВ; М – середина CD; Р – середина
Z – середи на АС; О – середина BD.
384.
АС – вісь симетрії фігури.
385.
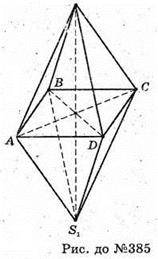
Ця фігура має осі симетрії: SS1; АС; BD.
386.
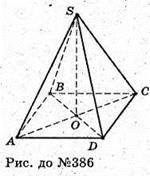
Sabcd – правильна чотирикутна піраміда.
SO – висота. SO – вісь симетрії піраміди.
ΔBSD — рівнобедрений BD + SO; BO = OD.
Отже, у випадку симетрії відносно SO т. В відобразиться у т. D,
Т. S відобразиться сама у себе.
Тоді відрізок SB відобразиться у відрізок SD.
Аналогічно у ΔASC: відрізок SA відобразиться у відрізок SC.
При симетрії відносно SO піраміда відобразиться сама в себе.
Отже, SO – вісь симетрії піраміди.
387.
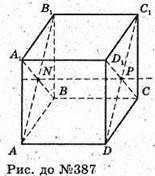
ABCDA1B1C1D1 – паралелепіпед.
N – точка перетину діагоналей грані ΑΑ1Β1Β;
Р – точка перетину діагоналей грані DD1C1C.
МР – вісь симетрії паралелепіпеда ABCDA1B1C1D1, бо:
ΑΒ1C1D – прямокутник, NP – вісь його симетрії, бо:
В1, відобразиться в А, С1- в D.
Аналогічно з прямокутником A1D 1CB.
При симетрії відносно NP паралелепіпед ABCDA1B1C1D1,
Відобразиться в себе.
Отже, NP – вісь симетрії паралелепіпеда.
388.
Середина відрізка АB – точка О1.
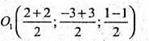Або O1(2; 0; 0) – лежить на осі ОХ
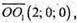
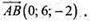
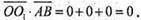
Тому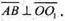 
Отже, АВ перпендикулярний до осі ОХ і віссю ОX ділиться навпіл.
Тому A і В симетричні відносно осі ОХ.
А1 – симетрична А відносно осі OY: А1(-2; -3; – 1).
А2 – симетрична А відносно осі OZ: А2(-2; 3;1).
В1 – симетрична В відносно осі OY: В1(-2; 3; 1).
B2 – симетрична В відносно осі OZ; В2 (-2; -3;-1).
389.
Віссю симетрії двох мимобіжних прямих є спільний перпендикуляр.
390.
А) Віссю симетрії фігури, яка є об’єднанням двох прямих,
Що містять ребра AA1 і CD, є їх спільний перпендикуляр AD.
Б) Віссю симетрії фігури, яка є об’єднанням двох прямих,
Що містять ребра ВВ1 і АС, є пряма BD.
В) Віссю симетрії фігури, яка є об’єднанням прямих,
Що містять АВ1 і CD1, є пряма KM, K – середина АВ1, М – середина DC.
391.
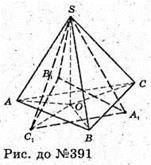
SABC — правильна трикутна піраміда. SO – висота.
При повороті SABC навколо SO на 180° піраміда SABC
Відобразиться в піраміду SA1B1C1.
392.
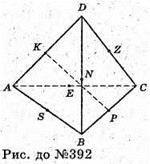
ABCD – тетраедр, у якого АВ = DC; ВС = AD; АС = BD.
K – середина AD; Р – середина ВС; КР – вісь симетрії тетраедра.
При симетрії відносно KР т. С відобразиться в т. В; т. D відобразиться в т. А.
Таким чином ΔАОС відобразиться в ADAB, а тетраедр ABCD відобразиться
Сам у себе. Таких осей симетрії 3: КР; SZ; NE.
393.
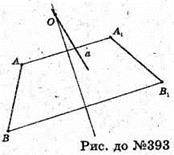
А – серединний перпендикуляр до АА 1; b – серединний перпендикуляр до BB1;
А і b перетинаються в т. О.
Поворот навколо т. О на ∠ΑΟΑ, або на кут 360° – ∠ΑOΑ1
Відобразить АВ на A1B1.
Можна провести серединні перпендикуляри до відрізків
АВ1 і A 1В аналогічно (вищевказаному способу).
394.
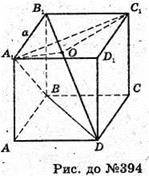
AО + B1D; С1О + B1D.
При повороті куба на кут А1ОС, навколо прямої Β1D куб відобразиться сам в себе.
Із ΔA1B1D – прямокутного, у якого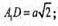 
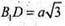
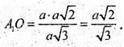
Аналогічно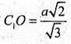 
(із ΔA 1C1D).
Розглянемо ΔA ОС1: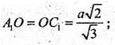 
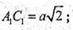
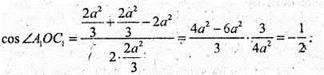
Тоді ∠A 1OC 1 = 120°. 120° = 360° : 3. Отже, B1D – вісь симетрії третього порядку.
Таких осей 4: Β1D; BD1; А1С; АС1.
395.
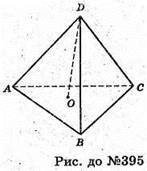
При повороті навколо DO на ∠ΑΟΒ тетраедр ABCD відобразиться сам в себе.
∠AОВ = 360° : 3, тому DО – вісь симетрії третього порядку.
396.
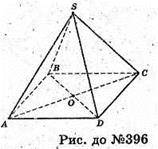
Правильна чотирикутна піраміда не має осі симетрії третього порядку,
Бо не існує такого повороту (на 120°), щоб піраміда відобразилась сама в себе.
398.
А)
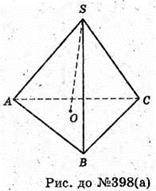
Повороти навколо висоти SO на ±120°; ±240°; ±360° відобразять піраміду
SABCD саму на себе;
Б)
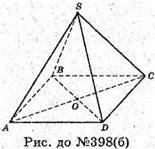
Повороти навколо висоти SO на ± 0°; ±180°; ±270° відобразять піраміду
SABC саму у себе;
В)
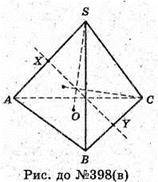
Повороти навколо висот SO; CK; AN; ВР на ±120°; ±240°; +360° відобразять
Тетраедр сам у себе.
Також повороти навколо прямих, що проходять через середини протилежних
Ребер (наприклад XY) на ±180° відобразять тетраедр у себе.
399.
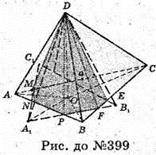
При повороті тетраедра ABCD навколо висоти DO на 60° тетраедр відобразиться
На тетраедр A1Β1C1D1. Перерізом цих тетраедрів є піраміда DMNPFEQ.
Фігура, зафарбована кольором, є об’єднанням цих тетраедрів.
400.
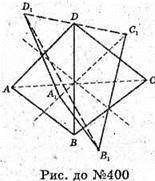
Див. рис.
401.
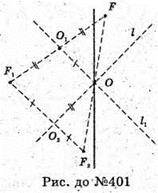
Нехай l і l1 – дві перпендикулярні осі симетрії, які перетинаються.
F – точка деякої фігури. При симетрії відносно l1 т. F перейде в т. F1,
А відносно l т. F1 перейде в т. F2. ΔFO1O = ΔF2O2O, тому т. F може
Перейти т. F2 відносно т. О, або відносно прямої l2, яка перпендикулярна площині, проведеній через І і l1, і проходить через т. О.
(1 votes, average: 5.00 out of 5)
Loading...