Прийоми усного множення і ділення в межах 1000

Мета: узагальнити й систематизувати уміння виконувати прийоми усного позатабличного множення та ділення.
Дидактичні задачі. Актуалізувати уміння виконувати прийоми усного множення і ділення в межах 1000: множення та ділення на одноцифрове число; множення та ділення круглих чисел на одноцифрове способом укрупнення розрядних одиниць, способом множення ( ділення) добутку на число ; ділення на кругле число способом укрупнення розрядних одиниць; способом послідовного ділення; ділення на двоцифрове число способом
Розвивальна задача: розвивати логічне мислення учнів (с. 25 №1).
ХІД УРОКУ
І. МОТИВАЦІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ
Схвалюючи певне рішення, доросла людина має розглянути різні варіанти розв’язування певної ситуації, визначити найбільш раціональний. Тому, щоб підготуватися до дорослих справ, сьогодні на уроці ми продовжимо досліджувати різні способи міркування при знаходженні значень виразів – добутків та часток. Для цього ми пригадаємо суть прийомів обчислення та вдосконалимо уміння виконувати усне множення та ділення в межах 1000. Отже, готуємось
ІІ. УЗАГАЛЬНЕННЯ Й СИСТЕМАТИЗАЦІЯ ВИВЧЕНОГО
1.Математичний диктант.
1) Число 370 зменшити на 80.
2) Знайти суму 560 і 170.
3) Знайти добуток чисел 46 і 5.
4) Знайти частку чисел 200 і 25.
5) Зменшуване 420, значення різниці 240. Знайти від’ємник.
6) Другий доданок 240, значення суми 320. Знайти перший доданок.
7) Знайти зменшуване, якщо від’ємник 170, а значення різниці 440.
8) Знайти ділене, якщо значення частки 30, а дільник 8.
9) Перший множник 50. Знайти другий множник, якщо значення добутку 300.
10) Ділене 510, а значення частки 3. Знайти дільник.
11) Скільки можна купити ручок на 260 гривень, якщо ціна кодної становить 5 гривень?
12) Майстер має виготовити 480 деталей за 8 робочих годин. По скільки деталей він має виготовляти щогодини?
13) Маса коробки печива 800 г. Яка маса 3 таких самих коробок?
2.Узагальнення прийомів позатабличного множення та ділення.
Завдання №1 виконується колективно.
Пропонуємо учням прокоментувати знаходження значення добутку 56 і 6 ( 1) Перший множник замінюємо сумою розрядних доданків; 2) множимо суму на число, для цього кожний доданок множимо на число та одержані добутки додаємо) . Зіставляємо другий добуток з першим: змінився перший множник до нього ліворуч дописали ще одну цифру і одержали трицифрове число. З’ясовуємо, як ця зміна вплине на розв’язання: оскільки перший множник трицифрове число, то замінюючи його сумою розрядних доданків одержимо три доданки, які ми будемо множити на число. Висновок: при множенні двоцифрового або трицифрового числа на одноцифрове, треба двоцифрове або трицифрове число замінити сумою розрядних доданків і помножити цю суму на число. Отже, теоретичною основою множення двоцифрового або трицифрового числа на одноцифрове є правило множення суми на число. Учні формулюють його.
Зіставляємо добуток 56 і 6 та частку 56 і 4. З’ясовуємо, чи можна міркувати аналогічно при діленні двоцифрового числа на одноцифрове. Так, треба двоцифрове ділене замінити сумою не розрядних, а зручних, доданків, і потім суму поділити на число. Далі міркування аналогічні до знаходження добутку чисел 56 і 6. Визначаємо, що основою цього прийому обчислення є правило ділення суми на число. Учні формулюють його.
Зіставляємо другу частку з першою: змінилося ділене. З’ясовуємо, як вплине зміна діленого на спосіб розв’язування. Жодним чином не вплине: ділене замінюємо сумою зручних доданків і ділимо суму на число. Можна запропонувати учням зіставити міркування при множенні трицифрового числа на одноцифрове та при діленні трицифрового числа на одноцифрове: при множенні ми трицифрове число замінюємо сумою розрядних доданків, а при діленні – сумою зручних доданків; при множенні ми трицифрове число замінили сумою трьох доданків, а при діленні – двох. Обговорюємо питання: чи можна при діленні замінити трицифрове ділене сумою трьох доданків (так, можна, наприклад 100, 40 і 16, але це ускладнить обчислення.). Узагальнюємо: як треба міркувати при діленні двоцифрового та трицифрового числа на одноцифрове; при множенні та ділення двоцифрового та трицифрового числа на одноцифрове ( 1) замінюємо двоцифрове або трицифрове число сумою розрядних чи зручних доданків; 2) множимо або ділимо суму на число).
Завдання №1 із зошита з друкованою основою виконується з коментарем.
Завдання №2 виконується колективно.
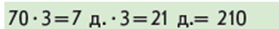
Використано спосіб укрупнення розрядних одиниць: 1) замінюємо кругле число більшими розрядними одиницями – десятками; 2) множимо число десятків на одноцифрове число, одержуємо десятки; 3) результат подаємо у одиницях.
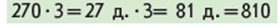
Зіставляємо цей випадок обчислення з попереднім: до першого множника дописали ліворуч одну цифру й одержали трицифрове число. З’ясовуємо, як зміна першого множника вплине на розв’язання: міркування не зміняться, лише при заміні першого множника десятками, одержимо двоцифрове число десятків, і треба буде двоцифрове число множити на одноцифрове. Учні коментують подане розв’язання. Отже, в обох випадках застосовано прийом укрупнення розрядних одиниць, який дозволяє будь-яке кругле число помножити на одноцифрове число.
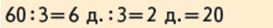
Чи використати прийом укрупнення розрядних одиниць при діленні круглого числа на одноцифрове? Міркування аналогічні до множення.
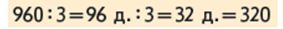
Зіставляємо частки. Що мінилося? Як ця зміна вплине на розв’язання? Узагальнюємо спосіб міркування при діленні круглого числа на одноцифрове. Узагальнюємо спосіб міркування при множенні та діленні будь-якого круглого числа на одноцифрове число.
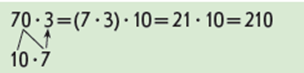
Пропонуємо учням прокоментувати обчислення значення добутку 70 і 3 іншим способом – способом на підставі правила множення добутку на число: 1) перший множник – кругле число подаємо у вигляді добутку числа та розрядної одиниці; 2) множимо добуток на число: для цього достатньо помножити одноцифрове число на один з множників – перемножуємо числа, а потім результат множимо на інший множник – на розрядну одиницю. З’ясовуємо, що є теоретичною основою цього прийому обчислення. Учні формулюють правило множення добутку на число.
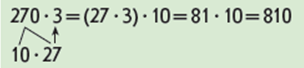
З’ясовуємо, чи можна так само міркувати при множенні круглого трицифрового числа на одноцифрове. Учні коментують подане розв’язання. З’ясовуємо відмінності: ми мали двоцифрове число множити на одноцифрове. Узагальнюємо прийом множення на підставі правила множення числа на добуток для випадків множення будь-якого круглого числа на одноцифрове.
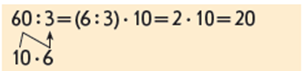
З’ясовуємо, чи можна міркувати аналогічно при діленні круглого числа на одноцифрове. Так, треба буде не множити, а ділити добуток на число; для цього достатньо один з множників розділити на число і помножити результат на інший множник – на розрядну одиницю.
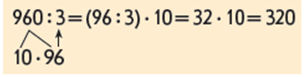
З’ясовуємо, чи можна у такий спосіб розділити кругле трицифрове число на одноцифрове. Учні коментують подане розв’язання. Узагальнюємо прийом ділення на підставі правила ділення добутку на число при діленні будь-якого круглого числа на одноцифрове. Узагальнюємо прийоми множення та ділення на підставі правил множення добутку на число або ділення добутку на число при множенні або діленні будь-якого круглого числа на одноцифрове.
Завдання №2 із робочого зошита виконується з коментарем.
Учні визначають, який спосіб міркування для них є найбільш зручним.
Завдання №3 виконується колективно.
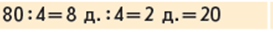
Учні коментують розв’язання способом укрупнення розрядних одиниць.

Зіставляємо частки: що змінилося? Як ця зміна вплине на розв’язання? Тут обидва числа круглі, тому кожне з них можна замінити однаковими більшими розрядними одиницями – десятками; розділити числа десятків та в результаті одержуємо число без найменування.
Зіставляємо:
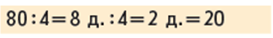 і
і 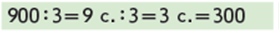
У чому відмінність? Як вона вплине на розв’язання? Узагальнюємо спосіб укрупнення розрядних одиниць при ділення круглого числа (десятків та сотень) на одноцифрове число.
Зіставляємо:
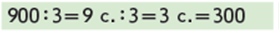 і
і 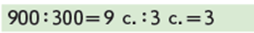
Узагальнюємо прийом укрупнення розрядних одиниць при діленні: 1) замінюю ділене ( ділене та дільник) більшими розрядними одиницями (однаковими) – десятками або сотнями; 2) виконуємо ділення числа розрядних одиниць на одноцифрове ( чисел, поданих у певних розрядних одиницях); 3) одержане число розрядних одиниць подаю в одиницях ( одержано число без найменування).
Спробуємо застосувати узагальнений алгоритм прийму укрупнення розрядних одиниць для обчислень. Учні пояснюють розв’язання:
 та
та 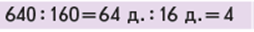
Зіставляємо розв’язання:

Застосовані різні прийоми обчислення: прийом укрупнення розрядних одиниць та прийом на підставі правила ділення добутку на число.
Чому 80 замінили добутком числа та розрядної одиниці? ( Тому що будь-яке кругле число можна замінити добутком числа та розрядної одиниці.) З’ясовуємо, чи можна міркувати у такий спосіб – замінивши дільник – кругле число – добутком числа та розрядної одиниці:

У цьому випадку обчислення змінилася теоретична основа – обчислення виконуються на підставі правила ділення числа на добуток. Щоб розділити число на добуток, достатньо це число розділити на один множник – на розрядну одиницю, а потім одержаний результат розділити на інший множник – на число.
Зіставляємо розв’язання:
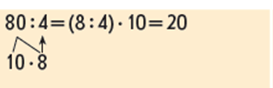 І
І 
Узагальнюємо: при діленні на одноцифрове число ділене замінюють добутком числа та розрядної одиниці, а при діленні на кругле число – дільник замінюють добутком числа та розрядної одиниці. При діленні на одноцифрове число дії виконуються на підставі правила ділення добутку на число; а при діленні на кругле число – на підставі правила ділення числа на добуток. Учні формулюють правила.
К можна міркувати при обчисленні значення частки. Учні коментують подане розв’язання.
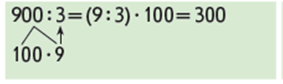
На підставі якого правила відбувається обчислення?
Зіставляємо розв’язання і узагальнюємо спосіб міркування:
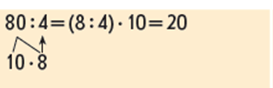
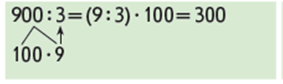
Чи можна міркувати так само при діленні? Застосовуємо узагальнений алгоритм для наступного випадку обчислення.

Учні зіставляють розв’язання і узагальнюють спосіб міркування.
 і
і 
Чи можна міркувати так само при діленні? Застосовуємо узагальнений алгоритм для коментування наступного випадку обчислення.

Завдання №3 із робочого зошита виконується з коментарем.
Завдання №5 пропонуємо для самостійної роботи учнів.
Завдання №6 виконується колективно.

Коментар аналогічний тому, що подано в №3 на с. 6 підручника. Застосовано прийом на підставі конкретного змісту дії ділення – прийом добору.

Зіставляємо цю частку з попередньою. З’ясовуємо, у чому відмінність: і ділене, і дільник – круглі числа. Чи допоможе перше розв’язання знайти значення даної частки? Щоб знайти значення цієї частки добором, треба замінити і ділене і дільник однаковими більшими розрядними одиницями – десятками, і у такий спосіб звести цей випадок обчислення до попереднього.
Учні коментують розв’язання.
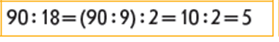
Застосовано прийом ділення числа на добуток: 1) двоцифровий дільник замінюю добутком зручних множників; 2) ділю число на добуток: спочатку ділю ділене на один з множників, а потім одержаний результат ділю на інший множник.
Чи допоможе попереднє розв’язання для обчислення значення частки?
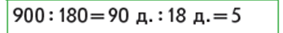
Так, замінивши і ділене і дільник однаковими більшими розрядними одиницями – десятками, призведемо обчислення до попереднього випадку. Звертаємо увагу на те, що при діленні десятків на десятки одержуємо число без найменування.
Завдання №7 виконується учнями з коментарем.
3.Розвиток логічного мислення учнів.
С. 25 Завдання №1 – колективна робота з класом ( у підручнику подано готове розв’язання).
УІІ. ПОЯСНЕННЯ ЗАВДАННЯ ДЛЯ ДОМАШНЬОЇ РОБОТИ
Завдання №5 та №7 передбачають знаходження значень виразів. Очевидно, що для знаходження значень виразів можна застосувати не один прийом обчислення. Учням пропонується вибрати для себе найбільш зручний.
УІІ. ПІДСУМОК. РЕФЛЕКСІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ
Які прийоми множення ви сьогодні узагальнили? Чим відрізняється процес множення двоцифрового числа на одноцифрове від множення трицифрового числа на одноцифрове? Що спільне у множенні та діленні на одноцифрове число; що відмінне? У яких випадках застосовується прийом укрупнення розрядних одиниць при множенні та діленні? Які прийоми обчислення можна застосувати при множенні та діленні круглого числа на одноцифрове? Як можна міркувати при діленні круглого числа на кругле? Розкажіть про результати власних навчальних досягнень: Я розпізнаю… Я знаю… Я розумію… Я можу пояснити… Я вмію… Мені цікаво… В мене добре виходить… Мені ще слід попрацювати над…