Рівняння. Нерівності зі змінною
Рівняння. Нерівності зі змінною
1
Розбий записи на дві групи. Назви кожну групу.
27 + х = 51 27 + х < 51 40 ∙ р > 160
2
Згадай, що ти знаєш про рівняння; про нерівності зі змінною. Розглянь, як учні розв’язали рівняння та нерівність способом добору. Прокоментуй їхні дії. Із чисел 1, 2, 4, 6, 12, 18 вибери ті, що є розв’язком рівняння; розв’язком нерівності.
36 : х = 18
Х = 1,
36 : 1 = 18 – хибно;
Х = 2,
36 : 2 = 18 – істинно.
Відповідь: 2.
А – 8 > 4
Слід почати випробування з числа, яке більше за 8, тому що не вміємо від меншого
А = 12,
12 – 8 > 4 – хибно;
А = 18,
18 – 8 > 4 – істинно.
Відповідь: 18.
3
Перевір розв’язання, виконані учнями. Які способи розв’язання застосовано?
Раціональний спосіб добору розв’язків нерівності
36 : х = 18
Х = 36 : 18
Х = 2
36 : 2 = 18
18 = 18
Відповідь: 2.
А – 8 > 4
1) а – 8 = 4
А = 4 + 8
А = 12

11 – 8 > 4 – хибно.
3) Відповідь: 13, 14, 15…
4
Перевір, як розв’язано рівняння на основі властивостей рівності. Розв’яжи подані рівняння зручним для тебе способом.
36 : х = 18
36 : х = 36 : 2
Х = 2
Відповідь:
А ∙ 9 = 99
53 : b = 17
Р : 19 = 38
K + 23 = 60
– Розв’язок, корінь рівняння
– Розв’язки нерівності зі змінною
5
Розглянь, як учні розв’язали нерівності на основі залежності результату арифметичної дії від зміни одного з компонентів. Прокоментуй розв’язання.
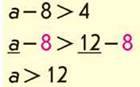
Із двох різниць з однаковими від’ємниками більша та, в якій зменшуване більше.
Відповідь: 13, 14, 15 …
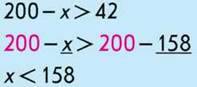
Відповідь: 0; 1; 2; 3; 4 … 157.
Найбільше значення х, за якого нерівність буде істинною, – це число 157.
6
У кожному стовпчику розв’яжи перше рівняння. Як можна друге рівняння у стовпчику звести до першого? Розв’яжи друге рівняння.
42 – k = 18 b + 26 = 70 n ∙ 6 = 54
42 – k = 72 : 4 b + 13 ∙ 2 = 70 n ∙ 6 = 540 : 10
7
Знайди деякі розв’язки кожної нерівності.
36 – а < 9 р + 26 < 50 k – 27 > 18
8
□ На екскурсію поїхали 28 хлопчиків, а решта – дівчатка. Усі вони розмістились у двох автобусах, по 25 учнів у кожному автобусі. Скільки дівчаток поїхало на екскурсію?
Прокоментуй розв’язання задачі алгебраїчним методом.
Х – кількість дівчаток.

Маємо: 28 + х = 25 ∙ 2.
28 + х = 25 ∙ 2
28 + х = 50
Х = 50 – 28
Х = 22
Відповідь: 22 дівчинки.