Головна ⇒ 📌Математика ⇒ РІВНЯННЯ. ОСНОВНІ ВЛАСТИВОСТІ РІВНЯНЬ

РІВНЯННЯ. ОСНОВНІ ВЛАСТИВОСТІ РІВНЯНЬ

Розділ 5 ВИРАЗИ І РІВНЯННЯ

§ 31. РІВНЯННЯ. ОСНОВНІ ВЛАСТИВОСТІ РІВНЯНЬ

Ви вже знаете, що таке рівняння, корінь рівняння. Пригадаємо основні формулювання.

Запам’ятайте

Рівнянням називається рівність, що містить невідоме, значення якого треба знайти.

Невідоме число в рівнянні позначають буквою х, або у, або z тощо. Наприклад, запис 4х + 7 = 15 є рівнянням, де х – невідоме і є шуканим.

Значення невідомого, за якого рівняння перетворюється на правильну числову рівність, називається коренем рівняння.

Так, коренем рівняння

4х + 7 = 15 є число 2, бо 4-2 + 7 = 15.

Рівняння може мати більше, ніж один корінь. Наприклад, рівняння 0 ∙ х = 0 має безліч коренів, оскільки будь-яке число перетворюе рівняння на правильну числову рівність. З рівняннями, які мають два, три або більше коренів, ви зустрінетеся пізніше.

Рівняння може не мати коренів. Наприклад, рівняння 0 ∙ х = -12 не має коренів, бо не існує числа, яке в добутку з числом 0 дає число -12.

Розв’язати рівняння – означає знайти всі його корені або встановити, що рівняння не має жодного кореня.

У 5 класі ви ознайомились із найпростішими рівняннями. Розв’язуючи їх, ви знаходили корінь рівняння

як невідомий компонент арифметичної дії. Під час розв’язування складніших рівнянь спираються на властивості рівностей. Розглянемо основні з них.

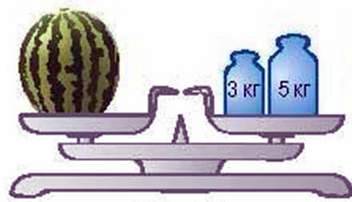
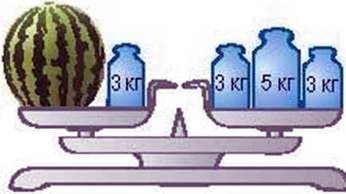
Поди віт вся на малюнок 139. Ви бачите, що на лівій шальці терезів розміщується кавун невідомої маси, а на правій – гирі масою 5 кг і 3 кг. Якщо на обидві шальки терезів покласти по гирі масою З кг, то терези залишаться в рівновазі (мал. 140). Зрозуміло, що, знявши ці гирі або поставивши на терези однакові гирі іншої маси, знову дістанемо рівновагу на терезах. Цей приклад ілюструє таку властивість рівностей.

Запам’ятайте!

Якщо до обох частин рівності додати (від обох частин рівності відняти) одне й те саме число, то рівність не зміниться.

Мал. 139

Мал. 140

Задача 1. Розв’яжіть рівняння: х – 12 = 20.

Розв’язання. До лівої і правої частий рівняння додамо число 12 і спростимо отриману рівність:

Х -12 = 20, х-12 + 12 = 20 + 12, х= 20 + 12, х= 32.

Розв’язуючи рівняння, у лівій його частині “усамітнили невідоме”. Такий самий результат отримаємо, якщо число 1 2 перенесемо з лівої частини у праву, змінивши при цьому його знак.

Запам’ятайте!

Доданок можна переносити з однієї частини рівняння в іншу, змінюючи знак цього доданка на протилежний.

? Чи можна переносити до іншої частини рівняння доданок, що містить невідоме? Так.

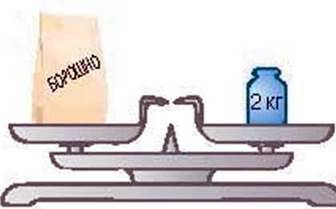
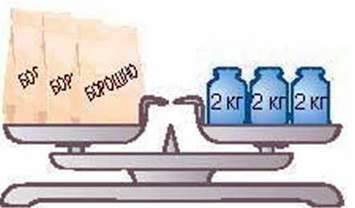
Подивіться на малюнок 141. Ви бачите, що маса пакета борошна дорівнює 2 кг. Зрозуміло, що маса трьох таких пакетів утричі більша (мал.142). Цей приклад ілюструє іншу властивість рівностей.

Запам’ятайте!

Якщо обидві частини рівності помножити (поділити) на одно й то само число, відмінно від нуля, то рівність не зміниться.

Мал. 141

Мал. 142

Наведену властивіств використовують для розв’язування рівнянь. Розглянемо приклад.

Задача 9 Розв’яжіть рівняння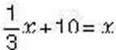

Розв’язання. Щоб позбутися дробового коефіцієнта, помножимо на 3 обидві частини рівняння:

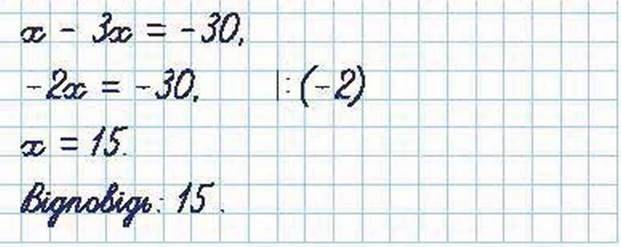
Запам’ятайте!

Основні властивості рівнянь

1. Корені рівняння не зміняться, якщо до обох частин рівняння додати (від обох частин рівняння відняти) одне й те саме число.

2. Корені рівняння не зміняться, якщо обидві частини рівняння помножити (поділити) на одне й те саме число, відмінне від нуля.

Дізнайтеся більше

Вважають, що мова алгебри – це рівняння. “Щоб розв’язати питання, які відносяться до чисел або до абстрактних відношень величин, потрібно лише перекласти задачу з рідної мови на мову алгебраїчну”, – писав великий І. Ньютон (1643-1727) у своєму підручнику з алгебри, названому “Загальна арифметика”.

ПРИГАДАЙТЕ ГОЛОВНЕ

1. Що таке рівняння? корінь рівняння?

2. Що означає “розв’язати рівняння”?

3. Скільки коренів може мати рівняння?

4. Сформулюйте основні властивості рівнянь.

РОЗВ’ЯЖІТЬ ЗАДАЧІ

1408′. Який із записів є рівнянням:

1)14-4 = 56; 2) 5х – 10=0; 3) у + 7 > 21; 4)15 = 4z + 1? Відповідь поясніть.

1409′. Петрик стверджує, що коренем рівняння є число, підстановка якого в рівняння перетворює його на рівність. Чи правий Петрик?

1410′. Скільки коренів може мати рівняння? Наведіть приклад рівняння, яке: 1) не має коренів; 2) має безліч коренів.

1411′. Чи на будь-яке число можна помножити обидві частини рівняння під час розв’язування? А поділити? Відповідь поясніть.

1412°. Чиє число 3 коренем рівняння:

1) 2х-6 = 0; 3)3х – 1 =5;

2) 5y+15 = 0; 4)4х = 9 + х?

1413°. Чи правильно, що число 0 є коренем рівняння:

1)-6x = 0; 3)5х = 0;

2)0: у = -25; 4)1,2:у=0?

1414°. Назвіть кроки розв’язування рівняння:

1) 2х + 10 = -3х; 3) 5х + 4=-2х – 10;

2)-4y-5 = 3; 4) 12-3у=8 + у.

Які властивості рівнянь ви при цьому використовували?

1415°. Розв’яжіть рівняння:

1) 9x-16 = 2; 7) 5х + 4 = 3х-12;

2) 4- 2у = 24; 8)-у + 25= 12y – 1;

3) бх-32- 2х; 9) 10 = 4z-2-2z;

4) -2у-4у + 24; 10)-2 = 3х+ 14+ х;

5)3х-8 = х; 11)10y +6=12y – 8;

6)-20 = 4y+8; 12) 11z-3 = -3 – 12z.

1416°. Розв’яжіть рівняння:

1) 5x – 16 = 14; 4) 12 – y=2y + 6;

2) 8y= 10 + Зу; 5) 3х + 3 = 27 – 5х;

3) 2x -16 = 8+ 12х; 6)-3y-8 = 2у + 7.

1417°. Знайдіть корінь рівняння:

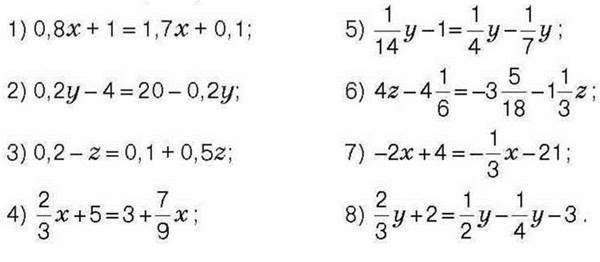
1418. Обчисліть:

1) 1,1 -0,1 z = -1,9-0,7z; 2)-0,2х + 4=-2 + 0,1x;

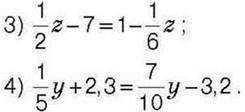
1419°. Складіть рівняння, що містить невідоме в обох частинах, коренем якого є число: 1) 8; 2) 14.

1420°. Складіть рівняння, що містить невідоме в обох частинах, коренем якого є число: 1) 5; 2) 9.

1421. Розв’яжіть рівняння:

1) 5(x – 4) = 3x – 10; 7) 12 – 5(x + 1)=7 + 3x – 2x;

2) 4y + 2 = 3(10- у); 8) -0,2(3 – у) + 1,2 = -0,2(y – 1);

3) 7(x-4) = 5(x + 4); 9) 1-4z-3(1 – z) =-5(z + 2);

4) 3(y + 1) = 6(1 – у) + 6; 10) (18-x)-7(2x-4) = 5x+ 20;

5) 2(x-3)-3(4 – x) = 5; 11) 3(0,4y+3)-0,6y= 8;

6) 7 + 4(3 – у) = 5(у + 2); 12) 2(2 + x) + (4x – 1) ∙ 3 = 10x – 7.

1422. Розв’яжіть рівняння:

1) 7(x + 2) = -14; 4) 7(x + 3) – 2(x – 5) = 8;

2) 8y = 2(5 – у): 5) 5 + 3(2у – 1) = 2(у – 3);

3) 2(3x – 4) = 4(x – 3); 6) – x – 5,2 = 12 – 2(x + 0,6) – 10.

1423. Знайдіть корінь рівняння:

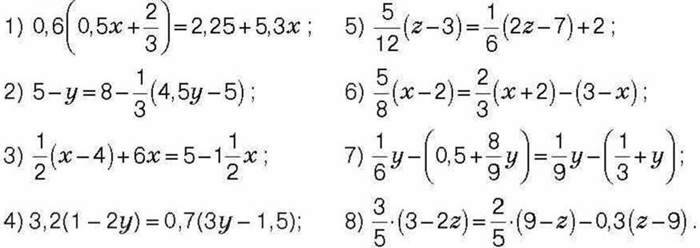
1424. Знайдіть корінь рівняння:

1425. Розв’яжіть рівняння:

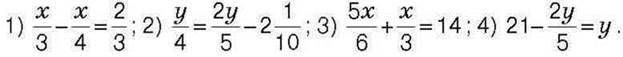
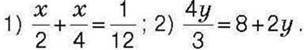
1427. Знайдіть корінь рівняння:

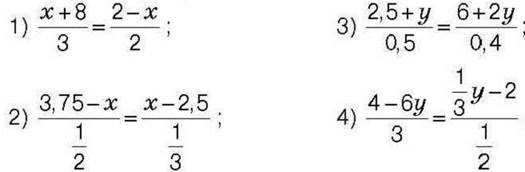
1428. Знайдіть корінь рівняння:

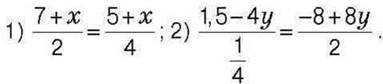
1429*. Якими можуть бути значення х і у, якщо:

1) х + 3у= 11 і 2x + 3у =13; 2) х + у – 18 і х-у – 6?

1430*. Розв’яжіть рівняння:

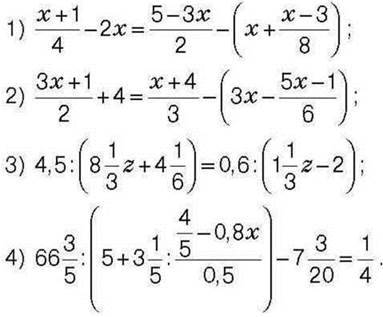
1431*. Дано рівняння:

1)х+2-а; 4)3(x-2) = 2 х-а;

2)5х-а=10; 5) 12-5x = 8(а + 4x);

3) 4(х + 2) = а + 8; 6)7х-2(а-6) = 5х-2.

Знайдіть: а) х, якщо а = 3; б) а, якщо х= 1.

ЗАСТОСУЙТЕ НА ПРАКТИЦІ

1432. Тарасик демонструє друзям математичний фокус “Відгадай дату народження”. Він пропонує одному з них подумки виконати дії: 1) день свого народження помножити на два; 2) до результату додати 5; 3) отриманий результат помножити на 50; 4) додати номер місяця, у якому той народився. Потім просить на-

Звати число. Після цього Тарасик віднімає від отриманого числа 250. У нього виходить чотирицифрове або трицифрове число: перші дві або одна цифра – день народження однокласника, а дві останні – місяць його народження. У чому полягає секрет фокуса?

1433. Придумайте свій математичний фокус.

ЗАДАЧІ НА ПОВТОРЕННЯ

1434. Обчислітьусно значення виразу 12b-7b-4b-9b, якщо:

1) b= 0,8; 2)b = -20.

1435. Довжина садової ділянки прямокутної форми дорівнює 75 м, а ширина становить 0,3 довжини. Знайдіть довжину паркану, що обгороджує цю ділянку.