РІВНЯННЯ. ВЛАСТИВОСТІ РІВНОСИЛЬНОСТІ РІВНЯНЬ
РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ
У розділі дізнаєтесь:
► які рівняння називають рівносильними;
► про властивості рівносильності рівнянь;
► що таке лінійне рівняння з однією змінною;
► які особливості лінійного рівняння з двома змінними;
► про графік лінійного рівняння із двома змінними;
► що таке система двох лінійних рівнянь із двома змінними;
► якими способами розв’язують системи рівнянь;
► як застосувати вивчений матеріал на практиці

&19. РІВНЯННЯ. ВЛАСТИВОСТІ РІВНОСИЛЬНОСТІ РІВНЯНЬ
Ви вже знаєте, що таке вираз зі змінними та як знайти його значення для заданих значень змінних. На практиці доводиться складати ще й рівності зі змінними. Розглянемо приклад.
У пішому поході туристи, як правило, щогодини долають на 0,5 км менше, ніж за попередню годину. Нехай за першу годину туристи проходять х км, тоді за три години разом вони подолають відстань х + (x – 0,5) + (х – 1) км. Відстань х може бути різною для різних груп туристів, оскільки залежить від натренованості учасників походу. Тому отриманий вираз є виразом зі змінною. Нехай відстань, яку подолають туристи за 3 год,
Х + (х – 0,5) + (х – 1) = 13,5.
Дістали рівність зі змінною.
? Чи є отримана рівність рівнянням? Ні. Але ця рівність може набути смислу рівняння, якщо поставити вимогу знайти значення змінної, що перетворює дану рівність зі змінною на правильну числову рівність.
Запам’ятайте!
Рівнянням називається рівність зі змінною, значення якої треба знайти.
Значення змінної, яке перетворює рівняння на правильну числову рівність, називають коренем рівняння.
Наприклад, коренем рівняння х + (х – 0,5) + (х – 1) = 13,5 є число 5, оскільки 5 + (5 – 0,5) + (5 – 1) = 13,5. Інакше кажуть: “Число 5 задовольняє рівняння”.
Рівняння може мати більше, ніж один корінь. Наприклад, у рівнянні (х – 5)(х + 3) = 0 – два корені. Це числа 5 і -3, оскільки (5 – 5)(5 + 3) = 0 і (-3 – 5)(-3 + 3) = 0. А в рівнянні х – х = 0 – безліч коренів, оскільки будь-яке число задовольняє це рівняння.
Зверніть увагу:
Скільки б коренів не мало рівняння, кожен його корінь задовольняє це рівняння.
Рівняння може не мати коренів. Наприклад, у рівнянні 0 ∙ х = -12 немає коренів, бо не існує числа, яке в добутку з числом 0 дає число -12.
Запам’ятайте!
Розв’язати рівняння – означає знайти всі його корені або встановити, що рівняння не має жодного кореня.
Рівняння, які мають одні й ті самі корені, називають рівносильними. Наприклад, рівняння 2(х – 6) + 10 = 12 і 2х = 14 є рівносильними, оскільки і перше, і друге рівняння мають один корінь і цей корінь – число 7. Рівняння, які не мають коренів, також вважають рівносильними.
Під час розв’язування рівнянь використовують такі властивості.
Запам’ятайте!
Властивості рівносильності рівнянь
1. Якщо до обох частин рівняння додати одне й те саме число, то отримаємо рівняння, рівносильне даному.
2. Якщо в рівнянні перенести доданок із однієї частини в іншу, змінивши при цьому його знак на протилежний, то отримаємо рівняння, рівносильне даному.
3. Якщо обидві частини рівняння помножити або поділити на одне й те саме число, відмінне від нуля, то отримаємо рівняння, рівносильне даному.
4. Якщо перше рівняння рівносильне другому, то друге рівняння рівносильне першому.
5. Якщо перше рівняння рівносильне другому, а друге – третьому, то перше рівняння рівносильне третьому.
Задача. Розвяжіть рівняння  – 7 = 1 –
– 7 = 1 – 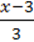 .
.
Розв’язання. Застосуємо властивості рівносильності рівнянь і тотожні перетворення. Обидві частини рівняння помножимо на 6, щоб позбутися дробів:
 – 7 = 1 –
– 7 = 1 – 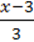 | ∙6,
| ∙6,
 ∙ 6 – 7 ∙ 6 = 1 ∙ 6 –
∙ 6 – 7 ∙ 6 = 1 ∙ 6 – 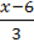 ∙ 6,
∙ 6,
Х – 42 = 6 – 2(х – 3).
Розкриємо дужки в правій частині рівняння: х – 42 = 6 – 2х + 6.
Доданок -2х перенесемо з протилежним знаком у ліву частину рівняння, а доданок -42 – у праву його частину:
Х + 2х = 6 + 6 + 42.
Зведемо подібні доданки:
3х = 54.
Поділивши обидві частини рівняння на 3, дістанемо: х = 18.
Отже, число 18 є коренем рівняння  – 7 = 1 –
– 7 = 1 – 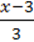 .
.
Рівняння класифікують за різними основами. Однією з таких основ є кількість змінних у рівнянні. Наприклад, рівняння 4х + 7 = 15 є рівнянням з однією змінною, рівняння 2х(3 – 5,1 у)=0 – із двома змінними, а рівняння x2+ y2 + z2 = 1 – із трьома змінними.
Рівняння також можна поділити на види за степенем многочлена, який “породжує” рівняння. Наприклад, рівняння 4х + 7 – 15 = 0 “породжується” многочленом 4х + 7 – 15. Цей многочлен – першого степеня, тому дане рівняння є рівнянням першого степеня. Міркуючи аналогічно, дістанемо, що рівняння 2х(3 – 5,1 y) = 0 i x2 + y2 + z2 = 1 є рівняннями другого степеня. Такі рівняння, а також рівняння вищих степенів ви вивчатимете в наступних класах.
1. Перші скорочені позначення для невідомих величин зустрічаються ще у Діофанта (III ст.). Його трактат “Арифметика” є збіркою задач на складання рівнянь, а їх розв’язання подано за певною системою.
У X ст. “Арифметика” була перекладена арабською мовою, після чого ісламські математики (Абу Каміл та ін.) продовжили деякі з досліджень Діофанта. У Європі інтерес до “Арифметики” з’явився після того, як Рафаель Бомбеллі знайшов цей твір у Ватиканській бібліотеці та опублікував 143 задачі з нього у своїй “Алгебрі” (1572 p.). У 1621 р. вийшов класичний, детально прокоментований латинський переклад “Арифметики” Діофанта, виконаний Ваше де Мезіріаком. Методи Діофанта мали великий вплив на наукову діяльність багатьох видатних математиків та розвиток математики як науки.

2. Конфорович Андрій Григорович (1923-1997) – фахівець у галузі історії математики і популяризації математичних знань в Україні. У його доробку – понад 200 друкованих праць. Вони присвячені математичній підготовці учнів, олімпіадам з математики, аналізу науково-популярної літератури з математики і кібернетики, застосуванням математики, питанням історії математики, математичним іграм і головоломкам. Основні з них: “Дорогами Унікурсалії”, “Визначні математичні задачі”, “Колумби математики”, “Математична мозаїка”, “Математичні софізми і парадокси”, “Математика служить людині”, “Добрий день, Архімеде!” та інші. Майже 20 років А. Г Конфорович був заступником відповідального редактора й активним дописувачем збірника науково-популярних статей “У світі математики”. На його сторінках він опублікував багато цікавих і актуальних статей, значна частина яких стосувалася життєвого і творчого шляху визначних математиків. Це статті: “Нільс Генрік Абель”, “Леонард Ейлер”, “Готфрід Вільгельм Лейбніц”, “Ісаак Ньютон” та ін.

ПРИГАДАЙТЕ ГОЛОВНЕ
1. Що таке рівняння?
2. Що називають коренем рівняння?
3. Що означає “розв’язати рівняння”?
4. Які рівняння називають рівносильними?
5. Сформулюйте властивості рівносильності рівнянь.
РОЗВ’ЯЖІТЬ ЗАДАЧІ
988. Яке з чисел -5, -1, 0,2, чи 4 є коренем рівняння:
1) 5х + 25 = 0; 2) 6у – 8 = 8; 3) 0,4x – 1,6 = 0; 4) 4у – 12 = 4?
989. Чи правильно, що дане рівняння: а) має рівно один корінь; 6) має більше ніж один корінь; в) не має коренів; в) має безліч коренів:
1) – 2x + 8 = 0; 4)6 + 2у =6 – у + 3у;
2) 0у + 25 = 0; 5)(х – 5)(х + 2) = 0;
3) 6x – 11 =-11; 6) у(у – 8)(4 – у) = 0?
990. Назвіть число, яке задовольняє рівняння:
1) 2х + 12 = 0; 2)3у – 1 = 8; 3)-5х – 10 = 10; 4)4у – 4 = 0.
991. Дано рівняння 4х – 9 = 0. Чи отримаємо рівносильне йому рівняння, якщо:
1) до лівої частини даного рівняння додамо число 9;
2) до правої частини даного рівняння додамо число -9;
3) до обох частин даного рівняння додамо число -9;
4) до обох частин даного рівняння додамо число 9?
Відповідь поясніть.
992. Дано рівняння -5х + 10 = 0. Чи отримаємо рівносильне йому рівняння, якщо:
1) доданок 10 перенести у праву частину рівняння;
2) доданок 10 перенести з протилежним знаком у праву частину рівняння;
3) обидві частини рівняння поділити на 5;
4) змінити знаки всіх доданків на протилежні?
Відповідь поясніть.
993. Якщо розв’язувати рівняння 2х + 24 = 0, то чи буде правильним такий крок:
1) 2х = 24; 2) 2х = -24; 3)24 = -2х; 4) х + 12 = 0?
Відповідь поясніть.
994. Яку властивість рівносильності треба використати, щоб від рівняння 0,5х – 2 = 0 перейти до рівняння:
1)0,5х = 2;
2) х – 4 = 0;
3) 5х – 20 = 0;
4)-0,5х + 2 = 0?
Відповідь поясніть.
995. Чи рівносильне рівнянню 2х + 8 = 0 рівняння:
1)2х + 8 – 8 = -8;
2)2х = -8;
3)х + 4 = 0;
4)4х + 16 = 0?
Відповідь поясніть.
996. Чи є рівносильним рівнянню 5у – 20 = 0 рівняння:
1)5у – 20 + 20 = 20; 2)5у = 20; 3)-5у + 20 = 0; 4)у – 4 = 0?
Відповідь поясніть.
997. Наведіть приклад чотирьох рівносильних рівнянь.
998. Складіть три рівносильні рівняння.
999. Чи є рівносильними рівняння:
1) х = – х і 5х = 6х;
2) у – 3у = 3 і 3у – у = 3;
3) 2(х + 1) = -2(5 + х) і 2х = -4;
4) 5(у – 2) – 5 = 0 і 4х = -12?
Відповідь обгрунтуйте.
1000. Чи є рівносильними рівняння:
1) 2х = 5 – 4х і 6х = 5; 2) у -12 = – у і 3у = 18?
Відповідь обгрунтуйте.
1001. Розв’яжіть рівняння:
1) 5х – 4 = 6; 7) 6z + 3 = 66 + 3z;
2) 5 – 2у = 11; 8) 5х – 22 = 5 – 4х;
3) 16 = 12 – 4х; 9)-12 – 7у = -4 + у;
4) -5 = 5у + 15; 10) 2у + 3у = 28 – 2у;
5) 2х = 4х + 12; 11) 18 – 12х + 3х = 6 – 5х;
6) -7у = 18 – 5у; 12) 5у – 10 – 9у = 12у – 42.
1002. Розв’яжіть рівняння:
1) 12 – 4х = 40; 4) 26 + 2х = 7х-9;
2) 7у – 27 = – 2у; 5) 35 + 17у – 5 = 2у;
3) 15 – 3у = 14 – 2у; 6) 12z = 5z – 18 – 2z.
1003. Складіть рівняння з однією змінною, коренем якого є число:
1)-2; 2)1 .
.
1004. Складіть рівняння з однією змінною, коренем якого є число:
1)5; 2)0.
1005. Знайдіть корінь рівняння:
1) (4х + 1) – (2х – 8) = 15;
2) 4 + 2(х – 5) = 4х;
3) 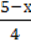 = х;
= х;
4)  +
+  = 12;
= 12;
5) 5y – 3(6y – 4) = 9;
6) 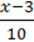 =
= 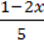 + 3.
+ 3.
1006. Знайдіть корінь рівняння:
1) 2x + 4(8 – х) = 2;
2) 16 – 8(y + 1) = y – 10;
3) 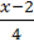 =
= 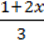 ;
;
4)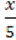 –
– 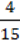 =
= 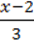 .
.
1007. Розв’яжіть рівняння:
1) 2(х – 4) – 2(5 – 6х) = 18;
2) 9(у + 2) = 8(1 – у) + 24;
3) 0,4х – 2,6 = 5(0,2 – х) – 0,3(х + 4);
4) 0,5(2 – х) + 2(4х – 0,2) + 5,9 = -5,5х;
5) (1,2 – 4у) ∙ 2 = 5у – 0,4(5 – 15у) – 1,3;
6) 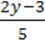 –
– 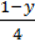 =
= 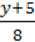 +
+ 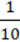 ;
;
7) 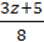 +
+  =
= 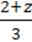 + 3;
+ 3;
8) 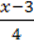 +
+ 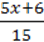 =
= 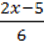 –
– 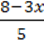 +
+ 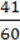 .
.
1008. Розв’яжіть рівняння:
1) 3(9 + х) – 6(х – 3) = 0;
2) 7у – 0,3(5 – 2у) = 0,4у + 4,5;
3)  +
+  =
=  –
–  ;
;
4) 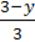 +
+ 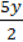 =1 –
=1 – 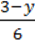 .
.
1009. Доведіть, що:
1) коренем рівняння х2 – 2х – 8 = (х – 4)(х + 4) – 2(х – 8) є будь – яке число;
2) рівняння 4(у + 1 )(у -1 )(у – 8) = 0 має три корені;
3) рівняння (х + 5)(х + 4) = х(х + 9) + 4 не має коренів.
1010. Доведіть, що:
1) рівняння (х + 6)(х – 6) – (5 + х)2 = 9 має один корінь;
2) рівняння 2у(у – 5) = (у + 4)2 + у2 – 10y не має коренів.
1011. Доведіть, що рівняння 0,7(х – 3) – (0,5 – 2х) = 0,9 (3х – 1) + 0,1 рівносильне рівнянню:
1) х2 = -1; 2) | х | =-5; 3) – 16х4 = 81.
1012. Розв’яжіть рівняння, якщо a ≠ 0, b ≠ 0:
1) (х + а)2 – 2 = -2х – (а2 – х);
2) x + 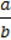 +
+  = 2;
= 2;
3)  –
– 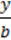 =
= 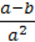 ;
;
4) 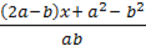 =
= 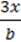 +
+ 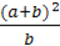 .
.
ЗАСТОСУЙТЕ НА ПРАКТИЦІ
1013. Про видатного математика давнини Діофанта відомо дуже мало, навіть невідомі роки його життя. На гробниці Діофанта напис складено у формі задачі. Розв’яжіть її та встановіть, скільки років прожив Діофант.
Подорожній! Поховано тут Діофанта.
І числа розкажуть тобі,
Який дивний шлях він життєвий пройшов.
Шосту частину його становило дитинство.
Минула частина дванадцята –
І пухом покрилось його підборіддя.
Сьому – в бездітному шлюбі прожив Діофант.
Минуло п’ять літ. Ощасливлений був він
Народженням первенця – сина,
Якому судилась лише половина життя його батька.
У глибокій журбі старець закінчив шлях на землі,
Ще проживши років чотири з часу,
Коли сина не стало.
Скажи, віку якого досягши, славетний помер Діофант.
1014. Складіть і розв’яжіть задачу про свій вік та значні події у вашому житті.
ЗАДАЧІ НА ПОВТОРЕННЯ
1015. Обчисліть:
1)2 ∙ 54 + 63 : 12 + 32;
2) (4 ∙ 52 – 43) : (22 + 2).
1016. Квадрат і прямокутник мають однаковий периметр. Довжина прямокутника на 2 см більша за ширину. Знайдіть сторони прямокутника, якщо сторона квадрата дорівнює 4 см. На скільки площа прямокутника менша від площі квадрата?