Розв’язування ірраціональних рівнянь, систем з ірраціональними рівняннями
УРОК 38
Тема. Розв’язування ірраціональних рівнянь, систем з ірраціональними рівняннями
Мета уроку. Формування умінь розв’язувати ірраціональні рівняння, системи з ірраціональними рівняннями.
І. Перевірка домашнього завдання
1. Відповіді на запитання учнів, що виникли в процесі виконання домашніх завдань.
2. Фронтальна бесіда за питаннями № 49-53 із “Запитання і завдання для повторення” до розділу III.
3. Усне розв’язування рівнянь (таблиця 16).
1 | 2 | 3 | 4 | 5 | |
1 |
|
|
| 3 + | |
2 |
|
|
|
| |
3 |
|
|
|
|
|
4 |
|
|
|
|
|
5 |
|
|
|
|
|
II. Формування умінь розв’язувати ірраціональні рівняння
Колективне розв’язування вправ
1. Розв’яжіть рівняння х2 + 3х – 18 + 4 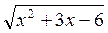 = 0 .
= 0 .
Розв’язання
Нехай 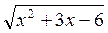 = t, t > 0, тоді х2 + 3х – 18 = t2 – 12 і дане рівняння стане таким: t2 – 12 + 4t = 0, звідси t1 = – 6, t2 = 2.
= t, t > 0, тоді х2 + 3х – 18 = t2 – 12 і дане рівняння стане таким: t2 – 12 + 4t = 0, звідси t1 = – 6, t2 = 2.
1) 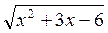 = – 6 – розв’язків немає.
= – 6 – розв’язків немає.
2) 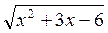 = 2, х2 + 3х – 6 = 4, х2 + 3x – 10 = 0, звідси х = – 5 або х = 2. Перевірка показує, що – 5 і 2 – корені.
= 2, х2 + 3х – 6 = 4, х2 + 3x – 10 = 0, звідси х = – 5 або х = 2. Перевірка показує, що – 5 і 2 – корені.
Відповідь: – 5; 2.
2. Розв’яжіть рівняння (вправа 77 (г)): 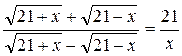 .
.
Домножимо чисельник і знаменник дробу лівої частини рівняння на 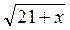 +
+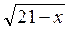 .
.
Тоді 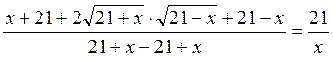 ,
,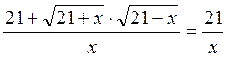 ,
,
21+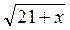 –
–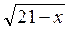 = 21,
= 21, 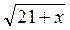 –
–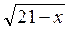 = 0.
= 0.
Звідси 21 – х = 0 або 21 + х = 0.
1) 21 – х = 0, х = 21; 2) 21 + x = 0, x = – 21.
Відповідь: 21; -21.
3. Розв’яжіть рівняння 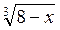 +
+ 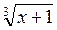 = 3.
= 3.
Розв’язання
Піднесемо до куба обидві частини рівняння і одержимо:
8 – x + 3(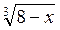 )2-
)2-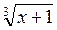 + 3
+ 3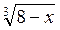 (
(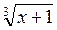 )2 + x + l = 27,
)2 + x + l = 27,
3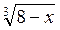
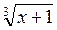 (
(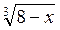 +
+ 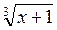 ) = 18.
) = 18.
За умовою 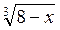 +
+ 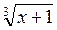 = 3, тому
= 3, тому
3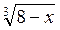
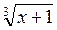 – 3 = 18 ,
– 3 = 18 ,
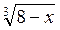
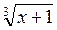 = 2,
= 2,
Х2 – 7х= 0.
Звідси х = 0, х = 7.
Перевіркою впевняємося, що обидві корені є коренями даного рівняння. Відповідь: 0; 7.
III. Формування умінь розв’язувати системи з ірраціональними рівняннями
1. Розв’яжіть систему рівнянь 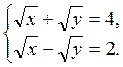
Розв’язання
Додавши почленно ліві і праві частини рівнянь, одержуємо 2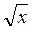 = 6, звідси
= 6, звідси 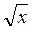 = 3 , х = 9.
= 3 , х = 9.
Віднявши почленно ліві і праві частини рівнянь, одержуємо 2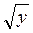 = 2, звідси
= 2, звідси 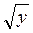 = 1, у = 1.
= 1, у = 1.
Відповідь: (9; 1).
2. Розв’яжіть систему рівнянь 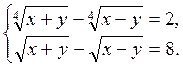
Розв’язання
Введемо нові змінні: 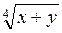 = а,
= а, 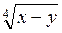 = b. Дана система приймає вигляд:
= b. Дана система приймає вигляд:
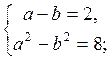
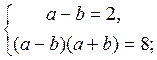
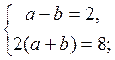
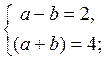
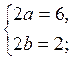
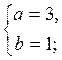
Повертаючись до даних змінних, одержимо:
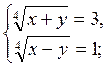
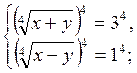
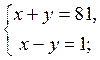
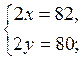
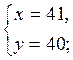
Перевірка: 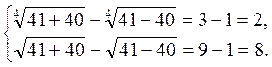
Відповідь: (41; 40).
III. Підведення підсумків уроку
IV. Домашнє завдання
Розділ ПІ § 2 (2). Запитання і завдання для повторення розділу III № 54. Вправи № 71 (3), 67 (1), 79 (1).
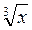 = – 2
= – 2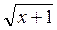 = – 2
= – 2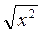 = 9
= 9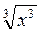 = х
= х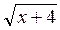 = 5
= 5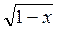 = 2
= 2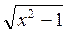 =
=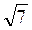
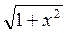 =
=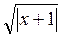 = 0
= 0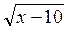 =10 – х
=10 – х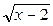 +
+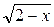 =0
=0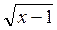 +
+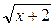 +1=0
+1=0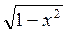 = 2
= 2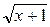 +
+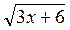 + 2 = 1
+ 2 = 1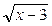 =0
=0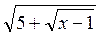 =2
=2