Розв’язування однорідних тригонометричних рівнянь
УРОК 25
Тема. Розв’язування однорідних тригонометричних рівнянь
Мета уроку: формування умінь учнів розв’язувати однорідні тригонометричні рівняння.
І. Перевірка домашнього завдання
1. Обговорення розв’язування вправи № 2 (6; 9; 11) за готовими розв’язаннями.
2. Розв’язування аналогічних вправ.
А) 1 + cos x + cos 2x = 0;
Б) cos4 x – sin4 x = 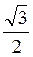 ;
;
В) cos 4х + sin 2x = 0;
Г) cos x (tg x – 1) = 0.
Відповіді: а)  + ?n, ±
+ ?n, ± 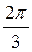 + 2 ?n, n
+ 2 ?n, n Z; б) ±
Z; б) ± 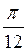
 Z;
Z;В) (-1)n+1 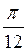 +
+ 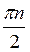 ;
;  + ?n, n
+ ?n, n Z; г)
Z; г)  + ?n, n
+ ?n, n Z.
Z.
II. Сприймання і усвідомлення нового матеріалу
1) Розглянемо рівняння виду asin x + bcos x = 0 (однорідне рівняння 1-го степеня), де а і b не дорівнюють нулю. Значення x, при яких cos x дорівнює нулю, не задовольняє даному рівнянню, бо тоді і sin x теж дорівнював би нулю, а cos x і sin x не можуть одночасно дорівнювати нулю. Тому можна розділити обидві частини рівняння почленно на cos x. Маємо:
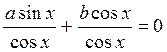 ; atg x + b = 0; tg x = –
; atg x + b = 0; tg x = –
X = – arctg 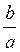 + ?n, n
+ ?n, n Z.
Z.
Виконання вправ
Розв’яжіть рівняння.
1. а)  Sinx + cosx = 0;
Sinx + cosx = 0;
Б) 16sin x = 5cos x;
В) 2cos 2x + 3sin 2x = 0;
Г) sin2 x + sin x cos x = 0.
Відповідь: а) – +?n, n
+?n, n Z; б) arctg
Z; б) arctg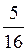 + ?n, n
+ ?n, n Z; в) –
Z; в) – Arctg
Arctg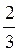 +
+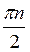 , n
, n Z; г) ?n, –
Z; г) ?n, – + ?n, n
+ ?n, n Z.
Z.
2. Рівняння виду a sin2x + b sinx cosx + c cos2x = 0 називається однорідним рівнянням 2-го степеня. Якщо числа а, b, с не дорівнюють нулю, то розділимо дане рівняння на cos2 x (або на sin2x). (У даному рівнянні cos2x? 0, бо в супротивному випадку sin2 x теж дорівнював би нулю, а cos x і sin x не можуть одночасно дорівнювати нулю). Тоді
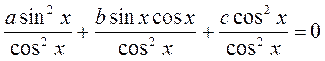 ;
;
Atg2x + btgx + c = 0.
Розв’язавши отримане, рівняння одержимо корені даного рівняння.
Виконання вправ
1. Розв’яжіть рівняння:
А) sin2 x = 3cos2 x;
Б) sin2 x – 3 sin x cos x + 2 cos2 x = 0;
В) 3sin2 x – 4sin x cos x +cos2 x = 0;
Г) sin2 x – 5sin x cos x + 6cos2 x = 0.
Відповідь: а) ±  + ?n, n
+ ?n, n Z; б) arctg 2 + ?n,
Z; б) arctg 2 + ?n,  + ?n, n
+ ?n, n Z; в)
Z; в)  + ?n, arctg
+ ?n, arctg 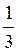 + ?n, n
+ ?n, n Z; г) arctg 2 + ?n, arctg 3 + ?n, n
Z; г) arctg 2 + ?n, arctg 3 + ?n, n Z.
Z.
3. Рівняння виду аn sinn x + an-1 sinn-1x cos x +… + a1 sinx cosn-1x + a0 cosn x = 0
Називається однорідним рівнянням n-го степеня відносно синуса і косинуса.
Якщо жоден із коефіцієнтів an, а n-1, … , а1, a0 не дорівнює нулю, то, розділивши обидві частини рівняння почленно на cosnx, одержимо рівняння n-го степеня відносно tgx. Якщо хоча б один із коефіцієнтів an, а n-1, … , а1, a0 дорівнює нулю, то перш ніж виконувати ділення на cosnx, слід довести, що cosnx? 0, тобто, cos x? 0.
Розглянемо приклад:
Розв’яжіть рівняння cos2 x – 2 cos x sin x = 0.
Ділити обидві частини на cos2 x не можна, бо cos2 x = 0 є розв’язком даного рівняння. Це рівняння можна розв’язати:
І спосіб (винесення множника)
Cos2 x – 2 cos x sin x = 0
Cos x (cos x – 2 sin x) = 0
Звідси cosx = 0 або cosx – 2sinx = 0.
1) cos x = 0; x =  + ?n, n
+ ?n, n Z.
Z.
2) cosx – 2sinx = 0; 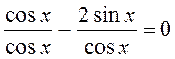 ; 1 – 2tgx = 0; tgx =
; 1 – 2tgx = 0; tgx =  ; x = arctg
; x = arctg  + ?n, n
+ ?n, n Z.
Z.
Відповідь:  + ?n, n
+ ?n, n Z; arctg
Z; arctg  + ?n, n
+ ?n, n Z.
Z.
II спосіб. Розділимо обидві частини на sin2 x, оскільки sin x? 0 в даному рівнянні, бо в супротивному випадку і cos x = 0, що неможливо.
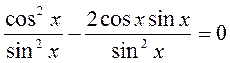 ,
,
Ctg2 x – 2ctg x = 0;
Ctgх(ctg x – 2) = 0.
Звідси ctg x = 0, або ctg x = 2.
1) ctg x = 0; x =  + ?n, n
+ ?n, n Z.
Z.
2) ctg x = 2; x = arcctg 2 + ?n, n Z.
Z.
Відповідь:  + ?n, arcctg 2 + ?n, n
+ ?n, arcctg 2 + ?n, n Z.
Z.
Виконання вправ
1. Розв’яжіть рівняння:
А) sin 2х – cos2 x = 0;
Б) 2 sin2 x =  Sin 2х;
Sin 2х;
В) 3 sin 2х + cos 2х = cos2 x;
Г) 1 – cos x = 2 sin 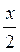 cos
cos 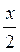 .
.
Відповідь: a)  + ?n, arctg
+ ?n, arctg  + ?n, n
+ ?n, n Z; б) ?n,
Z; б) ?n,  + ?n, n
+ ?n, n Z; в) ?n, arctg 6 + ?n, n
Z; в) ?n, arctg 6 + ?n, n Z; г) 2?n,
Z; г) 2?n,  + 2?n, n
+ 2?n, n Z.
Z.
2. Розв’яжіть рівняння:
А) 4sin2 x – sin2x = 3;
Б) sin 2х + 4cos2 x = 1;
В) 5 sin2 x + 3 sin x cos x – 4 = 0;
Г) 2 sin x + cos x = 2.
Відповідь: а) arctg 3 + ?n, –  + ?n, n
+ ?n, n Z; б) arctg3 + ?n, –
Z; б) arctg3 + ?n, –  + ?n, n
+ ?n, n Z; в) – arctg 4 + ?n,
Z; в) – arctg 4 + ?n,  + ?n, n
+ ?n, n Z; г)
Z; г)  + 2?n, 2arctg
+ 2?n, 2arctg 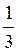 + 2 ?n, n
+ 2 ?n, n Z.
Z.
III. Підведення підсумків уроку
IV. Домашнє завдання
Розділ II § 3 (3). Запитання і завдання для повторення до розділу II № 17, 18. Вправа № 2 (8; 17; 22; 28; 36).