Розв’язування тригонометричних рівнянь способом розкладання на множники
УРОК 24
Тема. Розв’язування тригонометричних рівнянь способом розкладання на множники
Мета уроку: фрмування умінь учнів розв’язувати тригонометричні рівняння способом розкладання на множники.
І. Перевірка домашнього завдання
Перший учень пояснює розв’язування вправи № 2 (23), другий учень – вправи № 2 (30), третій – вправи № 2 (37).
II. Сприймання і усвідомлення нового матеріалу
Багато тригонометричних рівнянь, права частина яких дорівнює 0, розв’язуються розкладанням їхньої лівої частини на множники.
Розглянемо
Приклад 1. Розв’яжіть рівняння 1 + cos x – 2 cos 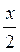 = 0.
= 0.
Врахувавши, що 1 + cos х = 2 cos 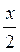 , матимемо:
, матимемо:
2cos2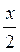 – 2cos
– 2cos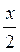 = 0, 2cos
= 0, 2cos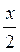
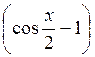 = 0.
= 0.
Добуток дорівнює нулю, якщо хоча б один із множників дорівнює нулю. Тому:
1) cos 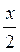 = 0;
= 0; 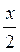 =
=  +?n, n
+?n, n  Z; х = ? + 2 ?n, n
Z; х = ? + 2 ?n, n Z;
Z;
2) cos 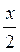 = 1;
= 1; 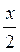 = 2?n, п
= 2?n, п  Z; х = 4 ?n, n
Z; х = 4 ?n, n Z.
Z.
Відповідь:
 Z.
Z.Приклад 2. Розв’яжіть рівняння sin 2х – sin х = 0.
Sin 2х – sin х = 0; 2 sin 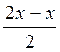 cos
cos 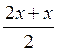 = 0; 2 sin
= 0; 2 sin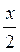 Cos
Cos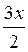 = 0.
= 0.
1) sin 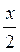 = 0;
= 0; 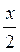 = ?n, х = 2 ?n, n
= ?n, х = 2 ?n, n Z.
Z.
2) cos 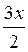 = 0,
= 0, 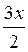 =
=  +?n, х =
+?n, х =  +
+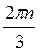 , n
, n Z.
Z.
Відповідь: 2?n і  +
+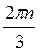 , n
, n Z.
Z.
III. Формування умінь і навичок учнів розв’язувати тригонометричні рівняння способом розкладання на множники
Виконання вправ______________________________
Розв’яжіть рівняння.
1. a)  cos х = sin2 х cos х;
cos х = sin2 х cos х;
6) 2sin 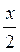 = 3sin2
= 3sin2 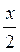 ;
;
В) sin 2x =  Sin x;
Sin x;
Г)  Cos2 4х + cos 4x = 0.
Cos2 4х + cos 4x = 0.
Відповідь: а)  +?n, n
+?n, n Z; б) 2?n, (-1)n2arcsin
Z; б) 2?n, (-1)n2arcsin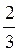 + 2 ?n, n
+ 2 ?n, n Z; в) ?n, ±
Z; в) ?n, ±  + 2 ?n, n
+ 2 ?n, n Z; г)
Z; г) 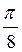 +
+ 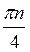 , ±
, ± 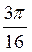 +
+ 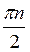 , n
, n Z.
Z.
2. a) cos 7x + cos х = 0;
Б) sin 7x = sin х;
В) cos 3х + sin 5x = 0;
Г) sin 7x + sin 3х = 3cos 2х.
Відповіді: а) 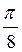 +
+ 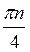 ,
,  +
+ 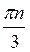 , n
, n Z; б)
Z; б) 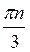 ,
, 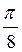 +
+ 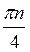 , n
, n Z; в)
Z; в) 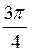 +?n,
+?n, 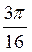 +
+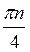 , n
, n Z; г)
Z; г)  +
+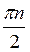 , n
, n Z.
Z.
IV. Підведення підсумків уроку
V. Домашнє завдання
Розділ II § 3 (2). Запитання і завдання для повторення розділу II № 16. Вправа № 2 (5; 6; 9; 11).
Related posts:
- Розкладання багаточленів на множники способом групування Урок № 40 Тема. Розкладання багаточленів на множники способом групування Мета: вдосконалити вміння та відпрацювати навички розкладання багаточленів на множники способом групування та використання цього перетворення многочленів для розв’язування різноманітних завдань. Тип уроку: застосування знань, умінь та навичок. Хід уроку І. Перевірка домашнього завдання @ Оскільки № 1 та 2 домашнього завдання були вправами на […]...
- Розкладання многочленів на множники способом винесення спільного множника за дужки Розділ 1. ЦІЛІ ВИРАЗИ & 10. Розкладання многочленів на множники способом Винесення спільного множника за дужки У 6 класі ми розкладали складені числа на прості множники, тобто подавали натуральні числа у вигляді добутку. Наприклад, 12 = 22 ∙ 3; 105 = 3 ∙5 ∙ 7 тощо. Подати у вигляді добутку можна і деякі многочлени. Це […]...
- РОЗКЛАДАННЯ МНОГОЧЛЕНІВ НА МНОЖНИКИ СПОСОБОМ ГРУПУВАННЯ Цілі: – навчальна: удосконалити вміння розкладати многочлени на множники способом групування; сформувати вміння застосовувати цей спосіб до розв’язання рівнянь та доведення тверджень; – розвивальна: формувати вміння орієнтуватися у видозміненій ситуації; розвивати творчі здібності, кмітливість учнів; – виховна: виховувати інтерес до вивчення математики, наполегливість у досягненні мети, спостережливість; Тип уроку : удосконалення та застосування знань і […]...
- РОЗКЛАДАННЯ МНОГОЧЛЕНІВ НА МНОЖНИКИ СПОСОБОМ ВИНЕСЕННЯ СПІЛЬНОГО МНОЖНИКА ЗА ДУЖКИ Цілі: – навчальна: удосконалити вміння учнів виконувати розкладання многочленів на множники способом винесення спільного множника за дужки; – розвивальна: формувати вміння міркувати за аналогією; розвивати увагу, логічне мислення, пам’ять; сприяти удосконаленню обчислювальних навичок; – виховна: виховувати впевненість у власних силах, спостережливість; формувати вміння самоорганізовуватися; Тип уроку : удосконалення вмінь і навичок. Обладнання та наочність: Хід […]...
- Розв’язування тригонометричних рівнянь способом зведення до однієї тригонометричної функції УРОК 23 Тема. Розв’язування тригонометричних рівнянь способом зведення до однієї тригонометричної функції Мета уроку: формування умінь учнів розв’язувати тригонометричні рівняння способом зведення до однієї тригонометричної функції (алгебраїчний спосіб). І. Перевірка домашнього завдання 1. Відповіді на питання, що виникли у учнів при виконанні домашніх завдань. 2. Самостійна робота. Розв’яжіть рівняння: A) cosx = . (3 бали) […]...
- Розкладання на множники різниці квадратів двох виразів Розділ 1. ЦІЛІ ВИРАЗИ & 16. Розкладання на множники різниці квадратів двох виразів У тотожності (а – b)(а + b) = а2 – b2 поміняємо місцями ліву і праву частини. Матимемо: Цю тотожність називають формулою різниці квадратів двох виразів. Читають її так. Формулу різниці квадратів двох виразів застосовують для розкладання на множники двочлена а2 – […]...
- ЗАСТОСУВАННЯ РІЗНИХ СПОСОБІВ РОЗКЛАДАННЯ МНОГОЧЛЕНІВ НА МНОЖНИКИ Цілі: – навчальна: удосконалити вміння розкладати многочлени на множники, використовуючи різні способи; ознайомити учнів з основними видами задач, для розв’язування яких доцільно розкладати многочлени на множники; сформувати вміння розв’язувати задачі, які передбачають розкладання многочленів на множники; – розвивальна: формувати вміння вибирати і використовувати необхідну інформацію для розв’язування задач; сприяти вдосконаленню обчислювальних навичок; – виховна: виховувати […]...
- Розв’язування систем тригонометричних рівнянь УРОК 27 Тема. Розв’язування систем тригонометричних рівнянь Мета уроку: познайомити учнів з окремими прийомами розв’язування систем тригонометричних рівнянь. І. Перевірка домашнього завдання 1. Чотири учні відтворюють розв’язування домашніх завдань: вправа № 2 (10; 18; 26; 38). 2. Усне розв’язування тригонометричних рівнянь, використовуючи таблицю “Тригонометричні рівняння”. 1 2 3 4 1 Sin x = 0 Cos […]...
- Застосування кількох способів для розкладання многочленів на множники Математика – Алгебра Многочлен Застосування кількох способів для розкладання многочленів на множники Щоб розкласти многочлен на множники, бажано діяти в такій послідовності. 1. З’ясувати, чи можна винести за дужки спільний множник. Зробити це, якщо можна. 2. Розглянути, чи можна вираз, який залишився в дужках (або даний), розкласти на множники за формулами скороченого множення. 3. Спробувати […]...
- Застосування різних способів розкладання багаточленів на множники Урок № 54 Тема. Застосування різних способів розкладання багаточленів на множники Мета: відпрацювати навички застосування спеціальних прийомів та класичних методів розкладання багаточленів на множники; продовжувати знайомство учнів зі сферою застосування розкладання багаточленів на множники; узагальнити та систематизувати набуті з теми знання та уміння і навички. Тип уроку: комбінований. Хід уроку I. Організаційний момент Перевіряємо готовність […]...
- Розкладання многочленів на множники способом групування Розділ 1. ЦІЛІ ВИРАЗИ & 13. Квадрат суми і квадрат різниці Піднесемо до квадрата двочлен а + b: (а + b)2 = (а + b)(а + b) = а2 + аb + bа + b2 = а2 + 2ab + b2. Отже, Одержану тотожність називають формулою квадрата суми. Ця тотожність дає змогу підносити до квадрата […]...
- Розкладання багаточленів на множники винесенням спільного множника за дужки Урок № 38 Тема. Розкладання багаточленів на множники винесенням спільного множника за дужки Мета: відпрацювати навички розкладання багаточленів на множники винесенням спільного множника за дужки; удосконалити вміння застосовувати винесення спільного множника за дужки. Тип уроку: застосування знань, умінь та навичок. Хід уроку I. Перевірка домашнього завдання Математичний диктант Варіант 1 [2] 1. Який степінь множника […]...
- ЗАСТОСУВАННЯ ФОРМУЛ СКОРОЧЕНОГО МНОЖЕННЯ ДО РОЗКЛАДАННЯ МНОГОЧЛЕНІВ НА МНОЖНИКИ Цілі: – навчальна: сформувати вміння розкладати многочлени на множники, використовуючи формули скороченого множення; – розвивальна: формувати вміння орієнтуватися у видозміненій ситуації; розвивати творчі здібності, кмітливість учнів; – виховна: виховувати інтерес до вивчення математики, наполегливість у досягненні мети; Тип уроку : засвоєння нових знань, умінь, навичок. Обладнання та наочність: Хід уроку І. ОРГАНІЗАЦІЙНИЙ ЕТАП ______________________________________________________ ______________________________________________________ […]...
- Квадратний тричлен та його корені. Розкладання квадратного тричлена на лінійні множники Урок № 57 Тема. Квадратний тричлен та його корені. Розкладання квадратного тричлена на лінійні множники Мета: домогтися закріплення учнями означення квадратного тричлена та його коренів, а також формули розкладання квадратного тричлена на лінійні множники; вдосконалити вміння відтворювати вивчені означення і формули та використовувати їх для розв’язування завдань на знаходження коренів квадратного тричлена та розкладання квадратного […]...
- Розкладання числа на прості множники Математика – Алгебра Подільність натуральних чисел Розкладання числа на прості множники Розкласти число на прості множники означає записати його у вигляді добутку простих чисел. Наприклад, . Кожне складене число можна розкласти на прості множники єдиним способом (якщо не враховувати порядок множників). Розкладання зручно робити за такою схемою. Наприклад, візьмемо число 2100. Запишемо число 2100 і […]...
- ЗАСТОСУВАННЯ ФОРМУЛ СКОРОЧЕНОГО МНОЖЕННЯ ДЛЯ РОЗКЛАДАННЯ МНОГОЧЛЕНІВ НА МНОЖНИКИ Цілі: – навчальна: удосконалити вміння розкладати многочлени на множники, використовуючи формули скороченого множення; – розвивальна: формувати вміння міркувати за аналогією; розвивати увагу, логічне мислення, пам’ять; – виховна: виховувати старанність, уважність, скрупульозність, самостійність; Тип уроку : удосконалення вмінь і навичок. Обладнання та наочність: Хід уроку І. ОРГАНІЗАЦІЙНИЙ ЕТАП ______________________________________________________ ______________________________________________________ ______________________________________________________ ІІ. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ 1. […]...
- Розв’язування найпростіших тригонометричних рівнянь. Рівняння cos t = a УРОК 20 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння cos T = a Мета уроку: засвоєння учнями виведення і застосування формули для знаходження коренів рівняння cos t = a. Обладнання: Таблиця “Рівняння cos t = a”. І. Перевірка домашнього завдання Математичний диктант Обчисліть: 1) arcsin ; 2) arcos ; 3) arctg ; 4) arcsin; 5) arccos; […]...
- Розв’язування однорідних тригонометричних рівнянь УРОК 25 Тема. Розв’язування однорідних тригонометричних рівнянь Мета уроку: формування умінь учнів розв’язувати однорідні тригонометричні рівняння. І. Перевірка домашнього завдання 1. Обговорення розв’язування вправи № 2 (6; 9; 11) за готовими розв’язаннями. 2. Розв’язування аналогічних вправ. А) 1 + cos x + cos 2x = 0; Б) cos4 x – sin4 x = ; В) […]...
- Розв’язування найпростіших тригонометричних рівнянь. Рівняння tg t = a УРОК 22 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння tg T = a. Мета уроку: зсвоєння учнями виведення і застосування формули для знаходження коренів рівняння tg t = a (ctg t = а). Обладнання: Таблиця “Рівняння tg t = а і ctg t = a”. І. Перевірка домашнього завдання 1. Перевірити наявність домашніх завдань в зошитах […]...
- Розв’язування тригонометричних рівнянь, систем та нерівностей УРОК 31 Тема. Розв’язування тригонометричних рівнянь, систем та нерівностей Мета уроку. Систематизувати навички і уміння розв’язувати тригонометричні рівняння, нерівності, системи. І. Перевірка домашнього завдання 1. Три учні відтворюють розв’язування нерівностей із домашнього завдання. 2. Колективне розв’язування нерівностей: A) sin 2x sin x – cos 2x cos х . Sin 2x sin x – cos 2x […]...
- Степінь натурального числа. Розкладання натурального числа на прості множники Урок № 4 Тема. Степінь натурального числа. Розкладання натурального числа на прості множники Мета: повторити знання учнів про степінь натурального числа з натуральним показником, здобутих у 5 класі, і сформувати вміння використовувати алгоритм розкладання складених чисел на прості множники. Тип уроку: засвоєння нових знань. Хід уроку I. Перевірка домашнього завдання @ Оскільки програмою передбачений дуже […]...
- Розв’язування найпростіших тригонометричних рівнянь. Рівняння sin t = a УРОК 21 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння sin t = а Мета уроку: засвоєння учнями виведення і застосування формули для коренів рівняння sin t = а. Обладнання: Таблиця “Рівняння sin t = а”. І. Перевірка домашнього завдання 1. Відповіді на питання, що виникли при виконанні домашніх завдань. 2. Самостійна робота. Варіант 1 Розв’яжіть рівняння: […]...
- Використання формул скороченого множення для розкладання багаточленів на множники Урок № 49 Тема. Використання формул скороченого множення для розкладання багаточленів на множники Мета: виробити в учнів уміння розкладати різницю квадратів та суму й різницю кубів на множники із використанням відповідних формул скороченого множення. Тип уроку: застосування знань, умінь та навичок. Хід уроку I. Організаційний момент Учитель спонукає учнів до само – та взаємоперевірки готовності […]...
- Розв’язання систем лінійних рівнянь способом підстановки Рівень А Відповідь: (1; 3). Відповідь: (7; -4,5). Відповідь: (1; 3). Відповідь: (4; 1). Відповідь: (3; 1). Відповідь: (1;-2). Відповідь: розв’язків немає. Відповідь: (3; 2). Відповідь: (4; 0). Відповідь: (3; 5). Відповідь: (1,5; 2). Відповідь: (3; -1). Відповідь: (7; 1). Відповідь: (1; -1). Рівень Б Відповідь: (2; 1,5). Відповідь: (1; -2). Відповідь: (20; 0,5). Відповідь: […]...
- Використання формул скороченого множення для розкладання багаточленів на множники. Формули скороченого множення Урок № 50 Тема. Використання формул скороченого множення для розкладання багаточленів на множники. Формули скороченого множення Мета: відпрацювати навички класифікації виразів та застосування формул скороченого множення для розкладання багаточленів та цілих виразів на множники та розв’язування вправ, що передбачають виконання цих Дій; повторити способи дій у разі використання формул скороченого множення для перетворення цілих виразів […]...
- Розкладання чисел на прості множники Розділ 1 Подільність натуральних чисел §5. Розкладання чисел на прості множники Кожне складене число можна подати у вигляді добутку хоча б двох множників, відмінних від одиниці. Наприклад, 330 = 10 ∙ 33. Якщо серед таких множників є складені числа, то їх також можна подати у вигляді добутку двох множників. Наприклад, 330 = 10 ∙ 33 […]...
- Розкладання многочленів на множники Математика – Алгебра Многочлен Розкладання многочленів на множники Розкласти многочлен на множники означає подати його як добуток кількох многочленів. Винесення спільного множника за дужки Спосіб розкладання многочлена на множники на основі розподільної властивості множення називається винесенням спільного множника за дужки. Приклад . НСД . Це означає, що за дужки можна винести числовий множник 2. В […]...
- Розв’язання систем лінійних рівнянь способом додавання Рівень А Відповідь: (4; 3). Відповідь: (-2; -3). Відповідь: (0,5; 1). Відповідь: (-1;2). Відповідь: (-2; 4). Відповідь: (5; 1). Відповідь: (3; -1). Відповідь: (0; -2). Відповідь: (-1; 3). Відповідь: (-1; -1). Відповідь: (2; -2). Відповідь: (4; -3). Відповідь: (-0,5; 0,5). Відповідь: (1; -1). Відповідь: (1; -2). Відповідь: (1; -2). Відповідь: (5; 6). Відповідь: (5; 0,5). […]...
- Розкладання многочленів на множники за допомогою формул квадрата суми і квадрата різниці Розділ 1. ЦІЛІ ВИРАЗИ & 14. Розкладання многочленів на множники За допомогою формул квадрата суми і квадрата різниці Формули квадрата суми і квадрата різниці можна використовувати також для розкладання на множники виразів вигляду а2 + 2аb + b2 і а2 – 2ab +b2. Для цього перепишемо ці формули, помінявши місцями їх ліву і праву частини. […]...
- Деякі способи розв’язування тригонометричних рівнянь Математика – Алгебра Тригонометричні функції Деякі способи розв’язування тригонометричних рівнянь 1. Рівняння, що зводяться до квадратних . легко виразити через за допомогою основної тригонометричної тотожності : . Отже, ; . Нехай , . ; ; . 1) ; , k Є Z. 2) ; , k Є Z. Відповідь: , k Є Z; , k […]...