Головна ⇒ 📌Довідник з геометрії ⇒ Скалярний добуток векторів
Скалярний добуток векторів
Геометрія
Вектори
Скалярний добуток векторів
Скалярним добутком векторів 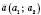 і
і 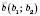 називається число
називається число 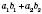 .
.
Позначення: 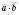 .
.
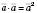 . Очевидно, що
. Очевидно, що 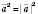 .
.
Розподільна властивість скалярного добутку: 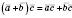 .
.
Кутом між ненульовими векторами 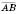 і
і 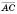 називається кут BAC. Кутом між будь-якими двома ненульовими
називається кут BAC. Кутом між будь-якими двома ненульовими
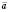 і
і 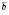 називається кут між векторами, що дорівнюють даним і мають спільний початок. Вважають, що кут між однаково напрямленими векторами дорівнює 0.
називається кут між векторами, що дорівнюють даним і мають спільний початок. Вважають, що кут між однаково напрямленими векторами дорівнює 0.Теорема 1. Скалярний добуток векторів дорівнює добутку їхніх абсолютних величин і косинуса кута між ними:
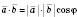 (див. рисунок).
(див. рисунок).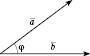
Звідси
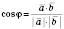 .
.Теорема 2. Два ненульові вектори перпендикулярні тоді й тільки тоді, коли їх скалярний добуток дорівнює 0.
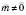 ;
; 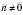 ;
; 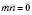
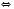
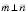 .
.Related posts:
- Кут між векторами. Скалярний добуток векторів Урок 59 Тема. Кут між векторами. Скалярний добуток векторів Мета уроку: формування понять кута між векторами, скалярного добутку векторів. Формування вмінь учнів застосовувати вивчений матеріал до розв’язування задач. Обладнання: схема “Вектори в просторі” Хід уроку 1. Фронтальна бесіда з класом за контрольними запитаннями № 18- 20 з використанням схеми “Вектори в просторі” (див. с. 233). […]...
- Скалярний добуток векторів УРОК № 49 Тема. Скалярний добуток векторів Мета уроку: формування поняття скалярного добутку векторів; формування вмінь застосовувати вивчені означення та властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині”[13]. Вимоги до рівня підготовки учнів: формулюють означення скалярного добутку, його властивості; застосовують вивчені означення та властивості до розв’язування […]...
- Векторний добуток векторів 1. Векторний добуток векторів є вектором, а скалярний – числом. Векторний та скалярний добуток мають однакові властивості (крім комутативності). 2. За означенням модуля векторного добутку А отже, оскільки то 3. 1) За означенням У нашому випадку Скористаємось основною тригонометричною тотожністю: Тоді 2) За означенням У нашому випадку Скористаємось основою тригонометричною тотожністю: Тоді Оскільки 3) Рівність […]...
- Розв’язування задач на застосування векторів Урок 60 Тема. Розв’язування задач на застосування векторів Мета уроку: формування вмінь учнів застосовувати вивчений матеріал до розв’язування задач. Обладнання: стінна таблиця “Вектори в просторі”. Хід уроку І. Перевірка домашнього завдання 1. Два учні відтворюють розв’язування задач № 55 (4), 56. 2. Фронтальне опитування. 1) Чому дорівнює скалярний добуток векторів, які задано координатами? 2) Як […]...
- Вектори в просторі – Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Вектори в просторі Усі основні означення векторів у просторі залишаються такими самими, як означення векторів на площині (див. розділ “Геометрія. 8 клас”). Координатами вектора , де , , називають числа, , . Вектори рівні тоді, й тільки тоді, коли вони мають відповідно рівні координати. Це дає підставу позначити […]...
- Скалярний добуток векторів. Кут між векторами 233. А) Якщо то α = 90°, α – кут між векторами. Б) то α – гострий; А) то α – тупий. 234. А) Б) В) Г) 235. А) Б) 236. А) Б) В) Г) 237. А) Б) В) 238. α – кут між векторами А) Б) В) Г) 239. А) Звідси Б) Звідси В) […]...
- Вектори в просторі (рівність векторів, колінеарність векторів, компланарність векторів). Додавання, віднімання векторів, множення вектора на число, властивості дій над векторами Урок 58 Тема. Вектори в просторі (рівність векторів, колінеарність векторів, компланарність векторів). Додавання, віднімання векторів, множення вектора на число, властивості дій над векторами Мета уроку: формування знань учнів про вектори в просторі, дії над векторами, заданими координатами, Формування вмінь застосовувати вивчений матеріал до розв’язування задач. Обладнання: схема “Вектори в просторі”. Хід уроку І. Перевірка домашнього […]...
- Вектори у просторі – ВЕКТОРИ Формули й таблиці МАТЕМАТИКА ВЕКТОРИ Вектори у просторі Вектор – спрямований відрізок А – початок вектора В – кінець вектора Модуль вектора – довжина відрізка, який зображує вектор: ||. Два вектори рівні, якщо вони однаково спрямовані і мають рівні модулі. Координати вектора з початком у точці А(x1,y1,z1) і кінцем у точці В(х2,у2,z2). Рівні вектори мають […]...
- Додавання векторів Геометрія Вектори Додавання векторів Сумою векторів і називається вектор . Додавання векторів має переставну та сполучну властивості: ; для будь-яких , , . Теорема. Які б не були точки A, B, C, справджується векторна рівність: . Правило трикутника додавання векторів Щоб знайти суму довільних векторів і , треба від кінця вектора (див. рисунок) відкласти вектор […]...
- Розв’язування задач координатно-векторним методом 1. 1) Введемо прямокутну систему координат із початком у точці В і спрямуємо вісь Оx вздовж ребра BA, Oz – вздовж ВВ1. Довжину ребра куба позначимо як а. Тоді координати точок: А(а; 0; 0;); С(0; а; 0); R(а; а; 0); C1(0; а; а). Знайдемо координати векторів і Знайдемо довжини векторів: Знайдемо кут між векторами: Кут […]...
- Віднімання векторів – Елементи векторної алгебри 3. Елементи векторної алгебри 3.3. Віднімання векторів Різницею двох векторів, спрямованих по одній прямій або паралельних один одному, є алгебраїчна різниця цих векторів. Щоб знайти різницю двох векторів, які мають різні напрями, треба розмістити обидва вектори так, щоб вони виходили з однієї точки. Потім сполучити кінці векторів вектором, спрямованим від від’ємника до зменшуваного. Цей вектор […]...
- Додавання векторів – Елементи векторної алгебри 3. Елементи векторної алгебри Векторні величини (вектори) – це величини, які характеризуються числовими значеннями і напрямом: Скалярні величини (скаляри) – це величини, які характеризуються лише числовим значенням. Вони можуть бути додатними та від’ємними й додаються алгебраїчно. 3.1. Додавання векторів Якщо вектори спрямовані вздовж однієї прямої або якщо вони паралельні, то результуючий вектор дорівнює алгебраїчній сумі […]...
- Додавання векторів за правилом паралелограма – Елементи векторної алгебри 3. Елементи векторної алгебри 3.2. Додавання векторів за правилом паралелограма Щоб додати два вектори за правилом паралелограма, треба розмістити їх так, не змінюючи їх напряму, щоб вони виходили з однієї точки, й добудувати на кінцях векторів паралельні прямі. Діагональ одержаного паралелограма, проведена з точки, в якій суміщені початки обох векторів, є їх сумою....
- Додавання векторів УРОК № 44 Тема. Додавання векторів Мета уроку: формування вміння додавати вектори, вивчення властивостей суми векторів; формування вмінь застосовувати вивчені властивості й означення до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують додавання векторів; відкладають вектор, що дорівнює сумі векторів; формулюють […]...
- Координати вектора. Дії над векторами, що задані координатами 1. Запишемо координати вектора: 1) 2) 3) 4) 2. 1) 2) 3) 4) 5) 6) 3. 1) Запишемо розклад за координатними векторами: 2) Запишемо розклад за координатними векторами: 3) Запишемо розклад за координатними векторами: 4) Знайдемо координати векторів : Знайдемо координати вектора Запишемо розклад за координатними векторами: 5) Знайдемо координати векторів Знайдемо координати вектора Запишемо […]...
- Віднімання векторів УРОК № 45 Тема. Віднімання векторів Мета уроку: формування вмінь віднімати вектори, вивчення властивостей різниці векторів; формування вмінь застосовувати вивчені означення та властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині”[13]. Вимоги до рівня підготовки учнів: описують віднімання векторів; відкладають вектор, що дорівнює різниці векторів; формулюють властивості […]...
- Вектор. Модуль і напрям вектора. Рівність векторів УРОК № 42 Тема. Вектор. Модуль і напрям вектора. Рівність векторів Мета уроку: формування понять вектора, модуля вектора, напряму вектора; рівності векторів; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують вектор, модуль і […]...
- Множення вектора на число Геометрія Вектори Множення вектора на число Добутком вектораНа число називається вектор , тобто . Для будь-якого вектора і чисел і . Для будь-яких двох векторів і і числа . Теорема 1. Абсолютна величина вектора дорівнює . Напрям вектора , якщо , збігається з напрямом вектора , якщо , і протилежний напряму вектора , якщо . […]...
- Сума кутів трикутника Геометрія Основні властивості найпростіших геометричних фігур Сума кутів трикутника Теорема. Сума кутів трикутника дорівнює . Із цієї теореми випливають наслідки: 1. У будь-якому трикутнику принаймні два кути гострі (тобто в трикутнику не може бути більше одного прямого або тупого кута). 2. Кути рівностороннього трикутника дорівнюють . Зовнішнім кутом трикутника при даній вершині називається кут, суміжний […]...
- Алгебра векторів 1. Побудуємо вектори – одиничний вектор 2. Побудуємо вектори 3. Побудуємо вектори 4. Побудуємо вектори 5. 6. 1) Побудуємо вектори 2) Побудуємо вектори 7. Побудуємо вектори 8. 1) 2) 9. Побудуємо вектори Вектори та рівні. 10. Накреслимо два ненульові вектори Побудуємо Побудуємо Таким чином, 11. Побудуємо вектори Вектори протилежно напрямлені. 12. Побудуємо вектори 13. 1) […]...
- ВІДПОВІДІ ДО ТЕСТІВ ЕКСПРЕС-КОНТРОЛЮ ВІДПОВІДІ ДО ТЕСТІВ ЕКСПРЕС-КОНТРОЛЮ Тест 1. Тригонометричні функції кутів від 0° до 180° Варіант 1. 1. Б. 2. В. 3. Б. 4. 1. 5. 0. Варіант 2. 1. Б. 2. В. 3. В. 4. . 5. 0. Тест 2. Теорема косинусів та її наслідки Варіант 1. 1. В. 2. Б. 3. А. 4. 5 см. […]...
- Тригранний і многогранний кути Геометрія Многогранники Тригранний і многогранний кути Нехай промені a, b, c виходять з однієї точки й не лежать в одній площині. Тригранним кутом називається фігура, яка складається з трьох плоских кутів , , (див. рисунок). Ці кути називаються Гранями тригранного кута, а їх сторони – Ребрами. Спільна вершина плоских кутів називається Вершиною тригранного кута. Двогранні […]...
- Розкладання вектора за координатними осями Геометрія Вектори Розкладання вектора за координатними осями Вектор називається Одиничним, якщо його абсолютна величина дорівнює одиниці. Одиничні вектори, які мають напрями додатних координатних півосей, називаються Координатними векторами, або Ортами (див. рисунок). Позначення: ; . Оскільки координатні вектори відмінні від нуля й неколінеарні, то будь-який вектор можна розкласти за цими векторами: ....
- Кут між площинами Геометрія Стереометрія Кут між площинами Кут між паралельними площинами вважається таким, що дорівнює . Нехай дані площини перетинаються (див. рисунок). Проведемо площину, перпендикулярну до прямої їх перетину. Ця площина перетинає дані площини по двох прямих. Кут між цими прямими називається Кутом між даними площинами. Означений таким чином кут між площинами не залежить від вибору січної […]...
- Колінеарні вектори УРОК № 48 Тема. Колінеарні вектори Мета уроку: формування поняття “колінеарні вектори”; вивчення властивості та ознаки колінеарних векторів; формування вмінь учнів застосовувати вивчені означення та властивості до розв’язування завдань. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують колінеарність векторів; застосовують вивчені означення та […]...
- Многогранники Геометрія Многогранники Двогранним кутом називається фігура, утворена двома півплощинами зі спільною прямою, що їх обмежує, – ребром двогранного кута. Півплощини називаються Гранями двогранного кута. Площина, перпендикулярна до ребра двогранного кута, перетинає його грані по двох півпрямих. Кут, утворений такими півпрямими, називається Лінійним кутом двогранного кута (див. рисунок). За міру двогранного кута приймається міра його лінійного […]...
- Бісектриса Геометрія Основні властивості найпростіших геометричних фігур Бісектриса Бісектрисою кута називається промінь, який виходить із вершини кута, проходить між його сторонами й ділить кут пополам. На рисунку BD – бісектриса . Властивості бісектриси Теорема 1. Бісектриса кута утворює з його сторонами кути, не більші за . Теорема 2. Бісектриси вертикальних кутів лежать на одній прямій (тобто […]...
- Кути, вписані в коло Геометрія Кути, пов’язані з колом Кути, вписані в коло Кут розбиває площину на дві частини. Кожна із цих частин називається Плоским кутом. Плоскі кути із спільними сторонами називаються Доповняльними. Якщо плоский кут є частиною півплощини, то його градусною мірою називається градусна міра звичайного кута з тими самими сторонами. Центральним кутом у колі називається плоский кут […]...
- Формули суми (різниці) однойменних тригонометричних функцій. Перетворення добутку тригонометричних функцій у суму УРОК 15 Тема. Формули суми (різниці) однойменних тригонометричних функцій. Перетворення добутку тригонометричних функцій у суму Мета уроку: вивчення формул суми і різниці однойменних тригонометричних функцій і формул перетворення добутку тригонометричних функцій у суму. Формування умінь учнів застосовувати вивчені формули для спрощення виразів та обчислень. Обладнання. Таблиця “Формули перетворення суми в добуток (добутку в суму)”. І. […]...
- Множення вектора на число УРОК № 47 Тема. Множення вектора на число Мета уроку: формування вміння множити вектор на число; вивчення властивостей множення вектора на число; формування вмінь застосовувати вивчені значення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині”[13]. Вимоги до рівня підготовки учнів: описують множення вектора на число; […]...